ул.Симферопольская
дом 5, офис 9
Пн-Вс с 9:00 до 18:00
Корзина
Корзина пуста
4.2.Пример составления структурной схемы системы. Пример схемы структурной
Преобразование структурных схем. Граф системы управления.Соответствие структурных схем графам - математические основы теории автоматического управления
Правила структурных преобразований
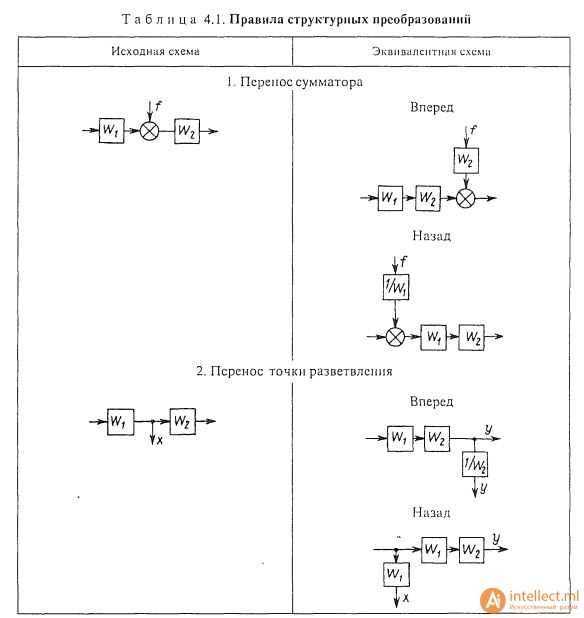
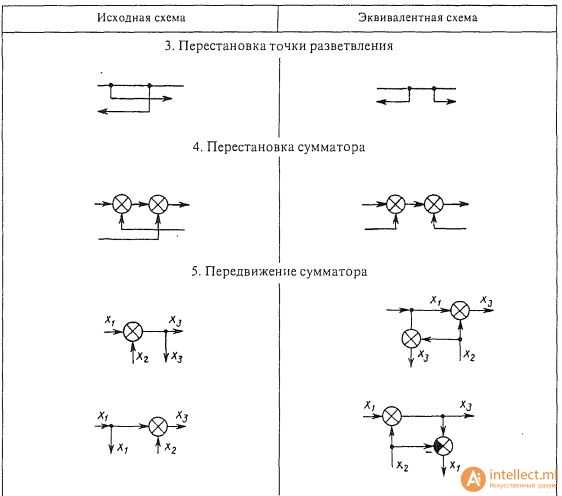
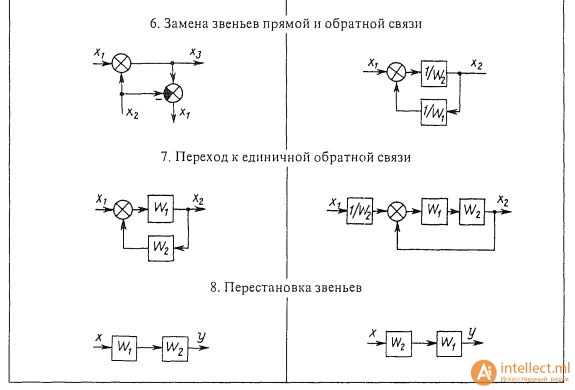
Последовательное соединение звеньев. При последовательном соединении звеньев (рис. 1.8, а) выходная величина предыдущего звена является входной величиной последующего звена. Передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:
Wc(p)=W1(p) * W2(p) * W3(p)
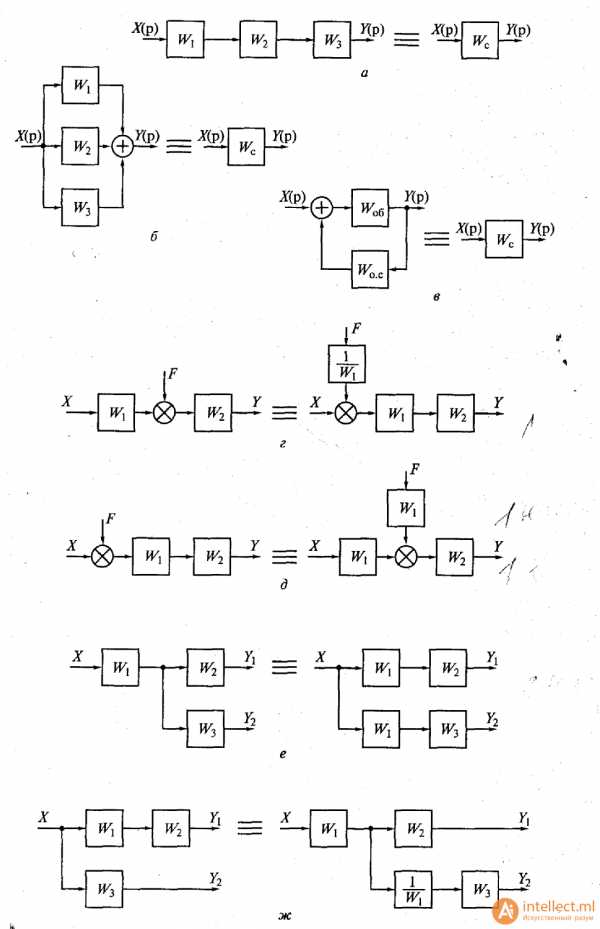
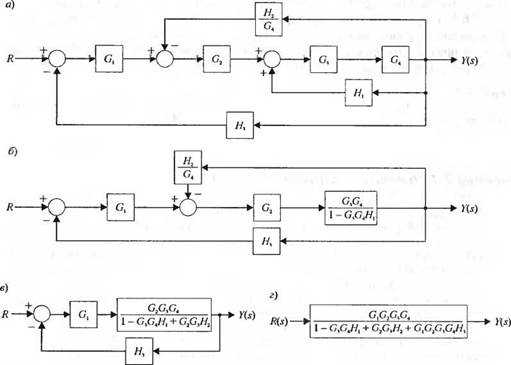
Рис. 1.8. Типы преобразований структурных схем:
а — преобразование передаточных функций последовательного включения трех звеньев в передаточную функцию одного эквивалентного звена; б — преобразование передаточных функций параллельного включения трех звеньев в передаточную функцию одного эквивалентного звена; в — преобразование передаточных функций встречно-параллельного включения двух звеньев в передаточную функцию одного звена; г — перемещение внешнего воздействия из середины схемы на вход; д — перемещение внешнего воздействия со входа в середину схемы; е — перемещение выходного сигнала из середины схемы на вход; ж — перемещение выходного сигнала со входа в середину схемыПараллельное соединение звеньев. Входная величина системы, состоящей из параллельно соединенных звеньев (рис. 1.8. б), одновременно подается на входы всех звеньев, а ее выходная величина равна сумме выходных величин отдельных звеньев. Передаточная функция системы, состоящей из параллельно соединенных звеньев, равна сумме передаточных функций этих звеньев:
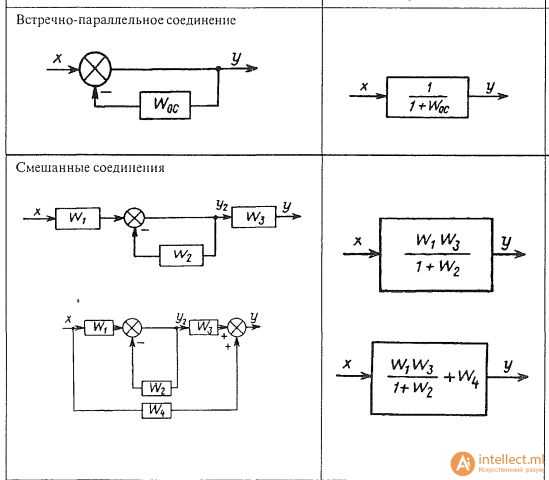
Wc(p)=W1(p) +W2(p)+ W3(p)Встречно-параллельное соединение звеньев. При встречно-па-раллельном соединении звеньев на вход соединения одновременно с входной величиной системы подается ее выходная величина, прошедшая через звено обратной связи с передаточной функцией Woc(р) (рис. 1.8, в). Передаточная функция системы определяется выражением:
Wc(p)=
В знаменателе знак «+» относится к отрицательной обратной связи, знак «-» — к положительной обратной связи. В промышленных системах в основном применяется отрицательная обратная связь.
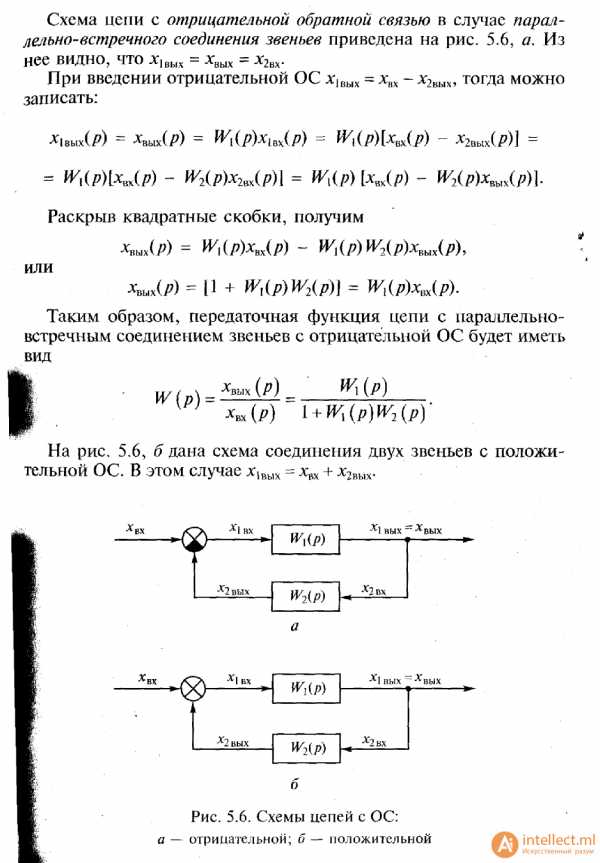
Схема цепи с отрицательной обратной связью в случае параллелъно-встречного соединения звеньев приведена на рис. 5.6, а. На рис. 5.6, б дана схема соединения двух звеньев с положительной ОС.
Таким образом, разбивка дифференциального уравнения, оп-ределяющего процесс автоматического управления в системе, на дифференциальные уравнения элементарных звеньев в общем случае может быть выполнена различными способами. Следовательно, один и тот же процесс управления может быть осуществлен с помощью систем, расчлененных на различное число элементарных звеньев с различными структурными связями между ними. Имея в качестве исходной какую-либо одну из таких систем и определив передаточные функции всех ее элементарных звеньев, можно в дальнейшем упростить структурную схему системы путем ее эквивалентных преобразований. Во всех различных струк-турных схемах, полученных в результате эквивалентных преобразований первоначальной схемы, передаточная функция системы в целом не изменяется и не зависит от того, на сколько и на какие элементарные звенья разделена система и какие структурные связи имеются между ее звеньями.
К уже приведенным преобразованиям структурных схем можно добавить следующие преобразования. Внешнее воздействие F, приложенное к выходу звена с передаточной функцией W1 (рис. 1.8, г), можно перенести на его вход, поместив между воздействием и входом звена дополнительное звено с передаточной функцией 1/W1. Внешнее воздействие F, приложенное ко входу звена с передаточной функцией W1, можно перевести на его выход (рис. 1.8, д), поместив между воздействием и выходом звена дополнительное звено с той же передаточной функцией W1. Точку присоединения любой структурной связи к выходу звена, имеющего передаточную функцию W1, можно перенести на его вход, включив в эту связь дополнительное звено с той же передаточной функцией W1(рис. 1.8, ё). Точку присоединения любой структурной связи ко входу звена с передаточной функцией W1 (рис. 1.8, ж) можно перевести на его выход, включив в эту связь дополнительное звено с передаточной функцией 1/W1.
С помощью перечисленных правил структурные схемы с пере-крестными связями можно преобразовать в структурные схемы без перекрестных связей, заменить многоконтурные автоматические системы управления одноконтурными, а также выделить линейную часть в нелинейных автоматических системах управления.
Эти правила лучше всего пояснить на примерах. На рис. 1.9, а показана исходная структурная схема системы, имеющая промежуточную связь. Эту систему можно преобразовать к виду, показанному на рис. 1.9, б, что позволяет использовать полученные ранее соотношения. Преобразованная структурная схема имеет две обратные связи, одна из которых, включающая звенья с передаточными функциями W3 и W 5, охватывает звено с передаточной функцией W 2, а вторая, состоящая из звеньев с передаточными функциями W3 и W4 образует главную обратную связь. Следовательно, звено с передаточной функцией W3вошло в структурную схему дважды. Применяя далее правила вычисления эквивалентных передаточных функций, приходим к простой структурной схеме одноконтурной системы автоматического регулирования (рис. 1.9, в), в прямой цепи которой находится звено с передаточной функцией
Wc=W1W2/(1-W2W3W5), (1-9)
а в цепи обратной связи
Woc=W3W4. (1-10)
Следует заметить, что при достаточном опыте можно установить наличие таких обратных связей без построения структурной схемы, показанной на рис. 1.9, б.
Преобразование структурных схем систем автоматического ре-гулирования, имеющих перекрестные обратные связи, приводит, как правило, к введению в преобразованную структурную схему звеньев с обратными передаточными функциями. Так, структурную схему системы с такими обратными связями (рис. 1.9, г) можно преобразовать к виду, показанному на рис. 1.9, д. Из этого рисунка видно, что главная обратная связь этой системы имеет звено с передаточной функцией 1/W1. После такого преобразования систему регулирования можно свести к одноконтурной (см. рис. 1.9, в). Передаточная функция звена в прямой цепи определяется как
W0=
а в цепи обратной связи
Woc=W5/W1.
Применение правил преобразования структурных схем систем автоматического регулирования и определения эквивалентных передаточных функций значительно упрощает анализ таких систем. Однако при экспериментальных исследованиях динамических систем часто возникает обратная задача — отыскание передаточной функции звена, когда известны передаточные функции системы в целом и остальных входящих в нее звеньев. Такая задача решается с помощью рассмотренных ранее правил.
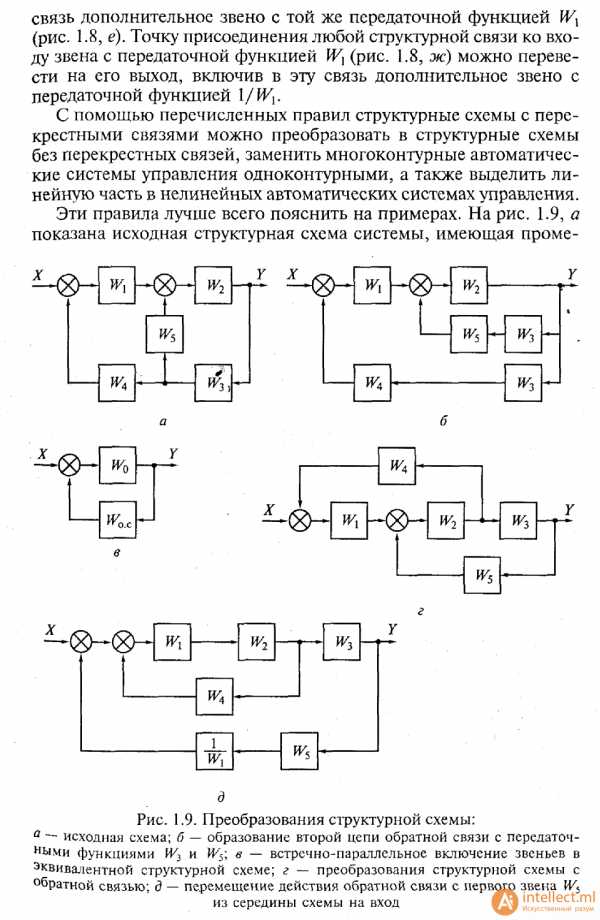
Рисунок 1.9. Преобразования структурной схемы
При параллельном встречном включении может иметь место частный случай Z(p)=1, передаточная функция системы для выходной величины:
Хвых(р)/Хвх(р)=W(p)/1+W(p),
Для ошибки: Х(р)/Хвх(р)=1/1+W(p).
Если W(p)=A(p)/B(p), то
для выходной величины Хвых(р)/Хвх(р)=A(p)/A(p)+B(p),
Для ошибки: Х(р)/Хвх(р)=В(р)/А(р)+B(p).
Сложные соединения звеньев. На рис. 1.10 изображена схема слож-ного соединения звеньев в САУ, на которой нетрудно увидеть типовые соединения. Первое и второе звенья здесь объединены в блок I с параллельно-согласованным соединением, пятое и шестое — в блок III с последовательным соединением. В блок II выделено четвертое звено, охваченное собственной положительной ОС. Условно можно принять, что в эту ОС включено пропорциональное звено с коэффициентом усиления, равным единице. Запишем передаточные функции выделенных блоков:
В свою очередь, блок I, третье звено и блок II соединены пос-ледовательно, а блок III включен в цепь отрицательной ОС. Используя приведенные ранее формулы, запишем передаточную функцию всей САУ:
Рисунок 1.10. Схема сложного соединения элементов САУ
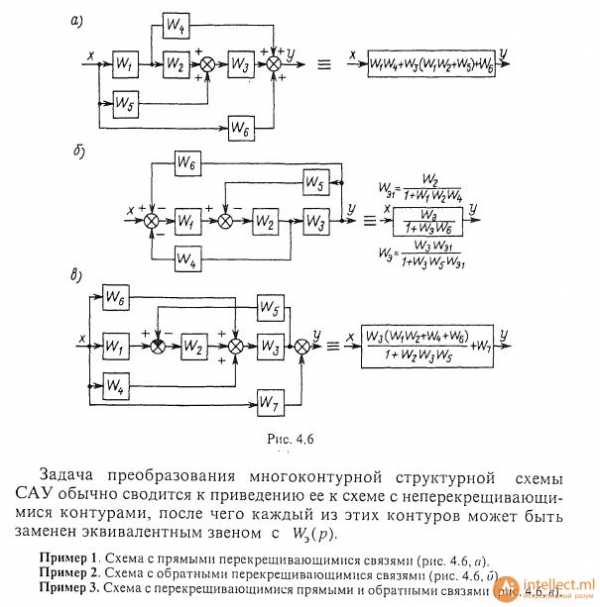
Задача преобразования многоконтурной структурной схемы САУ обычно сводится к приведению ее к схеме с неперекрещивающимися контурами, после чего каждый из этих контуров может быть заменен эквивалентным звеном с Wэ (р).
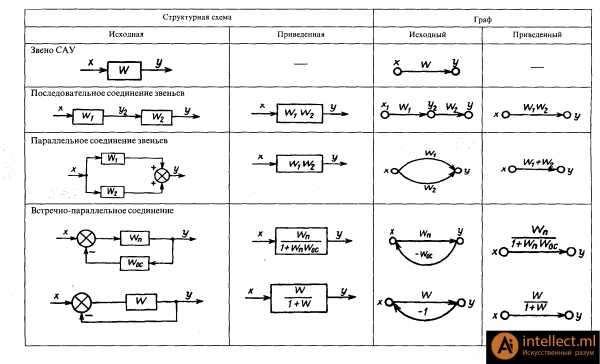
Передаточные функции сложных САУ можно определить по структурной схеме и без приведения ее к одноконтурной путем применения диаграмм прохождения сигналов (из теории графов). Графы прохождения сигналов подобны структурным схемам и также используются для наглядного изображения математических зависимостей в САУ (см. рис. 4.1). Направленный сигнальный (ориентированный) граф (указано направление сигнала) — более компактная форма записи структурных схем. Правила преобразования графов подобны правилам преобразования структурных схем (см. таблицу 1).
Граф представляет собой совокупность вершин (узлов), начала, конца и ребер. Ребро (ветвь, дуга) тождественно равно оператору W(р). Вершины графа — переменные (сигналы): у, и, х и т. д. В общем случае ребра — коэффициенты а, b, с, Ti, ki и т. д. в уравнениях САУ; дуга направленна и характеризуется символом k(W) (весом дуги).
Структурную схему САУ рассматривают как один из видов графа прохождения сигналов. Направленный (сигнальный) граф САУ строится по уравнениям, записанным, как и структурная схема САУ, в принятой условно-разрешенной форме.
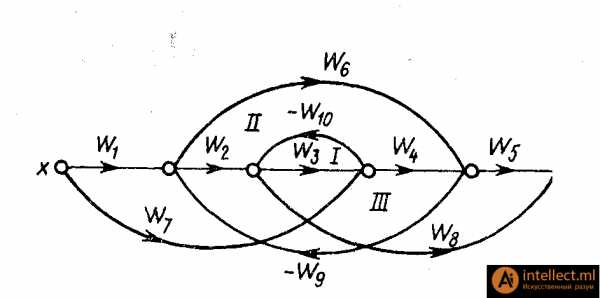
Таблица 1. Алгебра W(p). Соответствие структурных схем графам
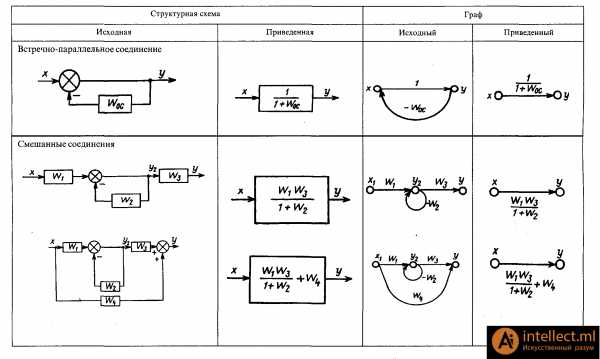
Пример математическая модель системы в виде структурной схемы соотвествующая заданному графу
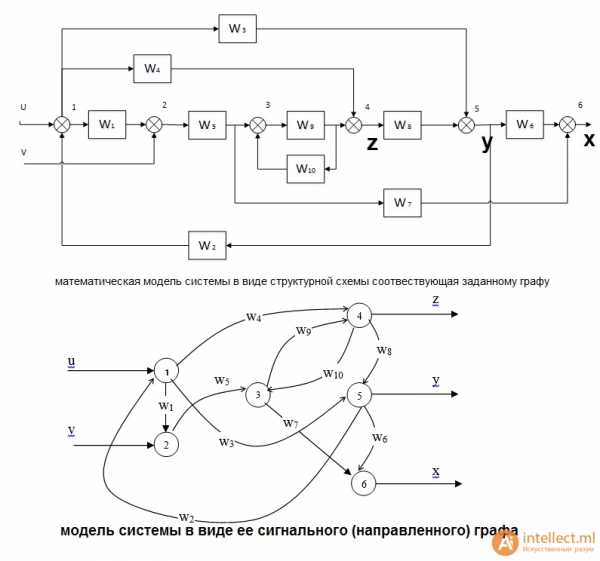
Задание 1. Преобразовать исходную структурную схему, определив передаточную функцию системы при условии .
Рис.1а
Рис.1.б
Задание 2. Преобразовать структурные схемы и определить передаточную функцию САУ.
Рисунок 3
Пример 1 Схема с прямыми перекрещивающимися связями (рис. 3,а).
Пример 2 Схема с обратными перекрещивающимися связями (рис. 3,б).
Пример 3 Схема с перекрещивающимися прямыми и обратными связями (рис. 3,в).
Задание 3. Сверните изображенную на рис. 4 структурную схему САУ и определите ОФП замкнутой системы по основному каналу и ОФП ошибки, если W1(p)=
W2(p)=
W3(p)=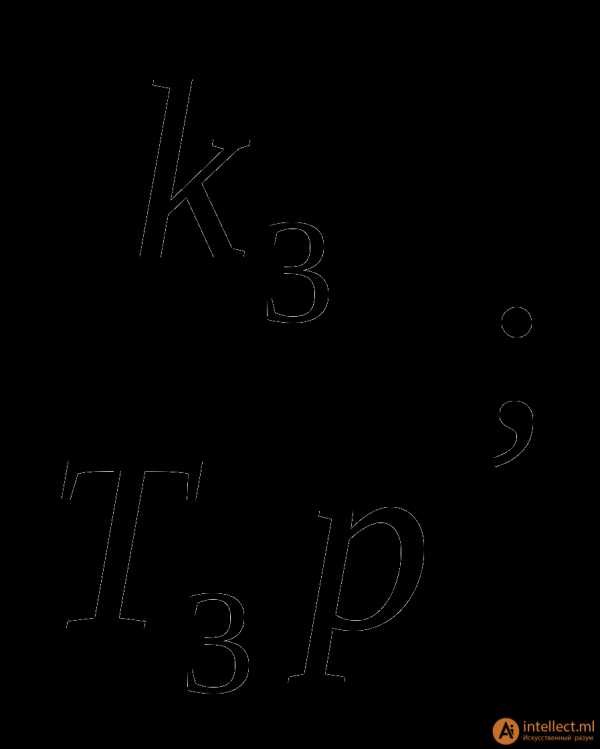
W4(p)=
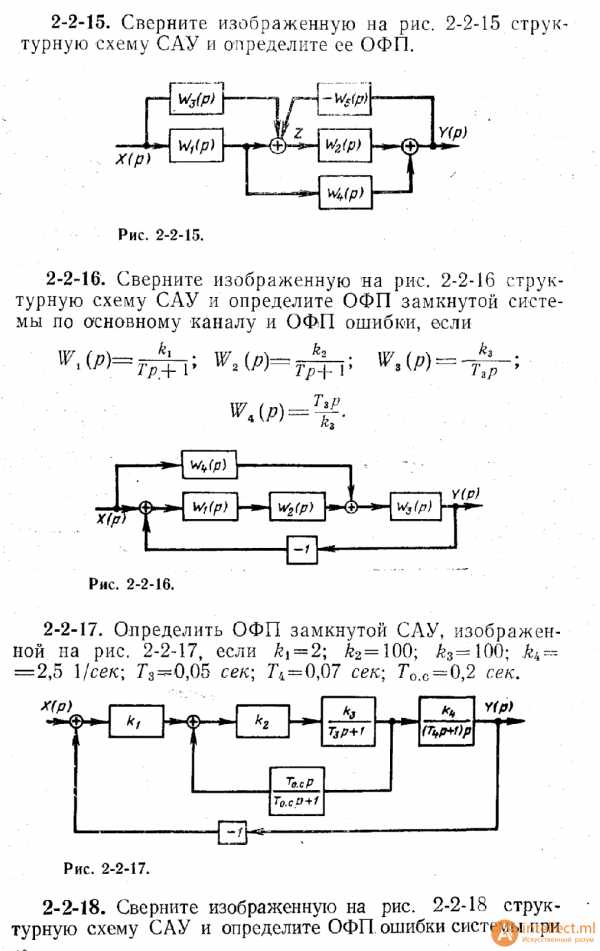
Рисунок 4
Задание 4.
Преобразуя структурную схему (рис. 5), получить в общем виде:
1) передаточную функцию разомкнутой системы;
2) передаточную функцию замкнутой системы для возмущающего воздействия;
3) передаточную функцию замкнутой системы для управляющего воздействия.
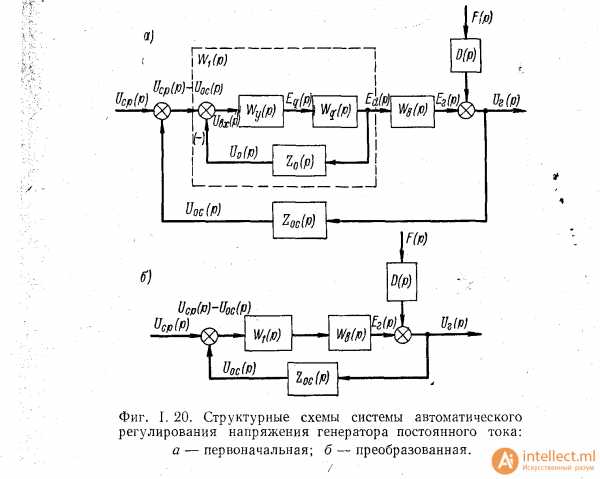
Рисунок 5.Задание 5.
На основании структурной схемы (рис. 6) получить в общем виде пере-даточные функции системы для выходной величины и ошибки.
Рисунок 6
Задание 6.
По заданной передаточной функции зарисовать структурную схему системы и граф системы управления по ее структурной схеме.Задание 7. На основании структурной схемы (рис. 7) получить в общем виде передаточную функцию замкнутой системы. Параметры системы: kс = 0,4 в/град; Тg= 0,06 сек.; Тм= 0,1 сек.; Се =0,014
; j = 297; kу2 = 5,2, Ку1=1,5, k0=3,2.
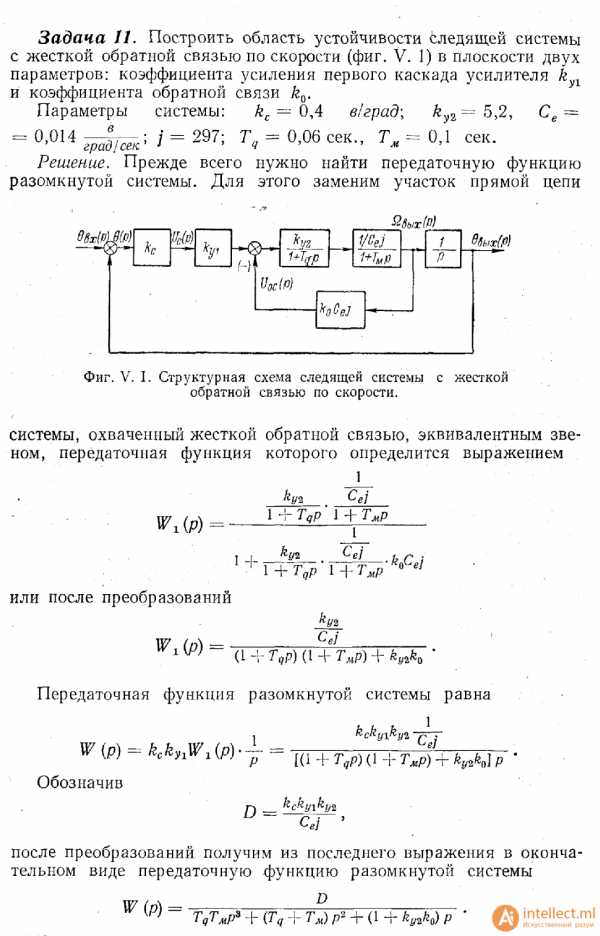
Рисунок 7
intellect.ml
Структурные схемы
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Динамические системы, в том числе и системы автоматического управления, на языке математики описываются системой обыкновенных дифференциальных уравнений. Как было отмечено в предыдущих разделах, использование преобразования Лапласа сводит задачу решения дифференциальных уравнений к решению системы линейных алгебраических уравнений. Поскольку в системах управления путем изменения одних переменных производится целенаправленное воздействие на другие переменные, то необходимо установить связь между этими переменными. Данную связь обычно представляют в виде передаточной функции, которая является одним из основных понятий теории управления.
Преимущество передаточной функции заключается в том, что она позволяет изобразить причинно-следственную связь между переменными в наглядной схематической форме. В теории управления преобладает представление различных динамических систем в
Рис. 2.22
Структурная схема двигателя постоянного тока
Рис. 2.23
Система с двумя входами и двумя выходами
виде структурных схем. Структурные схемы состоят из блоков направленного действия, каждому из которых соответствует определенная передаточная функция. Так, на рис. 2.22 изображена структурная схема двигателя постоянного тока, управляемого по цепи возбуждения, которая отражает связь между углом поворота 0(s) и приложенным напряжением Vf(s).
Для описания системы с несколькими управляемыми переменными используется структурная схема с перекрестными связями. Например, в системе на рис. 2.23 имеются две входных и две выходных переменных. С помощью передаточных функций мы можем записать связывающие их уравнения:
ВД = СИ(5)ВД + Gu(s)R2(s), (2.77)
У2(5) = G2l(s)Rx(s) + G22(s)R2(s), (2.78)
где G^s)—передаточная функция оту-го входа к У-му выходу. Структурная схема, отражающая записанные выше уравнения, представлена на рис. 2.24. В общем случае, при наличии./входов и/выходов, связывающие их уравнения можно записать в матричной форме:
| (4 | G, i (s) . | ■ Си(5) | R (s) | |
| ВД | = | 02i С*) ■ | ■ C2J(S) | R2(s) |
| ?! (*)- | G, x{s) | Gjj (s) | R, (s) |
или в компактном виде
Y = GR. (2.80)
Здесь У и R есть, соответственно, матрицы-столбцы, элементами которых являются 1 выходных и J входных переменных, a G — матричная передаточная функция размерности JxJ.
4F Подобное матричное представление имеет особую ценность при анализе много - связных (многомерных) систем управления. Для читателей, не знакомых с алгеброй матриц, основные сведения из этой области приводятся на Web-сайте MCS.
Рис. 2.24
Структурная схема системы с перекрестными связями
Пользуясь определенными правилами, структурную схему сложной системы можно упростить, сведя ее к конфигурации с меньшим числом блоков, чем в исходной системе. Поскольку передаточные функции являются средством описания линейных систем, им присуще свойство коммутативности. Следовательно, для поз. 1 из табл. 2.6 мы можем записать:
X3(s) = G2(s)X2(s) = С,(*)С2(4ад.
Если два блока соединены последовательно, то предыдущее уравнение можно записать также в виде
ВД = G2(s)Gl(s)A'l(s).
При этом предполагают, что если выход первого блока соединен со входом второго, то влияние нагрузки на первый блок является незначительным. Если же нагрузка оказывает существенное влияние на выходную переменную предшествующего блока, то инженер обязан учесть этот фактор и внести соответствующее изменение в передаточную функцию.
Таблица 2.6. Правила преобразования структурных схем
| Преобразование |
Исходная диаграмма Эквивалентная диаграмма
| 1. Последовательное соединение блоков |
| 2. Перенос сумматора через блок с передаточной функцией по ходу движения сигнала 3. Перенос узла через блок с передаточной функцией против движения сигнала |
4. Перенос узла через блок с передаточной функцией по ходу движения сигнала
с
5. Перенос сумматора через блок с передаточной функцией против движения сигнала
6. Исключение контура с обратной связью
Методы преобразования структурных схем основаны на рассмотрении алгебраических соотношений между отдельными переменными. Например, рассмотрим структурную схему, изображенную на рис. 2.25. В этой системе с отрицательной обратной связью сигнал на входе объекта управления записывается в виде :
£„(.s) = R(s) - B(s) = R(s) - n(s)Y(s). (2.81)
Поскольку выходная переменная связана с этим сигналом передаточной функцией C(.v), то
Y(s) = G(s)Ea(s) (2.82)
и, следовательно,
ад = едем - /адвд]. (2.83)
Группируя члены при Y(s), получим:
y(s)[l + С(5)Я(5)] = G(s)R(s). (2.84)
Отсюда получим передаточную функцию, связывающую выход со входом: Y(s)_ G(s)
(2.85)
R(s) 1+G(s)N(s)
Это выражение, известное как передаточная функция замкнутой системы, представляет особую ценность, т. к. оно свойственно большинству реальных систем управления. Сведение структурной схемы, представленной на рис. 2.25, к одному-единственному блоку является лишь одним примером элементарных преобразований, приведенных в табл. 2.6. Анализ систем путем преобразования структурных схем дает гораздо лучшее представление о роли каждого элемента, чем это было бы при рассмотрении уравнений. Правила преобразования структурных схем мы проиллюстрируем на примере сведения многоконтурной системы к более простому виду.
Рис. 2.25
Система с отрицательной обратной связью
Пример 2.7. Упрощение структурной схемы
На рис. 2.26 изображена структурная схема многоконтурной системы управления. Заметим, что сигнал Hx(s)Y(s) подается на сумматор со знаком плюс, поэтому контур, образованный блоками G3(s)Gt(s)Ht(s), называют контуром с положительной обратной связью. Упрощение этой структурной схемы основано на применении правила 6 из табл. 2.6, которое связано с исключением изолированных контуров. Поэтому необходимо будет использовать и другие правила, чтобы подготовить схему к применению правила 6. Сначала, чтобы исключить контур G3G4Hb мы перенесем узел через блок G4 по ходу движения сигнала (см. правило 4) и получим схему, изображенную на рис. 2.21(a). Исключая контур G3G4//| по правилу 6, мы получим схему рис. 2.21(6). Затем, исключая внутренний контур, содержащий Н2/С4, получим схему рис. 2.27(e). Наконец, исключая контур, содержащий Нъ, мы получим передаточную функцию замкнутой многоконтурной системы, как показано на рис. 2.21(г). Стоит обратить внимание на вид числителя и знаменателя этой передаточной функции. Можно видеть, что числитель образован произведением передаточных функций блоков, находящихся в прямой цепи от входа R(s) к выходу Y(s). Знаменатель равен единице минус сумма произведений передаточных функций блоков, образующих замкнутые контуры. Произведение G3G4Ht берется со
| Рис. 2.26. Многоконтурная система управления |
знаком плюс, поскольку это контур с положительной обратной связью, а произведения СОгСъС4Н3 и G2G3h3 — со знаком минус, т. к. в этих контурах обратная связь отрицательная. Чтобы лучше это проиллюстрировать, знаменатель можно записать в виде
= I — (+G3G4//] — GiGiHi — (і ] ОЧО'іОУ/з). (2.86)
Как мы увидим в следующем разделе, такой вид числителя и знаменателя характерен для многоконтурных систем управления.
|
Рис. 2.27. Упрощение структурной схемы системы рис. 2.24 |
Метод структурных схем широко распространен в теории и практике автоматического управления. Он дает очень наглядное графическое представление о взаимосвязи управляемых и входных переменных. Кроме того, проектировщик легко может обнаружить необходимость введения в существующую структурную схему дополнительных блоков с целью улучшения характеристик системы. Наряду со структурными схемами существует альтернативный метод представления модели систем в виде сигнального графа. Этот метод будет представлен в следующем разделе.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …
msd.com.ua
Структурное проектирование программ
В этом методе разбиение сложной системы на несколько подсистем получило название «разделяй и властвуй» (divide et impera), иерархическая или функциональная декомпозиция и др. При этом базовыми принципами являются:
a) «разделяй и властвуй»;
b) Проектирование «сверху вниз» - от общей постановки задачи к отдельным подзадачам и т.д.;
c) принцип иерархического упорядочения, который предполагает объединение составных частей системы в иерархические древовидные структуры с добавлением новых деталей на каждом уровне.
Процесс проектирования сложного программного обеспечения начинают с уточнения его структуры, т. е. определения структурных компонентов и связей между ними. Результат уточнения структуры может быть представлен в виде структурной и/или функциональной схем и описания (спецификаций) компонентов.
Структурная схема разрабатываемого программного обеспечения
Структурной называют схему, отражающую состав и взаимодействие по управлению частей разрабатываемого программного обеспечения. Обычно такие схемы разрабатывают для каждой программы большого пакета, а список программ определяют, анализируя функции, указанные в техническом задании.
Самый простой вид программного обеспечения - программа, которая в качестве структурных компонентов может включать только подпрограммы и библиотеки ресурсов. Разработку структурной схемы программы обычно выполняют методом пошаговой детализации.
Структурными компонентами программной системы или комплекса могут служить программы, подсистемы, базы данных, библиотеки ресурсов и т. п.
Так схема программного комплекса демонстрирует передачу управления от программы-диспетчера соответствующей программе, как показано на рис. 4.1. Программы комплекса, как правило, слабо связаны. Поэтому для организации их совместной работы используется диспетчер.
Рис. 4.1. Пример структурной схемы программного комплекса.
Структурная схема программной системы, как правило, показывает наличие подсистем или других структурных компонентов. В отличие от комплекса отдельные части (подсистемы) программной системы интенсивно обмениваются данными между собой и, возможно, с основной программой. Структурная же схема программной системы этого, как правило, не показывает, как это видно из рис. 4.2.
Рис. 4.2
Обычно она представляет собой многоуровневую иерархическую схему взаимодействия подпрограмм по управлению. На начальном этапе схема отображает два уровня иерархии, т. е. показывает общую структуру программы. Однако тот же метод позволяет получить структурные схемы с большим количеством уровней.
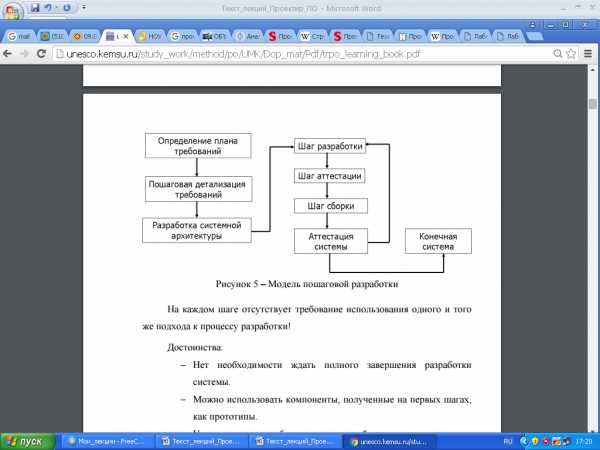Метод пошаговой детализации реализует нисходящий подход и базируется на основных конструкциях структурного программирования. Он предполагает пошаговую разработку алгоритма, как показано на рисунке 4.3. Каждый шаг при этом включает разложение функции на подфункции. Так на первом этапе описывают решение поставленной задачи, выделяя общие подзадачи. На следующем аналогично описывают подзадачи, формулируя при этом элементы следующего уровня. Таким образом, на каждом шаге происходит уточнение функций проектируемого программного обеспечения. Процесс продолжают, пока не доходят до подзадач, алгоритмы, решения которых очевидны.
Рис. 4.3
При этом необходимо, в первую очередь, детализировать управляющие процессы, оставляя уточнение операций с данными напоследок. Это связано с тем, что приоритетная детализация управляющих процессов существенно упрощает структуру компонентов всех уровней иерархии и позволяет не отделять процесс принятия решения от его выполнения. Определив условие выбора некоторой альтернативы, сразу же вызывают модуль, ее реализующий.
Функциональная схема или схема данных (ГОСТ 19. 701-90) - схема взаимодействия компонентов программного обеспечения с описанием информационных потоков, состава данных в потоках и указанием используемых файлов и устройств. Для изображения этих схем используют специальные обозначения, установленные стандартом.
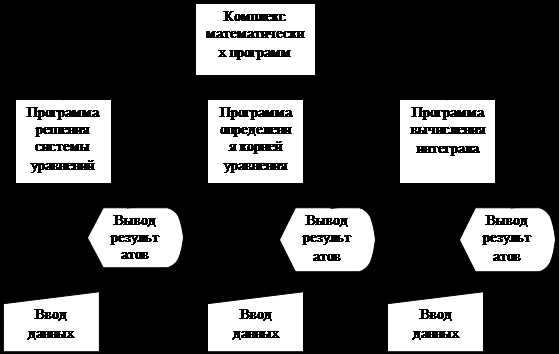
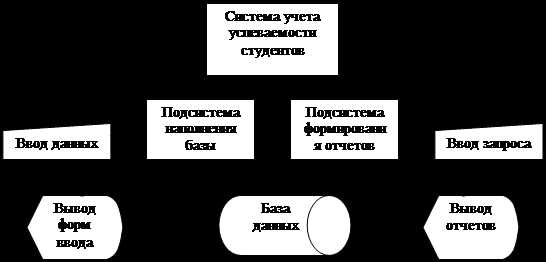
Функциональные схемы более информативны, чем структурные. На рис. 4.4 для сравнения приведены функциональные схемы программных комплексов и систем.
а)
б)
Рис. 4.4. Примеры функциональных схем: а - комплекс программ, б - программная система.
Все компоненты структурных и функциональных схем должны быть описаны. При структурном подходе особенно тщательно необходимо прорабатывать спецификации межпрограммных интерфейсов, так как от них зависят самые дорогостоящие ошибки.
Структурное проектирование использует три основных вида моделей (диаграмм):
1) SADT (Structured Analysis and Design Technique — метод структурного анализа и проектирования) — модели и соответствующие функциональные диаграммы;
2) DFD (Data Flow Diagrams) - диаграммы потоков данных;
3) ERD (Entity-Relationship Diagrams) — диаграммы «сущность-связь».
Функциональная модель SADT отображает функциональную структуру объекта, т.е. производимые им действия и связи между этими действиями.
Главным компонентом модели является диаграмма. На ней все функции и интерфейсы представлены в виде блоков и дуг соответственно. Место соединения дуги с блоком определяет тип интерфейса. Управляющая информация входит в блок сверху. Входная информация, которая подвергается обработке, показана с левой стороны блока, а результат (выход) - с правой. Механизм (человек или автоматизированная система), который осуществляет операцию, представляется дугой, входящей в блок снизу (рис. 4.5).
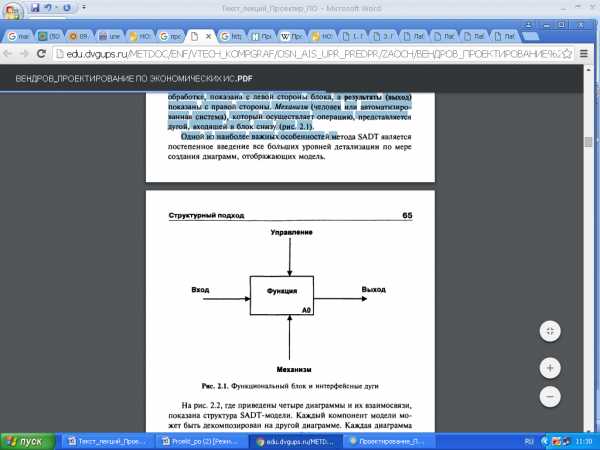
Рис.4.5
Построение SADT-модели начинается с представления всей системы в виде простейшего компонента — одного блока и дуг, изображающих интерфейс с функциями вне системы. Затем этот блок детализируется на другой диаграмме с помощью нескольких блоков, соединенных интерфейсным дугами. Новые блоки определяют основные подфункции исходной функции, которые, в свою очередь, могут быть детализировании и т.д. (см. рис. 4.6).
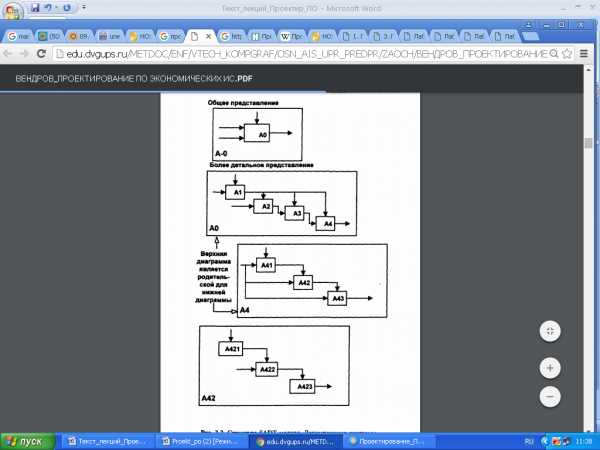Рис. 4.6
Диаграммы потоков данных (DFD) являются основным средством моделирования функциональных требований к проектируемой системе. С их помощью эти требования представляются в вид иерархий функциональных компонентов (процессов), связанных потоками данных. Главная цель такого представления — продемонстрировать, как каждый процесс преобразует свои входные данные в выходные, а также выявить отношения между этими процессами.
Основными компонентами диаграмм потоков данных являются:
a) внешние сущности;
b) системы и подсистемы;
c) процессы;
d) накопители данных;
e) поток данных.
Внешняя сущность представляет собой материальный объект или физическое лицо, являющийся источником или приемником информации. Она изображается объемным прямоугольником с надписью, как показано на рисунке 4.7.
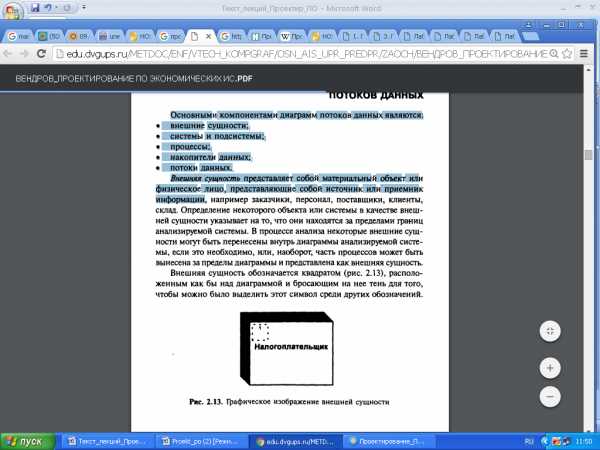
Рис. 4.7
Подсистема (см. рис. 4.8) или процесс (рис. 4.9) представляются прямоугольником с закругленными краями. Он содержит три поля:
a) Номера;
b) Имени;
c) Физической реализации.
Подсистема и процесс отличаются именем. В первой записывается название подсистемы, а во втором – глагол, определяющий, что делает процесс.
Рис. 4.8. ГНИ – Государственная налоговая инспекция
Рис. 4.9
Накопитель данных - это абстрактное устройство для хранения информации. Он изображается, как показано на рис. 4.10. Его обозначение начинается с буквы D.
Рис. 4.10
Поток данных на диаграмме изображается линией, оканчивающейся стрелкой, которая показывает направление потока. Каждый поток данных имеет имя, отражающее его содержание.
Пример диаграммы потоков данных приведен на рис. 4.11.
Более сложная диаграмма потоков данных приведена на рис. 4.12.
ER-диаграммы будут рассмотрены позднее.
В курсовом проекте, кроме функциональной диаграммы, необходимо представить схемы алгоритмов наиболее сложных функций (например, сортировки и поиска).
Рис. 4.11
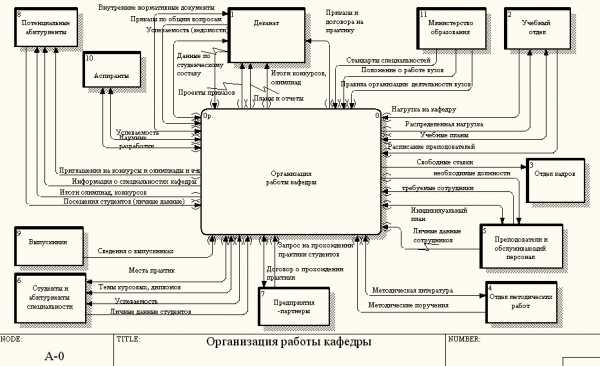
Рис. 4.12
Похожие статьи:
poznayka.org
Пример выполнения структурной схемы
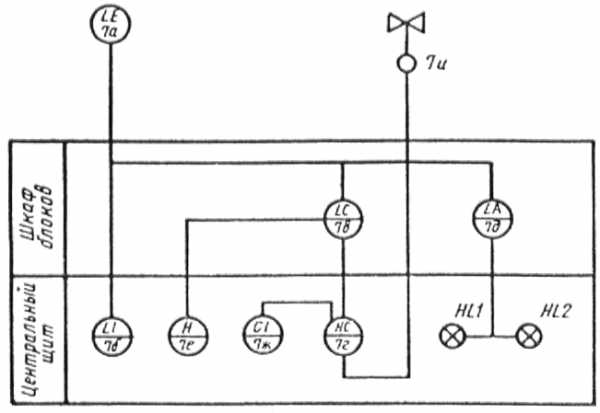
Рисунок 4
4.3.7.5Пример выполнения схемы автоматизации упрощенным способом приведен в приложении В.
4.4 Схемы принципиальные
4.4.1В зависимости от назначения и применяемых средств автоматизации разрабатывают:
— принципиальные электрические и пневматические схемы контуров контроля регулирования и управления;
— принципиальные схемы питания.
Принципиальные электрические схемы управления электроприводами оборудования и трубопроводной арматуры включают в состав основного комплекта при управлении ими со щитов и пультов систем автоматизации.
Принципиальные схемы контуров контроля и регулирования допускается не разрабатывать, если взаимные связи приборов и аппаратов, входящих в них, просты и однозначны и могут быть показаны на других чертежах основного комплекта. Допускается совмещение схем различного функционального назначения (например, схемы питания со схемой управления) с соблюдением правил выполнения этих схем, приведенных ниже.
4.4.2Электрические схемы выполняют по ГОСТ 2.701и ГОСТ2.702.На электрических схемах допускается:
— не приводить обозначения выводов электроаппаратов, если они приведены в технической документации на щиты и пульты;
— не включать в обозначение элементов квалифицирующие символы.
4.4.3Схемы с применением комбинированных средств автоматики (пневматических и электрических) выполняют по ГОСТ 2.701.
4.4.4На принципиальных схемах данные о технических средствах записывают в перечень элементов по ГОСТ 2.701.
Допускается в перечень элементов записывать аппаратуру группами соответственно местам их установки. Этим группам присваивают заголовки и указывают их в графе «Наименование».
Пример —«Аппараты по месту», «Щит управления» и т. п.
4.4.5На пневматических схемах контуров контроля и управления показывают:
— приборы, входящие в состав контуров;
— пневматические командные линии связи и линии пневмопитания;
— линии подвода электропитания.
Импульсные линии связи, подводящие измеряемые и регулируемые среды к датчикам, измерительным приборам и регуляторам на пневматических схемах не изображают.
4.4.6Приборы (за исключением исполнительных механизмов и регулирующих органов, изображаемых по ГОСТ 21.404)показывают упрощенно в виде прямоугольников. При этом показывают:
— в кружках, располагаемых по контуру прямоугольника — обозначения входных и выходных присоединений приборов (штуцеров) для подключения командных линий связи и питания, установленных в технической документации на прибор, или на соответствующей схеме;
— внутри прямоугольника —буквенно-цифровое обозначение прибора.
4.4.7Обозначения присоединительных штуцеров наиболее распространенных приборов приведены в таблице 1.
Таблица 1
| Обозначение штуцера | Назначение |
| 1 | Программа |
| 2 | Выход |
| 3 | Вход (переменная) |
| 4 | К включающему реле регулирующего устройства |
| 5 | питания сжатым воздухом |
| 6 | Задание |
| 7 | К исполнительному механизму |
Если прибор имеет несколько присоединительных штуцеров одного назначения, то в их обозначение через дефис включают порядковый номер.
Пример — 2-1, 2-2, 2-3;
4.4.8Обозначение прибора состоит из буквенного обозначения, соответствующего функциональному назначению прибора, и его порядкового номера.
Пример —РУ1, РУ2, Ф1, Ф2.
Буквенные обозначения наиболее распространенных приборов и элементов пневмоавтоматики принимают по таблице 2.
Таблица 2
| Наименование | Обозначение |
| Датчик | Д |
| Вторичный измерительный прибор | ВИП |
| Измерительный механизм показывающий | ИМ-П |
| Измерительный механизм самопишущий | ИМ-С |
| Измерительное устройство | ИУ |
| Ручной задатчик | РЗ |
| Станция управления | СУ |
| Программный задатчик | ПЗ |
| Регулирующее устройство | РУ |
| Регулирующее устройство соотношения | РУС |
| Кнопки переключающих устройств и станций управления: — ручное дистанционное управление | Р |
| — автоматическое управление | А |
| — программное регулирование | АП |
| — регулятор включен | Вкл. |
| — регулятор отключен | Откл. |
| Усилитель мощности | УМ |
| Устройство алгебраического суммирования | УС |
| Устройство предварения | УП |
| Устройство умножения на постоянный коэффициент | УУ |
| Блок ограничения сигнала | БО |
| Пневматический сигнализатор | ПС |
| Пневмотабло | ПТ |
| Реле переключения | РП |
| Панель управления | ПУ |
| Исполнительный механизм | ИМ |
| Позиционер | П |
| Манометр контрольный | МН |
| Фильтр воздуха | Ф |
| Стабилизатор (редуктор) давления воздуха | СД |
| Вентиль запорный | ВН |
| Кран трехходовой | К |
4.4.9Станции управления и отдельные переключающие устройства выполняют упрощенно, в развернутом виде, в выбранном рабочем положении (ручном, автоматическом и др.) с указанием режима, для которого приведены элементы переключающих устройств.
Регулирующие органы показывают на схемах в случаях, если они являются общими с исполнительными механизмами.
4.4.10Линии связи на пневматических схемах выполняют сплошными тонкими линиями, линии электропитания—штрихпунктирными тонкими линиями. Стрелками указывают направление пневматического сигнала. Линии питания сжатым воздухом, электропитания и сброс воздуха в атмосферу допускается наносить по рисунку 5.
|
| линия питания сжатым воздухом |
|
| сброс в атмосферу |
|
| линия электропитания |
Рисунок 5
4.4.11На пневматических схемах питания показывают:
— главный и распределительные коллекторы;
— сети воздуховодов от коллекторов до пневмоприемников;
— стабилизаторы давления воздуха и фильтры;
— контрольные манометры;
— запорную арматуру;
— резервные и продувочные вентили;
— воздухосборники (при необходимости).
На схемах питания воздуховоды не нумеруют и пневмоприемники не изображают. При этом, в нижней части схемы приводят таблицу с характеристикой пневмоприемников (позиционные обозначения в соответствии со схемой автоматизации, типы, расход сжатого воздуха, места установки).
4.4.12Условные графические обозначения, применяемые на схемах питания, принимают по следующим стандартам:
— фильтры воздуха ............................................... по ГОСТ 2.793
— стабилизаторы давления воздуха ................... по ГОСТ 2.785
— вентили запорные, краны трехходовые .......... по ГОСТ 2.785
— манометры контрольные .................................. по ГОСТ 2.781
— трубопроводы сжатого воздуха ....................... по ГОСТ 2.784
4.4.13На схемах пневмопитания указывают диаметры условных проходов труб коллекторов и ответвлений воздухопроводов к пневмоприемникам. Над линией, изображающей коллектор, указывают давление, под линией —расход сжатого воздуха.
4.4.14В перечне элементов к пневматическим схемам, указывают:
— в графе «Поз. обозначение» —обозначение прибора по 4.4.8;
— в графе «Наименование» —наименование прибора и его тип;
— в графе «Примечание» —обозначения приборов, указанные на схемах автоматизации.
Пример выполнения перечня элементов приведен на рисунке 6.
| Поз. обозначение | Наименование | Кол. | Примечание |
| Аппараты по месту | |||
| Д1, Д2 | Ротаметр пневматический РП-16ЖУЗ | 2 | 44б, 45а |
| ИМ | Клапан регулирующий фланцевый | 1 | 44д |
| 25ч37нж | |||
| Щит управления | |||
| ВИП | Прибор контроля пневматический. | 1 | 44в |
| показывающий ПКП.2 | |||
| РУ | Устройство регулирующее пневматическое пропорционально-интегральное | 1 | 45г |
| ПРЗ.31М1 |
Рисунок 6
4.4.15.Примеры выполнения принципиальных пневматических схем приведены в приложениях Г и Д.
studfiles.net
4.2.Пример составления структурной схемы системы
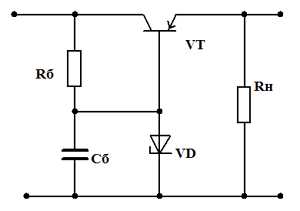
В качестве примера рассмотрим составление структурной схемы двигателя постоянного тока независимого возбуждения, как объекта регулирования. Электрическая схема двигателя представлена на рис. 4.3.
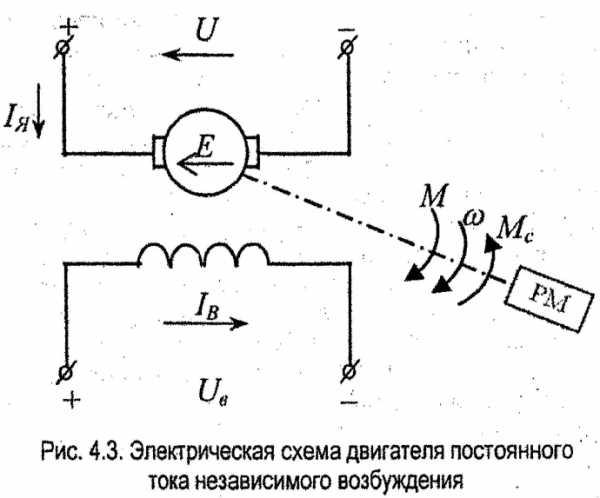
Представим основные уравнения для двигателя независимого возбуждения, полагая, что магнитный поток двигателя Ф=const.
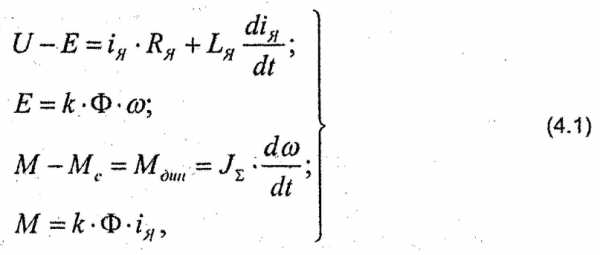
где U,E - соответственно напряжение и ЭДС двигателя;
iя, М - ток якоря и момент двигателя;
Rя, Lя - активное сопротивление и индуктивность обмотки якоря двигателя;
Uв,Iв- напряжение и ток возбуждения двигателя.
Запишем уравнения (4.1) в операторном виде.
Для якорной цепи как динамического звена можно получить следующую передаточную функцию, позволяющую получить структурную схему звена (рис. 4.4):
где TЯ=LЯ/RЯ - электромагнитная постоянная времени двигателя.
Аналогично можно представить структурные схемы других звеньев по их передаточным функциям
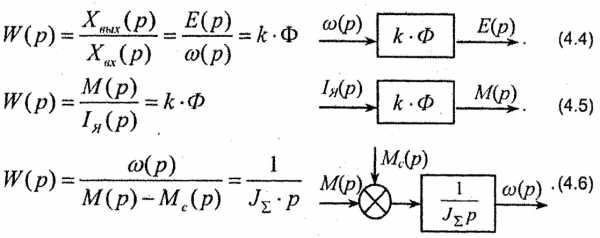
По структурным схемам отдельных звеньев может быть получена полная структурная схема двигателя независимого возбуждения как объекта регулирования (рис. 4.5).
4.3. Получение передаточной функции разомкнутой системы по передаточным функциям звеньев
Дифференциальное уравнение всей системы может быть получено из уравнений отдельных звеньев, если исключить из них обычным порядком все промежуточные переменные и оставить только входное воздействие и выходную переменную. Но значительно более просто можно получить описание системы, если оперировать передаточными функциями звеньев. Различают следующие способы соединения звеньев:
1) последовательное, при котором выходная величина предыдущего звена является входной для последующего звена;
2) параллельное, при котором на вход нескольких звеньев подается одна и та же величина, а выходная величина представляет собой сумму выходных величин этих звеньев;
3) замыкание системы или нескольких звеньев обратной связью, когда на вход замыкаемых звеньев с их выхода подается сигнал через замыкающие звенья, находящиеся в цепи обратной связи.
4.3.1.Передаточная функция цепи последовательно соединенных звеньев направленного действия
Предположим, что система состоит из n-последовательно включенных звеньев. В этом случаи можно записать следующую систему уравнений для них:
Из уравнений следует, что выходная величина первого звена является входной величиной второго звена и т.д.
Для того, чтобы выразить зависимость между выходной величиной системы Хвых и входной величиной Хвх нужно исключить все промежуточные переменные Хвых1, Хвых2 и т.д. Для этого первое уравнение нужно подставить во второе, затем полученное уравнение подставить в третье и т.д.
После исключения промежуточных переменных получим:
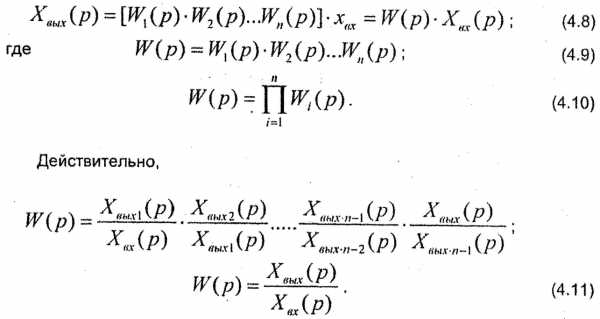
Следовательно, передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций звеньев. Отсюда следует, что такую цепь можно заменить в структурной схеме одним эквивалентным звеном с передаточной функцией W(p).
4.3.2. Параллельное соединение звеньев направленного действия (рис. 4.6)
Для параллельного включения звеньев можно записать следующую систему уравнений:
Следовательно, входной величиной всех параллельно соединенных звеньев является одна и та же величина Хвх. Выходные величины для каждого звена различны, они зависят от динамических свойств звеньев, а значит, от вида передаточных функций. Общая выходная величина всей системы Хвых представляет собой алгебраическую сумму выходных величин отдельных звеньев.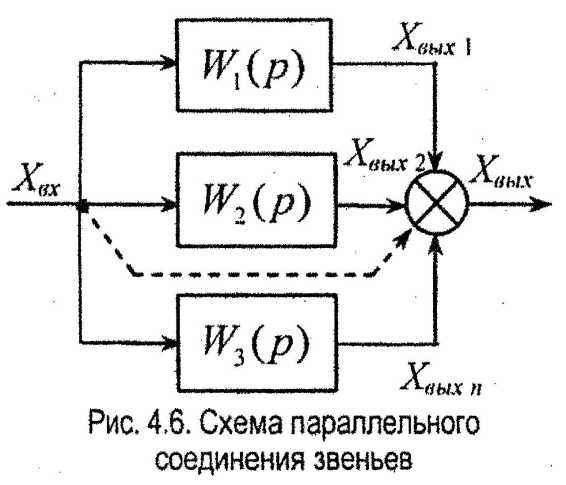
. (4.13)
Сложив левые и правые части уравнения (4.12), получим
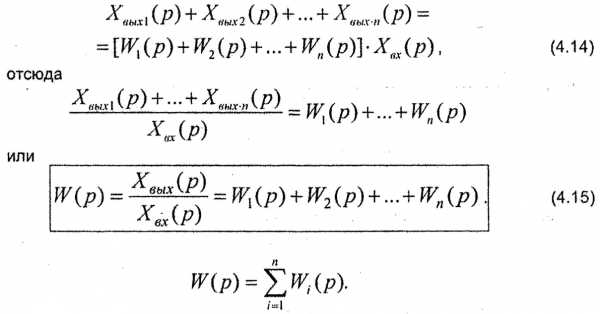
Следовательно, передаточная функция группы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.
studfiles.net
Структурные схемы примеры
 |
wwogoj.kl.com.ua
Карта сайта
г.Краснодар, ул.Симферопольская дом 5, офис 9
8 (989) 212 27 02 
8 (861) 260 24 40
