Онлайн журнал электрика. Закон ома выражается формулой

Ответы@Mail.Ru: 3 закона ома

Перейти к: навигация, поиск Просмотр этого шаблона Классическая электродинамика Solenoid.svg Электричество · Магнетизм [показать] Электростатика [показать] Магнитостатика [показать] Электродинамика [показать] Электрическая цепь [показать] Ковариантная формулировка [показать] Известные учёные См. также: Портал: Физика V — напряжение, I — сила тока, R — сопротивление. Зако́н О́ма — физический закон, определяющий связь между электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома. В своей оригинальной форме он был записан его автором в виде : X\! = {a \over {b+l}} (1), Здесь X — показания гальванометра, т. е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) \varepsilon\!, l — величина, определяемая длиной соединяющих проводов. Чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1]. В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает Закон Ома для полной цепи: I\! = {\varepsilon\! \over {R+r}}, (2) где: {\varepsilon\!} — ЭДС источника напряжения (В) , I\! — сила тока в цепи (А) , R\! — сопротивление всех внешних элементов цепи (Ом) , r\! — внутреннее сопротивление источника напряжения (Ом) . Из закона Ома для полной цепи вытекают следствия: При r<<r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока. Часто [2] выражение: U\! = IR (3) (где U\! есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома» . Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется: {\varepsilon\!} = Ir + IR = U(r) + U (R) (4) То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах» , поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС. К другой записи формулы (3), а именно: I\! = {U \over R}, (5) Применима другая формулировка: « Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. » Выражение (5) можно переписать в виде: I\! = {U G}, (6) где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо [3], впоследствии переименованный в Си́менс (обозначение: См, S).

touch.otvet.mail.ru

Закон Ома для активного и пассивного участка линейной электрической цепи

Закон Ома для пассивного участка электрической цепи.

При протекании электрического тока через сопротивление R, напряжение U и ток I на этом участке связаны между собою согласно закону Ома:

Сопротивление R - это коэффициент пропорциональности между током и напряжением. Чтобы найти сопротивление, нужно напряжение на участке электрической цепи разделить на ток, протекающий на этом же участке.

Закон Ома можно записать через разность потенциалов:

Закон Ома для активного участка электрической цепи.

Закон Ома для активного участка цепи между точками а и в имеет вид:

Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.

Пример составления уравнения по закону Ома

Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.

Пусть в данной электрической цепи направление тока будет из точки "a" в точку "b". Напряжение Uab Направляется всегда из первой буквы ("a") к последней ("b").

Согласно правилу составления уравнения по закону Ома источник ЭДС E1 берем со знаком "плюс", т.к. его направление (направление стрелочки) совпадает с направлением протекающего тока.

Источник ЭДС E2 берем со знаком "минус", т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.

Напряжение Uab или разность потенциалов φa - φb берем со знаком "плюс", т.к. его направление совпадает с направление протекающего тока.

Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.

В результате составленное уравнение по закону Ома будет иметь вид:

Пусть потенциал в данной задаче потенциал точки "а" равен 10 вольт, потенциал точки "b" = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:

Полученный ток равен 1 Ампер.

www.kurstoe.ru

Закон Ома | Онлайн журнал электрика

Диаграмма – Закон Ома.

На рис. показана схема знакомой вам простейшей электронной цепи. Эта замкнутая цепь состоит из 3-х частей: источника напряжения – батареи GB, потребителя тока – нагрузки R, которой может быть, к примеру, нить накала электронной лампы либо резистор, и проводников, соединяющих источник напряжения с нагрузкой. Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.

Простая электронная цепь неизменного тока.

Нагрузка R, владеющая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи находится в зависимости от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем огромным ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается последующей формулой: I = U/R,где I – ток, выраженный в амперах, А; U – напряжение в вольтах, В; R – сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и назад пропорционален его сопротивлению. Это основной закон электротехники, называемый законом Ома (по фамилии Г. Ома), для участка электронной цепи. Используя закон Ома, можно по двум известным электронным величинам выяснить неведомую третью. Вот несколько примеров практического внедрения закона Ома.

1-ый пример: На участке цепи, владеющем сопротивлением 5 Ом, действует напряжение 25 В. Нужно выяснить значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.2-ой пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Сначала ток 20 мА необходимо выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.

3-ий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Тут, как и в прошлом примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Как следует, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем молвят эти сведения? О том, что лампочка будет нормально сиять при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, несложно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити существенно меньше. Закон Ома справедлив не только лишь для участка, да и для всей электронной цепи. В данном случае в значение R подставляется суммарное сопротивление всех частей цепи, в том числе и внутреннее сопротивление источника тока. Но при простых расчетах цепей обычно третируют сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим приведу очередной пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Приблизительно таковой ток потребляет электронный паяльничек.

Всеми этими формулами, вытекающими из закона Ома, можно воспользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы, довольно просто уяснить, если воспользоваться вот этой графической схемой, т. н. треугольник закона Ома:

Воспользоваться этим треугольником просто, довольно верно уяснить, что горизонтальная линия в треугольнике значит символ деления (по аналогии дробной черты), а вертикальная линия в треугольнике значит символ умножения.

Сейчас разглядим таковой вопрос: как оказывает влияние на ток резистор, включаемый в цепь поочередно с нагрузкой либо параллельно ей? Разберем таковой пример. У нас имеется лампочка от круглого электронного, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, изначальное напряжение которой 4,5 В? Несложно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежайшей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, практически в два раза превосходящий тот ток, на который она рассчитана. Таковой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все таки можно питать от батареи 336Л, если поочередно в цепь включить дополнительный резистор сопротивлением 25 Ом, как это показано на рис..

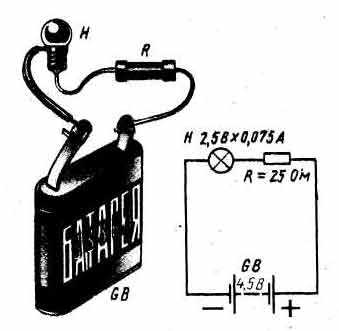Дополнительный резистор, включенный в цепь, ограничивает ток в этой цепи.

В данном случае общее сопротивление наружной цепи будет равно приблизительно 55 Ом, т.е. 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление дополнительного резистора R. В цепи, как следует, потечет ток, равный приблизительно 0,08 А, т.е. практически таковой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высочайшим напряжением и даже от электроосветительной сети, если подобрать резистор соответственного сопротивления. В этом примере дополнительный резистор ограничивает ток в цепи до подходящего нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В этом случае в цепь было включено поочередно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при поочередном соединении сопротивлений ток схож во всех точках цепи. Можно включать амперметр в всякую точку цепи, и везде он будет демонстрировать одно значение. Это явление можно сопоставить с потоком воды в реке. Русло реки на разных участках может быть широким либо узеньким, глубочайшим либо маленьким. Но за определенный просвет времени через поперечное сечение хоть какого участка русла реки всегда проходит однообразное количество воды.

Дополнительный резистор, включаемый в цепь поочередно с нагрузкой (как, к примеру, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится дополнительным резистором либо, как молвят, падает на нем, будет тем огромным, чем больше сопротивление этого резистора. Зная ток и сопротивление дополнительного резистора, падение напряжения на нем просто подсчитать все по той же знакомой вам формуле U = IR, Тут U – падение напряжения, В; I – ток в цепи, A; R – сопротивление дополнительного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил излишек напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное примерно 2,5 В, свалилось на нити лампочки. Нужное сопротивление резистора можно отыскать по другой знакомой вам формуле R = U/I, где R – разыскиваемое сопротивление дополнительного резистора, Ом; U-напряжение, которое нужно погасить, В; I – ток в цепи, А. Для нашего примера сопротивление дополнительного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать либо наращивать напряжение, которое падает на дополнительном резисторе, и таким макаром регулировать ток в цепи. Но дополнительный резистор R в таковой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

Регулирование тока в цепи при помощи переменного резистора.

В данном случае при помощи движка резистора можно плавненько изменять напряжение, подводимое к нагрузке Н, а означает, плавненько регулировать ток, протекающий через эту нагрузку. Включенный таким макаром переменный резистор именуют реостатом, При помощи реостатов регулируют токи в цепях приемников, телевизоров и усилителей. В почти всех кинозалах реостаты использовали для плавного гашения света в зрительном зале. Есть, но, и другой метод подключения нагрузки к источнику тока с лишним напряжением – тоже при помощи переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Регулирование напряжения на нагрузке R2 при помощи переменного резистора включенного в электронную цепь потенциометром.

Тут R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания либо какой – то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое отчасти либо стопроцентно может быть подано к нагрузке R2. Когда движок резистора находится в последнем нижнем положении, к нагрузке напряжение вообщем не подается (если это лампочка, она пылать не будет). По мере перемещения движка резистора ввысь мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в последнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока огромное, нить лампочки перегорит). Можно опытным методом отыскать такое положение движка переменного резистора, при котором к нагрузке будет подано нужное ей напряжение. Переменные резисторы, включаемые потенциометрами, обширно употребляют для регулирования громкости в приемниках и усилителях. Резистор может быть конкретно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет 2-мя параллельными способами: через дополнительный резистор и основную нагрузку. Больший ток будет в ветки с минимальным сопротивлением. Сумма же токов обеих веток будет равна току, используемому на питание наружной цепи. К параллельному соединению прибегают в тех cлучаях, когда нужно ограничить ток не во всей цепи, как при поочередном включении дополнительного резистора, а лишь на каком – то участке. Дополнительные резисторы подключают, к примеру, параллельно миллиамперметрам, чтоб ими можно было определять огромные токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

elektrica.info

Закон ома

Соотношение между значениями тока, ЭДС и сопротивления в электрической цепи носит название закона Ома. В девятнадцатом веке Георг Ом вывел математические соотношения между основными характеристиками электрической цепи. Закон Ома говорит: чем больше напряжение, тем больше ток, и чем больше сопротивление, тем меньше ток. Математически этот закон представляется так: ток в цепи прямо пропорционален ЭДС и обратно пропорционален сопротивлению цепи.

В любой из грех приведенных формул при двух известных параметрах электрической цепи оставшийся неизвестным параметр может быть рассчитан. Закон Ома неприменим к цепям переменного тока, поскольку витки проводов вызывают различные эффекты при таком токе. Переменный ток будет обсуждаться в последующих главах. Тем не менее общие понятия закона Ома справедливы для цепей переменного тока.

Закон Ома делает возможным расчет значения недостающего множителя, если значения двух других известны или могут быть измерены. На 1.10 представлен простой способ запоминания закона Ома. Если в круге заштрихован один из множителей, остальные буквенные обозначения в круге дадут правильную формулу для расчета заштрихованного множителя.

Условные обозначения в этих формулах те же, что и в выражениях для закона Ома; при этом Р символизирует мощность в ваттах. Следующие три примера иллюстрируют расчет мощности для трех электрических цепей.

Все вокруг нас — твердые тела, жидкости и газы — состоит из материи. Материя может быть разбита на молекулы (мельчайшие частицы физических объектов) и атомы (мельчайшие частицы элемента, которые могут встречаться отдельно или в сочетании с другими атомами). Атом состоит из ядра (центральной части) и электронов (отрицательно заряженных), которые вращаются вокруг ядра наподобие планет, вращающихся вокруг солнца. Ядро состоит из протонов (положительно заряженных) и нейтронов (не имеющих заряда). Количество протонов, как правило, равно количеству электронов, что делает атом электрически нейтральным. При потере электрона атом становится положительно заряженным, а при захвате — отрицательно заряженным. Закон электрических зарядов утверждает, что одноименные заряды отталкиваются, а разноименные — притягиваются. Можно получить материалы с положительным или отрицательным зарядами.

Электроны могут приводиться в движение с помощью трения, химических реакций и магнетизма. Проводник — это материал, способный пропускать электроны и электричество. Большинство металлов являются проводниками. Изолятор — материал, который противодействует движению электронов или предотвращает его.

Существуют четыре важных параметра в любой электрической цепи: электродвижущая сила, ток, сопротивление и мощность. Электродвижущая сила цепи — это фактически действующее электрическое давление в ней, наподобие водяного давления в гидравлических системах. Электродвижущая сила электрической цепи измеряется в вольтах. Напряжение давления должно быть достаточным для преодоления сопротивления цепи. Переменный ток в промышленности используется исключительно для питания оборудования электроэнергией.

Количество электронов, протекающих в электрической цепи, называется электрическим током. Ток в электрической цепи измеряется в амперах. Ампер — это количество тока, которое проходит через сопротивление один Ом при напряжении один вольт.

Сопротивление электрической цепи измеряется в омах. Любая электрическая нагрузка имеет какое-нибудь сопротивление. Мощность — скорость потребления энергии электрической цепью. Мощность измеряется в ваттах и киловаттах. Поставщики электроэнергии в большинстве случаев пользуются киловатт-часами для расчетов с потребителями электричества. Киловатт-час — это мера электрической энергии, учитывающая продолжительность потребления энергии и ее мощность. Одна тысяча ватт, использованная за период времени один час, равнозначна одному киловатт-часу. Вольты, амперы, омы и ватты часто используются совместно с приставками кило- или милли-, чтобы представить большие или меньшие количества этих величин и избежать использования чрезвычайно больших или малых чисел.

Закон Ома дает соотношение между значениями тока, электродвижущей силы и сопротивлением электрической цепи. Это соотношение представляется в математической форме. Когда любые два параметра электрической цепи известны или могут измеряться, можно воспользоваться формулой закона Ома для нахождения третьего параметра. Мощность может рассчитываться с помощью выражения Р = 1-Е.

blockstroi.ru

Закон Ома

Всем привет, дамы и господа! Сегодня наконец речь пойдет о законе Ома. Да-да, это то, без знания чего вас заклюют на любом радиолюбительском форуме или паблике сотни уважаемых господ, которые в теме, пусть и не всегда действительно глубоко. Да что там паблики! Если ты, мой юный друг, посещаешь школу, лицей, гимназию или другое, без сомнения превосходное, учебное заведение, неправильный ответ на этот вопрос может привести в ярость почтенного преподавателя физики и закончиться для тебя не самым лучшим образом.

Сегодняшний урок статья (мы же не в школе, в самом деле) направлена на предотвращения такого нехорошего сценария развития событий путем приобщения к еще одной очень важной (на самом деле так) тайне радиоэлектроники.

Закон Ома на самом деле весьма прост. На великом и ужасном языке математики он выглядит следующим образом:

В этой формуле I – уже известный нами ток, U – напряжение, R – cопротивление. Как вы видите, все величины мы рассмотрели ранее, они нам уже известны. В этой же статье мы рассмотрим, как они связаны между собой. Более того, мы уже видели раньше эту формулу в статье про сопротивлениe, правда тогда мы договорились, что не будем пока забегать вперед.

Видите, зависимость совсем проста. Дифференциалов и страшных интегралов тут нет, а делить, вроде как вы, надуюсь, умеете. Так что на самом деле все несложно. Сила тока I в проводнике c сопротивлением R, оказывается, прямо пропорциональна приложенному к проводнику напряжению U и обратно пропорциональна сопротивлению проводника.

Резонный вопрос – а откуда, собственно, эта связь взялась и сфига я должен ей верить? Если вы его задали – поздравляю, господа, вы на правильном пути. Действительно, с какой это стати верить всему написанному на слово?

Та или иная зависимость может родиться двумя способами: результаты эксперимента или математический вывод формулок. Ну, здесь настолько простая формулка, что ответ один – эта зависимость получена экспериментальным путем уважаемым господином Георгом Омом. Грубо говоря, он взял источник напряжения (были в те времена так называемые «вольтовые столбы», кому интересно - гуглите) и куски металлической проволоки. Изменяя число вольтовых столбов (т.е. изменяя напряжение источника) или количество отрезков проволоки (т.е. изменяя сопротивление нагрузки), Ом получил данную зависимость. В тонкости физики измерений тех лет мы вникать не будем, это тема отдельной статьи. Кому интересно – гугл в помощь. Кто по-прежнему не верит – эксперимент в помощь. Вы всегда можете взять источник питания, который выдает точно известное напряжение, можете купить в магазине резистор с точно известным сопротивлением и мультиметром в режиме амперметра измерить протекающий в цепи ток. Дальше остается результат этого измерения сравнить с расчетным значением тока в цепи по приведенной формуле. Если вы все сделали правильно, результат эксперимента должен совпасть с расчетным значением. Схемка, иллюстрирующая этот эксперимент, приведена на рисунке 1.

Рисунок 1 – Иллюстрация закона Ома

Математика – математикой, а настоящего инженера должна интересовать в первую очередь физика процесса. К сожалению, есть люди даже среди почтеннейшей касты преподавателей, которые не уделяют должного внимания физике происходящего процесса, ограничиваясь лишь написанием формул, часто вообще без понимания сути происходящего. Если вы относите себя к их числу и вас устраивает данное положение дел, вероятно, есть смысл сейчас же безотлагательно покинуть данный ресурс. Невыполнение данного требования может повлечь существенные изменения в вашей психике! Автор не несет за это никакой ответственности!

Итак, физика процесса. Возьмем источник напряжения. Разумеется, не ортодоксальные вольтовые столбы, а, например, лабораторный источник питания. Возьмем нагрузку. Например, обычный резистор 1,2 кОм. Выставим на источнике питания напряжение 12 В. Внимание, вопрос, господа знатоки. Какой будет протекать ток через резистор? Используя написанную нами выше формулку, получаем величину тока

Т. е. ток через резистор равен 0,1 А или 100 мА.

Допустим, мы хотим увеличить протекающий ток. Как это можно сделать? Очевидно, двумя способами – поднять напряжение источника питания или уменьшить сопротивление нагрузки-резистора.

А если уменьшить протекающий ток? Аналогично – уменьшаем напряжение. Или увеличиваем сопротивление.

Важно понимать, господа, что напряжение и сопротивление – это первичные величины. Они задаются конкретными девайсами – источником питания и резистором-нагрузкой. Они... как там это говорят... самобытны и самодостаточны. Они существуют сами по себе и, собственно, отлично живут без какого-то там тока.

Сопротивление резистора ни в коем случае не зависит от источника напряжения! Оно ни в коем случае не зависит от протекающего тока! Оно может зависеть от материала резистора, от температуры, от формы, еще от чего-нибудь, но никак не от напряжения и тока (слышу вой уважаемый зануд, что это не так для нелинейных элементов – тссс! Спокойно, господа, до них тоже доберемся). От чего именно оно зависит, мы уже рассматривали здесь.

Напряжение источника питания тоже тут величина первичная. Она определяется и формируется источником питания. А именно – переизбытком электронов на одном из электродов.

Ток же здесь – вторичная величина, т.е. расчетная. Он существо подневольное, можно сказать, раб системы. Он зависит от напряжения и сопротивления. Сдохнет источник питания – каюк и току, он пропадет. Прикажет долго жить резистор, устав постоянно сопротивляться – на токе, несомненно, это тоже отразится (уменьшится или увеличится – отдельный вопрос, который решать будет все тот же уже почерневший резистор). Это рабство просто отлично характеризует картинка, которую мы любезно позаимствуем с pikaby .

Даже по выражению лиц на картинке отлично видно, кто тут подневольное существо, а кто командует парадом .

Читатель может возразить: "А как же источники тока?" Да, действительно есть такое понятие как "источник тока". Дескать, это такой девайс, у которого не напряжение первичная величина, а ток. То есть в теории он выдает через любое сопротивление строго один и тот же ток. Однако на практике возможности этих источников тока весьма ограничены. Как правило, они могут работать лишь при очень небольших нагрузочных сопротивлениях. Более того, если углубиться в физику процессов этих источников, то окажется, что там тоже идет игра за счет изменения напряжения. Поэтому-таки будем полагать, что первичной величиной является именно напряжение, а не ток. А про источники тока и источники напряжения потом поговорим более подробно.

В инженерной практике, равно как и в школьных задачах, возникает задача следующего рода. Мы намерили ток, например, величиной в 1 А через известный резистор с сопротивлением, скажем, 10 Ом. Вопрос задачи: определите напряжение источника питания.

Решается подобная задача весьма просто на основе того же закона Ома. Просто выражаем из уже написанной формулы напряжение:

Абсолютно аналогичным образом можно посчитать и сопротивление, если мы знаем напряжение и ток.

Итак, у нас теперь есть отличный инструмент, который связывает между собой напряжение, ток и сопротивление. Зная две из этих величины мы всегда сможем найти третью. Поверьте, на практике это встречается сплошь и рядом и это реально надо очень хорошо запомнить и понимать.

Ну что ж, господа, на этом, думаю, сегодня можно закругляться. Поскольку тема и правда очень важная, не буду вас сегодня грузить чем-то еще, лучше хорошо разобраться в этой. Всем огромной удачи и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

myelectronix.ru

Закон Ома - это... Что такое Закон Ома?

V — напряжение,I — сила тока,R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

— удельное сопротивление материала, из которого сделан проводник,
— его длина
— площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

U = U0eiωt — напряжение или разность потенциалов,
I — сила тока,
Z = Re−iδ — комплексное сопротивление (импеданс),
R = (Ra2 + Rr2)1/2 — полное сопротивление,
Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
Rа — активное (омическое) сопротивление, не зависящее от частоты,
δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

dal.academic.ru

Электрический ток. Закон Ома | ЭТО ФИЗИКА

Если изолированный проводник поместить в электрическое поле $\overrightarrow{E} $, то на свободные заряды $q$ в проводнике будет действовать сила $ \overrightarrow{F} = q\overrightarrow{E}$ В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю.

Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда.

Направленное движение заряженных частиц называется электрическим током.

За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока $I$ – скалярная физическая величина, равная отношению заряда $\Delta q$, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени $\Delta t$, к этому интервалу времени:

$$I = \frac{\Delta q}{\Delta t} $$

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.

Рисунок 1.8.1.

Упорядоченное движение электронов в металлическом проводнике и ток $I$. $S$ – площадь поперечного сечения проводника, $\overrightarrow{E}$ – электрическое поле

В Международной системе единиц СИ сила тока измеряется в Амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током.

Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы $A_{ст}$ сторонних сил при перемещении заряда $q$ от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

$$ЭДС=\varepsilon=\frac{A_{ст}}{q}. $$

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в Вольтах (В).

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов $\Delta \phi_{12} = \phi_{1} - \phi_{2}$ между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе $\mathcal{E}$, действующей на данном участке. Поэтому полная работа равна

$$U_{12} = \phi_{1} - \phi_{2} + \mathcal{E}$$

Величину U12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:

$$U_{12} = \phi_{1} - \phi_{2}$$

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока $I$, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению $U$ на концах проводника:

$$I = \frac{1}{R} U; \: U = IR$$

где $R$ = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит Ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока $I$ от напряжения $U$ (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:

$$IR = U_{12} = \phi_{1} - \phi_{2} + \mathcal{E} = \Delta \phi_{12} + \mathcal{E}$$$$\color{blue}{I = \frac{U}{R}}$$

Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.

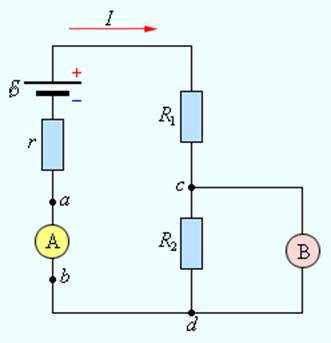
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.

Рисунок 1.8.2.

Цепь постоянного тока

По закону Ома

$$IR = \Delta\phi_{cd}$$

Участок (ab) содержит источник тока с ЭДС, равной $\mathcal{E}$.

По закону Ома для неоднородного участка,

$$Ir = \Delta \phi_{ab} + \mathcal{E}$$

Сложив оба равенства, получим:

$$I(R+r) = \Delta\phi_{cd} + \Delta \phi_{ab} + \mathcal{E}$$

Но $\Delta\phi_{cd} = \Delta \phi_{ba} = -\Delta \phi_{ab}$.

Поэтому :

$$\color{blue}{I=\frac{\mathcal{E}}{R + r}}$$

Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи (внутреннего сопротивления источника).

Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника ($R\ \ll r$), тогда в цепи потечет ток короткого замыкания

$$I_{кз}=\frac{\mathcal{E}}{r}$$

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой $\mathcal{E}$ и внутренним сопротивлением $r$. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.

Если внешняя цепь разомкнута, то $\Delta \phi_{ba} = -\Delta \phi_{ab} = \mathcal{E}$, т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.

Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной

$$\Delta \phi_{ba} = \mathcal{E} - Ir$$

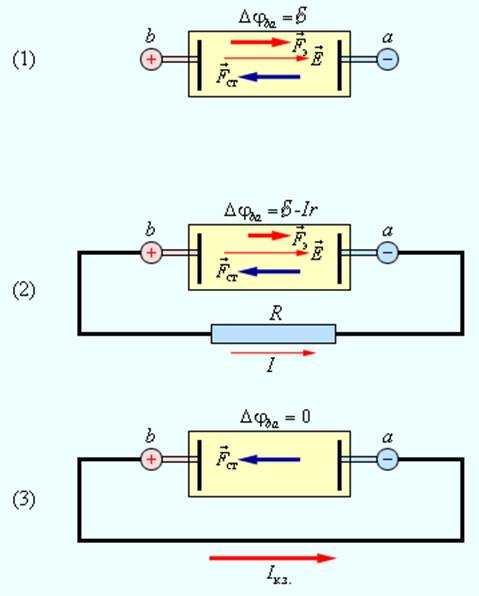
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной $\mathcal{E}$ и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность $\overrightarrow{E}$ электрического поля внутри батареи и силы, действующие на положительные заряды:$\overrightarrow{F}_{э}$ – электрическая сила и $\overrightarrow{F}_{ст}$ – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.

Рисунок 1.8.3.

Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением $R_{В}$. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:

$$R_{В} \gg R_{1}$$

Это условие означает, что ток $I_{В} = \Delta \phi_{cd} / R_{В}$, протекающий через вольтметр, много меньше тока $I = \Delta \phi_{cd} / R_{1}$, который протекает по тестируемому участку цепи.

Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением $R_{А}$. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию

$$R_{А} \ll (r + R_{1} + R{2})$$

чтобы при включении амперметра ток в цепи не изменялся.

Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.

Рисунок 1.8.4.

Включение амперметра (А) и вольтметра (В) в электрическую цепь