Примеры решения задач на законы Кирхгофа. Закон кирхгофа для электрической цепи решение задач

Примеры решения задач на законы Кирхгофа

Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.

Задача 1

Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

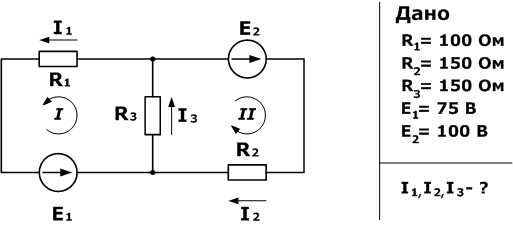
Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.

Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.

На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.

Уравнения для первого и второго контуров по второму закону будут:

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.

Задача 2

Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

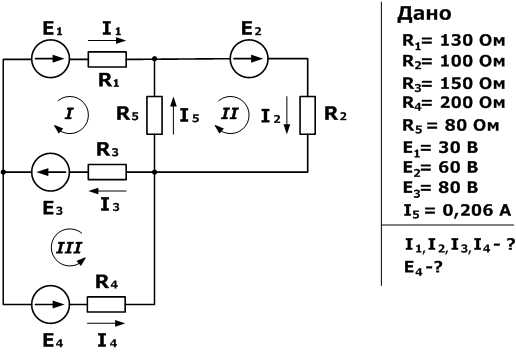
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2

Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.

На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины

Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.

Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.

Читайте также - расчет простых цепей постоянного тока

electroandi.ru

Алгоритм решения задач на законы Кирхгофа

Задачи на применение закона Кирхгофа решаются в школе не часто, и не во всех классах. Работая в школе, я давала законы Кирхгофа только тем ребятам, кто готовился к олимпиадам по физике, и учащимся, которые готовились в ВУЗы.

Задачи на использование законов Кирхгофа есть даже не всех сборниках задач, рекомендованных для использования в средней школе.

Ниже приведён алгоритм решения задач по данной теме. Алгоритм не сложен. Использование данного алгоритма поможет Вам в решении задач по этой теме.

Итак, начнем. Сначала необходимо выполнить некоторые подготовительные операции.

перерисовать схему
указать направление ЭДС источников тока
указать предполагаемое направление токов, текущих в каждом резисторе (если итоговый ответ будет отрицательным, то направление тока было изначально выбрано не верно)
выбрать направление обхода для всех линейно независимых контуров

После проведения предварительных операций, приступаем собственно к решению самой задачи.

Записываем первый закон Кирхгофа: сумма токов, втекающих и вытекающих в данный узел, равна нулю.

Важно! Если ток втекает в узел, то он берётся со знаком «плюс», если вытекает, то со знаком «минус». Число уравнений второго закона Кирхгофа равно n-1, где n — число узлов в данной схеме. (Узел — точка, в которой соединяются три проводника и более).

Записываем второй закон Кирхгофа для всех линейно независимых контуров: Сумма ЭДС в контуре равно сумме падений напряжений в каждом из этих контуров.

Важно! Если направление ЭДС совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «плюс». Если направление ЭДС не совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «минус». Если направление тока совпадает с направлением обхода контура, то падение напряжения на данном участке берётся со знаком «плюс». Если направление тока через какой-либо резистор не совпадает с направлением обхода в данном контуре, то падение напряжения берётся со знаком «минус».

Решаем систему получившихся уравнений, относительно неизвестных величин.

Чаще всего в задачах этого типа, основную сложность представляет именно решение системы получившихся уравнений.

Ниже показан пример решения задачи с использованием законов Кирхгофа. Обратите внимание ещё раз на основные этапы решения. Они полностью соответствуют алгоритму, описанному выше.

Вот условие этой задачи.

Электрическая цепь состоит из двух гальванических элементов, трех резисторов и амперметра. В этой цепи R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, ЭДС элемента ?1 = 2 В. Амперметр регистрирует ток I3 = 50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС ?2 второго элемента. Сопротивлением амперметра и внутренним сопротивлением источников пренебречь.

Удачи в освоении этой довольно сложной темы!

Возникающие вопросы можете оставлять в комментариях.

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.

Написать комментарий

fizika-doma.ru

2.2. Законы Кирхгофа

Согласно первого закона Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю

∑I = 0.

Поскольку речь идет об алгебраической сумме ∑I, необходимо учитывать знаки слагаемых токов. Входящие в узел токи принято считать положительными, выходящие – отрицательными. Для узла "а" (рис. 2.5) имеем

I1 + I2 - I3 = 0.

Согласно второго закона Кирхгофа алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах контура

∑E = ∑R·I.

Для составления уравнения по второму закону Кирхгофа произвольно выбирают направление обхода контура. Принято ЭДС, токи и напряжения считать положительными, если они совпадают по направлению с направлением обхода контура, а если не совпадают – отрицательными. При обходе контура E1, E2, R2, R1 электрической цепи (рис. 2.5) по часовой стрелке имеем

E1 - E2 = R1·I1 - R2I2.

2.3. Преобразования в электрических цепях

При расчётах сложных электрических цепей применяют формулы последовательного (смотреть пункт 2.1), параллельного, смешанного соединения элементов, а также преобразования "треугольника" в "звезду" и обратно. Рассмотрим эти соотношения.

2.3.1. Параллельное соединение (рис. 2.6)

Рис. 2.6. – Параллельное соединение элементов

При таком соединении элементов общее сопротивление определяется выражением

При двух сопротивлениях, соединенных параллельно

Если R1 = R2 = … Rn, то

где п – число параллельно соединенных элементов.

2.3.2. Смешанное соединение (рис. 2.7)

Смешанным соединением называют сочетание последовательного и параллельного соединений резисторов.

При смешанном соединении элементов для эквивалентного преобразования пользуются методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.

Поясним это на конкретном примере расчета электрической цепи (рис.1.3).

Рис.1.3. Смешанное соединение элементов.

Рис. 2.7. – Смешанное соединение элементов

2.3.3. Преобразование "треугольника" в "звезду" (рис. 2.8)

2.2.4. Преобразование "звезды" в "треугольник" (рис. 2.8)

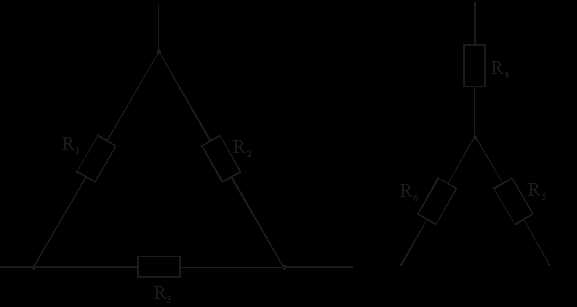Рис. 2.8. – Соединение сопротивлений в "треугольник" и "звезду"

2.4. Расчет разветвленной электрической цепи с одним источником энергии

При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС, сопротивления элементов электрической цепи. Задача расчета электрической цепи сводится к определению токов в ветвях. По найденным токам можно рассчитать напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников, сечения проводников.

Для расчета электрических цепей с одним источником энергии применяется метод эквивалентных преобразований, заключающийся в постепенном преобразовании и замене последовательно и параллельно соединенных элементов эквивалентными. Всю группу элементов цепи заменяют одним эквивалентным. Преобразования начинают в ветвях, наиболее удалённых от источника. Затем в преобразованной (предельно простой) цепи по закону Ома определяют ток. Полученные в процессе преобразования расчетные схемы позволяют определить токи во всех остальных ветвях.

Пример 1: Рассчитать эквивалентное сопротивление цепи Rэкв и, токи в каждом резисторе.

Дано: R1 = 3 Ом; R2 = 2 Ом; R3 = 5 Ом; R4 = 10 Ом; E = 50 В.

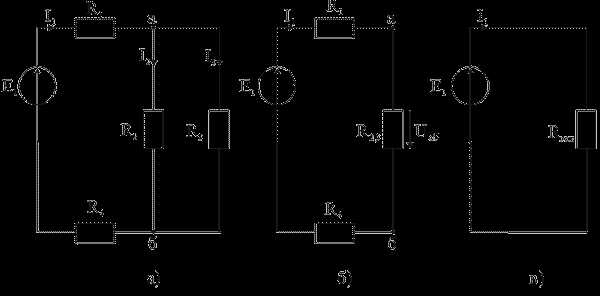Рис. 2.9 - Пример эквивалентных преобразований: а) схема электрической цепи до преобразования; б) расчетная схема после первого преобразования; в) - расчетная схема после второго (окончательного) преобразования

Определить токи в ветвях схемы, представленной на рис. 2.9, а.

Выбираем направления токов в ветвях. Преобразуем параллельно соединенные резисторы R2 и R3, заменяя их эквивалентным элементом R2, 3

Расчетная схема после первого преобразования показана на рис. 2.9, б.

Проводим второе преобразование. Для этого последовательно соединенные резисторы R1, R2, 3, R4 заменяем одним эквивалентным RЭКВ.

RЭКВ = R1 + R2, 3 + R4 = 3 + 1,43 + 10 = 14,43 Ом.

Теперь исходная схема сведена к простейшей, показанной на рис. 2.9, в, в которой

Для определения токов I2 и I3, необходимо определить напряжение Uаб, рис. 2.9, а, которое рассчитываем по рис. 2.9, б

Uаб = R2, 3·I1 = 1,43·3,47 = 4,96 В.

Возвращаясь к схеме рис 2.9, а, получим

Для проверки правильности расчета токов составляем баланс мощности. Мощность, вырабатываемая всеми источниками энергии в цепи, должна быть равна мощности, потребляемой всеми приёмниками электрической энергии (нагрузкой). Относительная погрешность расчета не должна превышать одного процента.

Мощность, вырабатываемая источником ЭДС

РИ = Е·I1 = 50·3,47 = 173,5 Вт.

Мощность, потребляемая нагрузкой

Погрешность баланса мощности

Если баланс сходится с допустимой погрешностью, то расчет токов выполнен верно.

Пример выполнения задачи 1.

Для электрической цепи постоянного тока, приведенной на рис. 4:

1. Рассчитать эквивалентное сопротивление цепи.

2. Рассчитать ток в каждом резисторе.

3. Проверить выполнение первого закона Кирхгофа во всех узлах схемы и второго Закона Киhхгофа для одного из контуров.

4. Определить мощности, рассеиваемые на резисторах схемы.

5. Проверить выполнение баланса мощностей

Рис. 4. Электрическая цепь постоянного тока

1. Расчет эквивалентного сопротивления цепи проводим методом последовательных эквивалентных преобразований..

а) б) в)

Рис. 5. "Этапы эквивалентного преодразования электрической цепи

Эквивалентное сопротивление ветвей R3 и R4 соединенных параллельно определяем по формуле:

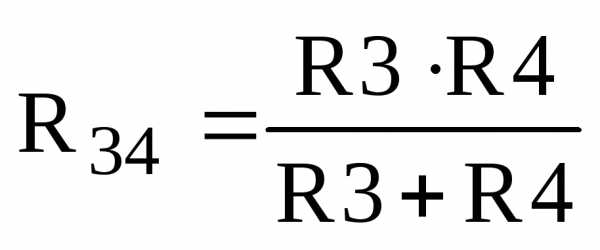Эквивалентное сопротивление элементов R2, R34 и R5, соединенных последовательно находим по формуле:

Эквивалентное сопротивление всей цепи (R2345 и R1 -соединены параллельно):

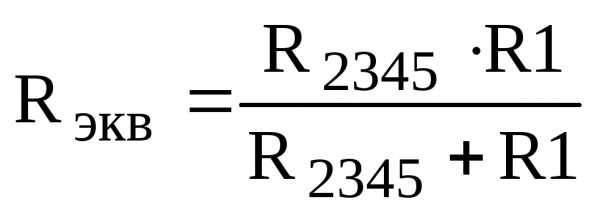
2. Рассчитаем токи во всех ветвях.

Ток, потребляемый цепью от источника питания:

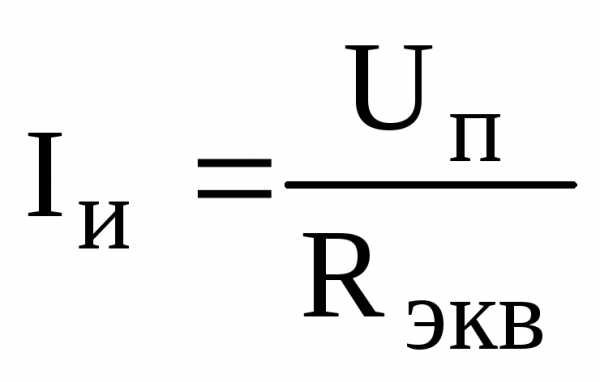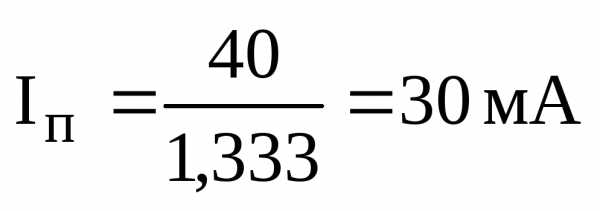Ток в ветви R1:

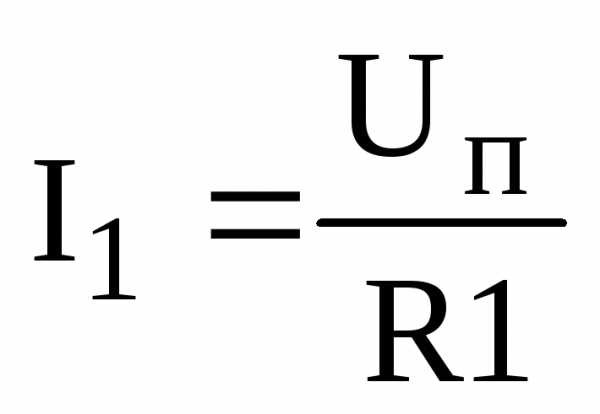
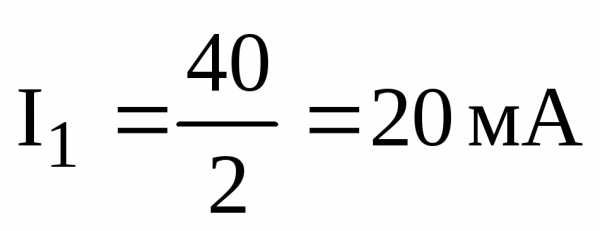
Ток в ветви R2345:

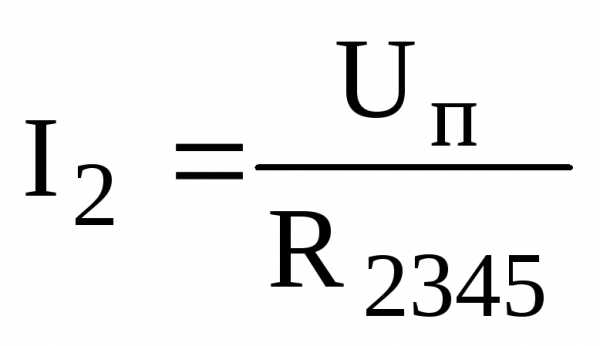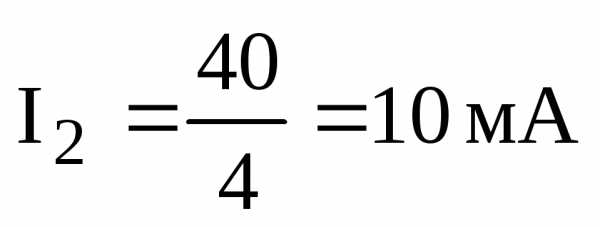Определяем потенциал узла «б»:

Определяем потенциал узла «в»:

Очевидно, что I5 = I2, откуда

Определяем разность потенциалов между узлами «б» и «в»:

Определяем токи в ветвях R3 и R4:

;

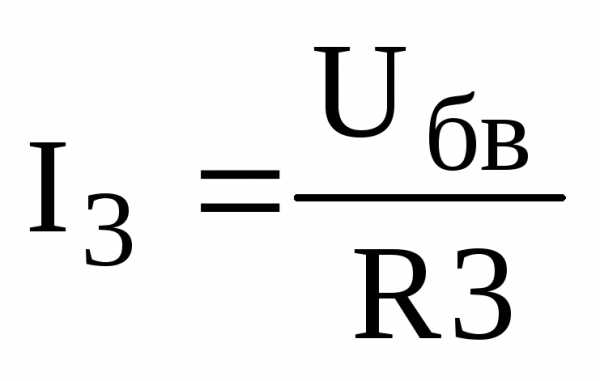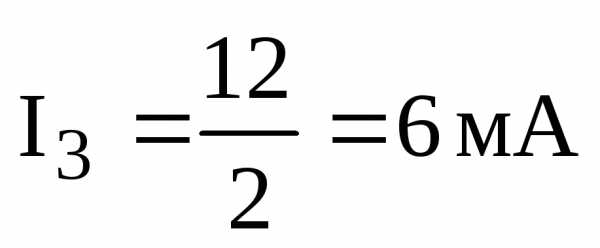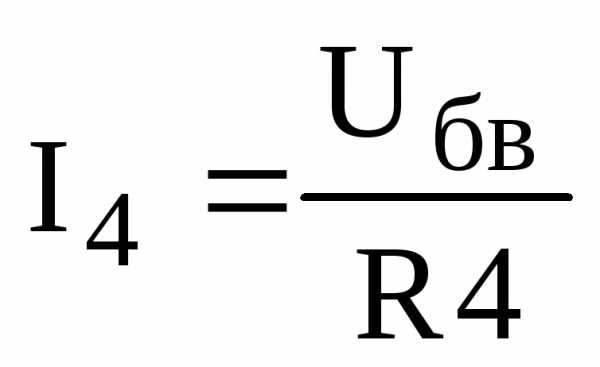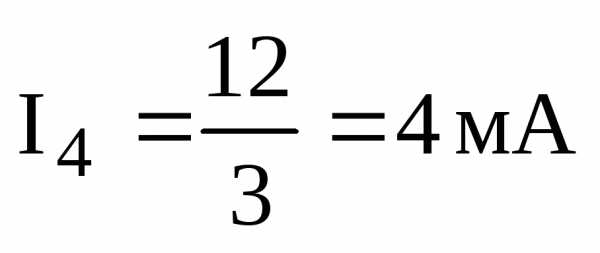3. Проверяем выполнение первого закона Кирхгофа для токов в узлах.

Для узла «а»: ,

Для узла «б»: ,

Для узла «в»: ,

Проверяем выполнение второго закона Кирхгофа для контура R5, R3, R2, R1:

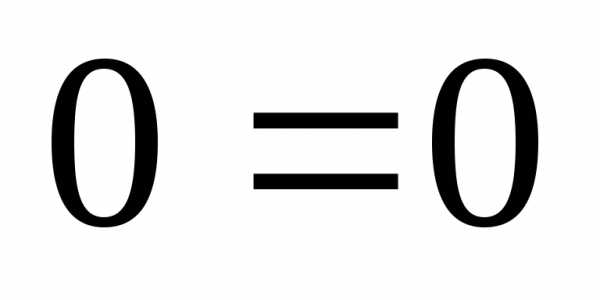4. Определяем мощности, рассеиваемые на резисторах:

;

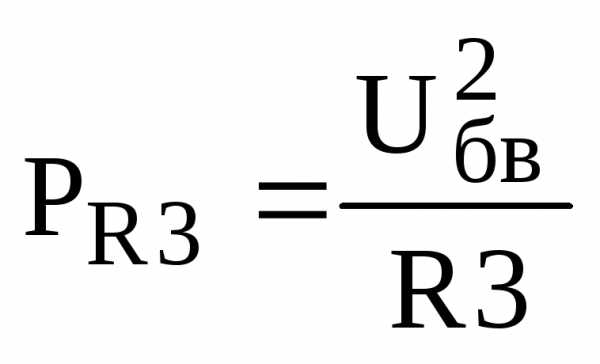5. Проверяем выполнение баланса мощностей.

Мощность, потребляемая цепью от источника питания:

Составляем уравнение для проверки баланса мощностей:

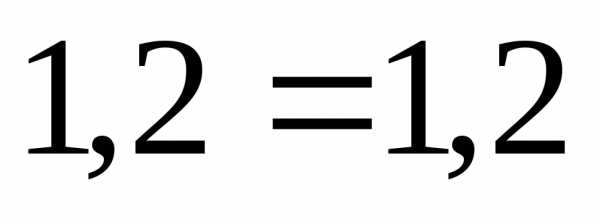Баланс мощностей выполняется.

Методические указания к выполнению задания 2.

Методы расчета цепей постоянного (переменного) тока

Под расчетом цепи, в общем случае, понимают нахождение токов во всех ветвях схемы.

Основные методы расчета:

1. Метод токов ветвей.

2.Метод контурных токов.

3. Метод узловых напряжений.

4. Метод наложения.

5. Метод эквивалентных преобразований

Метод токов ветвей

В общем случае токи сложной электрической цепи могут быть определены в результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа. Для однозначного нахождения всех токов необходимо составить в уравнений, где в- число ветвей схемы (без источников тока).
Последовательность расчета следующая:

1. Проводят топологический анализ схемы.

1.1. обозначают токи во всех ветвях (I1, I2, …,Iв), произвольно выбирают их положительное направление и обозначают на схеме стрелками;

1.2. подсчитывают общее число узлов у и определяют число независимых узлов Nу=у-1 и показывают их на схеме;

1.3. подсчитывают число независимых контуров Nk = в-у+1, и показывают их на схеме дугой.

2. По первому закону Кирхгофа для независимых узлов и по второму закону Кирхгофа для независимых контуров относительно токов ветвей записывают уравнения. После приведения подобных членов они сводятся к системе линейных алгебраических уравнений (ЛАУ)

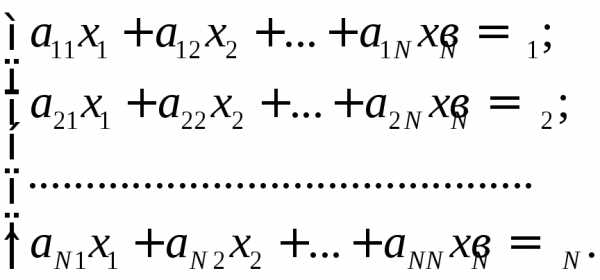
где xi =Ii– искомые токи ветвей; aji – постоянные коэффициенты, зависящие от параметров пассивных элементов схемы; вi – постоянные величины, зависящие от параметров активных элементов схемы.

3. Решая систему из в уравнений относительно токов, по методу Крамера находят токи во всех ветвях схемы:

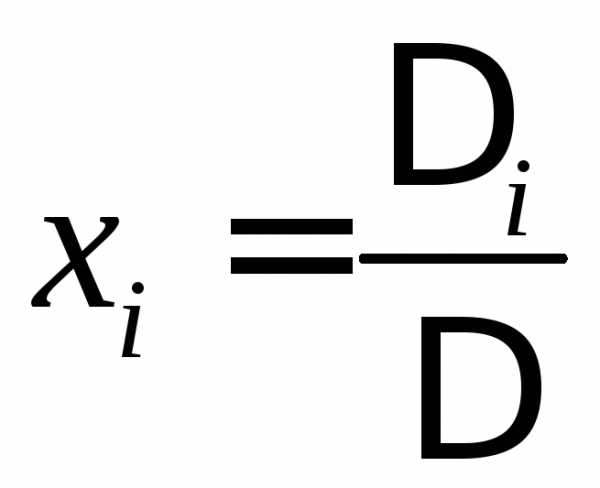
где D – главный определитель системы; Di – определитель, получается из главного D путем замены i-го столбца на столбец свободных членов вi.

Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным направлениям. I1

Пример 1. Для электрической цепи рис. 1.1 n = 2, m = 3, и расчет токов цепи осуществляется путем решения следующей системы уравнений

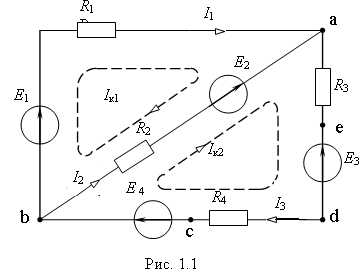
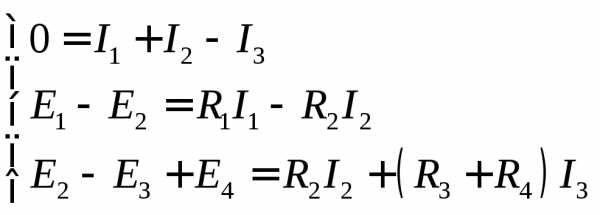
studfiles.net

Правила Кирхгофа, теория и примеры задач

Очень часто электрическая цепь включает несколько источников тока и сопротивлений, которые соединены разными способами. Такую цепь называют сложной разветвленной электрической цепью. Значимыми для составления систем уравнений, позволяющих провести расчеты в сети постоянного тока, являются ее узлы и замкнутые контуры. Расчеты любой сети можно проводить, используя закон Ома и закон сохранения заряда. Но использование специальных правил, которые называют правилами Кирхгофа (иногда законами Кирхгофа) позволяют упростить процедуру составления уравнений для вычислений. Всего выделяют два правила Кирхгофа.

Первое правило Кирхгофа

Довольно часто в электрической цепи в одной точке сходятся более двух проводников, по которым текут токи. Такие точки в цепи называют узлами или разветвлениями. В любом узле, если ток в цепи постоянен, полное изменение заряда за некоторый промежуток времени равно:

где суммирование проводят с учетом знаков силы тока. Если мы имеем дело с постоянным током в цепи, то потенциалы всех ее точек остаются неизменными. Значит, в узлах не может накапливаться заряд. Поэтому рассматривая силу тока, как алгебраическую величину запишем:

где N – число токов, которые сходятся в узле. Выражение (2) носит название первого правила Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.

Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.

Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.

Второе правило Кирхгофа

Во втором правиле Кирхгофа рассматривают замкнутые контуры, поэтому оно называется правилом контуров. Формулируется это правило Кирхгофа следующим образом: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

Величины называют падениями напряжения. Прежде, чем применять второй закон Кирхгофа определяются с направлением положительного обхода контура. Выбирается направление произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго закона для данного контура входит с положительным знаком. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, сто ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа является следствием закона Ома.

Примеры решения задач

ru.solverbook.com

Законы Кирхгофа, теория и примеры задач

Законы Кирхгофа (или правила Кирхгофа) – это приемы, которые используют для того, чтобы упрощать процедуру составления систем уравнений необходимых при расчетах сложных разветвленных цепей постоянного тока. Разветвленными цепями называют цепи, которые содержат несколько замкнутых контуров с несколькими источниками ЭДС.

Узлом цепи называют такую точку цепи, в которой сошлись три или более проводников с токами.

Первый закон Кирхгофа

Первый закон Кирхгофа еще называют правилом узлов. Так как он касается именно узлов цепи и токов в них. Словесно этот закон формулируется следующим образом: Сумма токов в цепи с учетом их знаков равна нулю. В математическом виде этот закон представляют как формулу:

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.

Второй закон Кирхгофа

Во втором законе Кирхгофа рассматривают контуры, поэтому он еще называется правилом контуров. Формулируется второй закон Кирхгофа так: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

Величины еще называют падениями напряжения. Прежде, чем применять второй закон Кирхгофа определяются с направлением положительного обхода контура. Выбирается направление произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго закона для данного контура входит с положительным знаком. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника.

Второй закона Кирхгофа является следствием закона Ома.

Любую цепь можно рассчитать при помощи закона сохранения заряда и закона Ома, правила Кирхгофа являются лишь подходами, упрощающими расчетные задачи.

При составлении уравнение, используя законы Кирхгофа, следует внимательно следить за расстановкой знаков у токов и ЭДС.

Примеры решения задач

ru.solverbook.com

Расчет электрических цепей с применением законов Кирхгофа и Ома

Законы Кирхгофа наиболее общие. Они являются отдельным случаем универсальных уравнений электрического поля относительно произвольных электрических цепей с сосредоточенными параметрами. Закон Ома используется для расчета только линейных цепей.Алгоритм расчета: 1. Начертить по принципиальной схеме схему замещения; упростить схему, преобразовав последовательно и параллельно соединенные резисторы в эквивалентные, пронумеровать ЭДС соответствующих ветвей, узлы; произвольно выбрать и обозначить положительные направления токов в ветвях. 2. Записать n – 1 уравнений по первому и m – (n – 1) уравнений по второму закону Кирхгофа, где n – количество узлов, m – количество ветвей в цепи. Если бы мы записывали n уравнений по первому закону Кирхгофа, то одно из них – это линейная комбинация оставшихся, что привело бы к линейной зависимости уравнений.Источник тока J входит только в уравнение первого закона Кирхгофа (баланс тока в узлах) и переносится как известное в правую часть уравнения. Для схемы (рис. 1) n = 3, m = 4.Смотрите еще: Пример решения задачи по правилам Кирхгофа № 1 Пример решения задачи по правилам Кирхгофа № 2 Пример решения задачи по правилам Кирхгофа № 3 Рис. 1. Ветвь с идеальным источником тока не учитывается, поскольку ее сопротивление бесконечно велико. Уравнение по первому закону Кирхгофа при n – 1 = 2 для узла 1: – I1 – I3 + I4 + J = 0; для узла 2: I1 + I2 – I4 = 0. Уравнение по второму закону Кирхгофа при m – (n – 1) = 4 – 2 = 2 для контура 1 (направление обхода указано пунктиром): I1R1 + I2R2 = E1; для контура 2 (направление обхода то же самое, но можно было взять и противоположное): I2R2 – I3R3 – I4R4 = – E2. 3. Решить систему уравнений относительно тока I: Если среди компонент вектора I есть отрицательные, то это означает, что их направление противоположно положительному направлению, приведенному в схеме (рис. 1). 4. По закону Ома определить напряжения на элементах. Сложность использования этого метода связана с чрезмерно большой размерностью систем уравнений.

freewriters.narod.ru

Законы Кирхгофа для электрической цепи

Правильнее было бы говорить правила Кирхгофа для расчетов сложных электрических цепей постоянного тока. Электрическая цепь на практике может состоять из нескольких резисторов и источников тока. Такие цепи называют разветвленными. Уравнения позволяющие провести расчеты, например, сил токов, текущих в сопротивлениях, в любых сетях можно составить, воспользовавшись законом Ома и законом сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов и принципиально нового ни чего не привносят, однако, с их помощью можно упростить процедуру написания необходимых уравнений. Существует два правила Кирхгофа для электрических цепей постоянного тока. Одно правило называют правилом узлов, так как оно связывает в одно уравнение токи, сходящиеся в узле. Второе правило касается замкнутых контуров, которые можно выделить в сложной цепи.

Первый закон (правило) Кирхгофа

В электрической цепи в одной точке могут сходиться более двух проводников с токами, тогда такую точку цепи называют узлом (разветвлением). Учитывая, что сила тока алгебраическая величина для любого узла:

где N – число токов, которые сходятся в узле. Выражение (1) называют первым правилом Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.

Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.

Первое правило Кирхгофа является следствием закона сохранения заряда.

Второй закон (правило) Кирхгофа

Во втором правиле Кирхгофа рассматриваются замкнутые контуры, поэтому оно носит название правила контуров: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа является следствием закона Ома.

Примеры решения задач

ru.solverbook.com