Измерение ёмкостей методом вольтметра - амперметра. Способы измерения емкости

Измерение реактивного сопротивления индуктивности и емкости

В жизни радиолюбителя, инженера, монтажника, наладчика или студента иногда возникают ситуации когда нужно измерить не только активное сопротивление элемента, но и реактивное (индуктивность или емкость). Измерения эти проводят косвенным методом (вольтметр, ваттметр, амперметр) и чтобы получить более точные результаты применяют мостовой метод.

Косвенный метод (ваттметр, вольтметр, амперметр)

Этот метод наиболее прост по своей реализации, так как не требует специальных схем включения, а требует всего лишь трех приборов – амперметра, ваттметра и вольтметра. Измерив действующие значения напряжения U и тока I, мы можем получить полное сопротивление . Измерив активную мощность Р получим активное сопротивление элемента:

Соответственно реактивное будет равно:

Если искомое сопротивление индуктивное:

Емкостное:

Где ω – циклическая частота сети .

Схема установки ниже: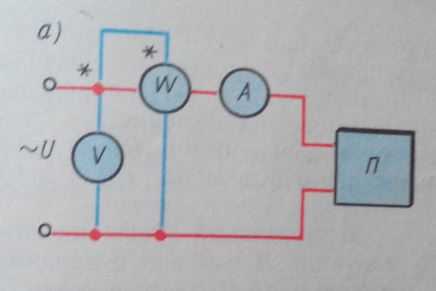

Этот метод проще мостового, но для его применения необходимо три измерительных прибора, что не всегда удобно.

Мостовой метод

Данная схема обычно применяется в лабораториях, где есть образцовые элементы. Схемы приведены ниже – для измерения индуктивности (R1 и L1):

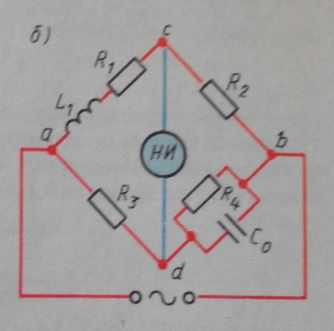
Плечи моста имеют сопротивления в комплексных числах:

Выразив это через общее уравнение моста мы получим:

Приравняв мнимые и вещественные составляющие мы сможем получить формулы для определения R1 и L1, а именно:

Ниже показана схема для измерения емкости:

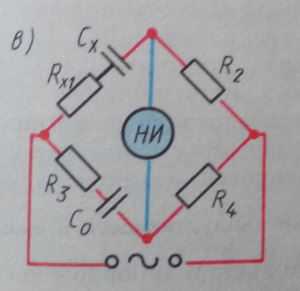
Проведя те же действия что и для индуктивности получим:

Современные методы измерения индуктивности и емкости

Методы указанные выше были актуальны ранее, когда электронные устройства еще не получили такого развития. На видео ниже показаны измерения индуктивности и емкости с помощью современных измерительных приборов. Но к сожалению такие устройства имеют довольно большую погрешность, поэтому для более точного измерения, как правило применяют мостовой метод.

elenergi.ru

Метод измерения Измерение емкости конденсатора можно осуществить различными методами

Работа добавлена на сайт samzan.ru: 2016-06-09

Напряжение на батарее равно сумме напряжений на каждом конденсаторе:

, (20)

где .

Преобразуем выражение (20) в соответствии с (9):

откуда получаем формулу для расчета емкости батареи конденсаторов

. (21)

При последовательном соединении конденсаторов величина, обратная емкости батареи, равна сумме величин, обратных емкостям конденсаторов, входящих в батарею.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Метод измерения

Измерение емкости конденсатора можно осуществить различными методами. В данной работе в основу измерения емкости положено соотношение между зарядом конденсатора q, его емкостью C и разностью потенциалов U на обкладках конденсатора (9):

. (22)

Измерение емкости конденсатора включает в себя градуировку интегратора тока и определение неизвестной емкости двумя методами.

В данной работе для измерения заряда используется интегратор тока. Такое название прибора обусловлено формулой, связывающей величину заряда конденсатора , прошедшего при его полном разряде через интегратор, с изменяющимся током разряда :

. (23)

При этом величина заряда, прошедшего через интегратор, пропорциональна показанию вольтметра на его выходе:

, (24)

где градуировочная постоянная интегратора.

Расчетную формулу для измеряемой емкости найдем, используя равенства (22) и (24):

. (25)

Определение градуировочной постоянной (градуировку интегратора) выполняют также с помощью формулы (25), проводя измерения для эталонного конденсатора с известной емкостью . При этом выражение

(26)

позволяет рассчитать величину (величины с индексом «э» относятся к измерениям с эталонным конденсатором).

Для проверки правильности градуировки интегратора нужно с его помощью провести измерение неизвестной емкости . Затем значение полученной емкости необходимо сравнить со значением , измеренным другим методом, например, с помощью мультиметра.

2. Описание экспериментальной установки

Схема электрической цепи представлена на рис. 8, монтажная схема

на рис. 9.

Рис. 8. Электрическая схема: 1 регулируемый источник постоянного напряжения «0…+15 В»; 2 переключатель; 3 миниблок «Ключ»;

4 исследуемый конденсатор С; 5 демпфирующий ключ; 6 интегратор тока; 7 миниблок «Интегратор тока»; 8, 9 мультиметры (режим V20 В, входы COM, VΩ)

Для зарядки конденсатора переключатель 2 устанавливают в положение «А», а демпфирующий ключ 5 замыкают (положение «Сброс»). Конденсатор заряжают до напряжения (не более 2 В), контролируемого вольтметром 9. Перед измерением демпфирующий ключ 5 размыкают, а переключатель 2 переводят в положение «В». При этом заряд, имеющийся на обкладках конденсатора, пройдет через интегратор тока и будет зафиксирован вольтметром 8 (показание вольтметра ). В дальнейшем вследствие утечек напряжение, зафиксированное вольтметром 8, может меняться.

Рис.9. Монтажная схема:

3 миниблок «Ключ»; 7 миниблок «Интегратор тока»; 8, 9 мультиметры

3. Выполнение измерений

1. Для правильного выбора величины напряжения зарядки, отчитываемому по мультиметру 9, в начале измерений возьмите наибольшую измеряемую емкость. Она получается при параллельном соединении конденсаторов и .

2. Соберите электрическую цепь по схеме, приведенной на рис. 9, подключив конденсаторы и параллельно. Значение эталонной емкости запишите в табл. 1.

3. Включите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров. Нажмите кнопку «Исходная установка».

4. Зарядите конденсаторы, для этого:

а) демпфирующий ключ 5 установите в положение «Сброс»;

б) переключатель 2 (тумблер) установите в положение «А»;

в) изменяя напряжение зарядки конденсатора кнопками установки напряжения «0…+15 В», установите его не более 2 В (отсчет по мультиметру 9).

5. Разрядите заряженные конденсаторы через интегратор, для этого:

а) разомкните демпфирующий ключ 5;

б) переведите переключатель 2 в положение «В». Если при этом загорится индикатор перегрузки у интегратора тока, уменьшите напряжение зарядки конденсаторов. Запомните максимальное показание мультиметра 8 непосредственно после разряда конденсатора.

6. Повторите пп. 4 и 5 несколько раз, подобрав такое напряжение зарядки (показания мультиметра 9) , при котором напряжение разрядки (показания мультиметра 8) составило бы 810 В (величина, пропорциональная заряду конденсатора). Запишите напряжение в табл. 1 и далее в ходе лабораторной работы не изменяйте его.

Таблица 1. Напряжения на конденсаторах и на батареях конденсаторов

№	Эталонный конденсатор = мкФ	Определение емкости
		Неизвестный конденсатор	Соединение конденсаторов
			параллельное	последовательное
	= В	= В	= В	= В
	,В	,В	,В	,В
1
2
3
4
5
Среднее

7. Не меняя напряжение зарядки , выполните 5 измерений , записывая значения в табл. 1.

8. Соедините и последовательно. Напряжение оставьте равным . Выполните 5 измерений и запишите результаты в табл. 1.

9. Проведите отдельно измерения величины для эталонного конденсатора и величины для конденсатора неизвестной емкости .

Величины и остаются равными и . Результаты измерений записываются в табл. 1.

10. Проверьте правильность градуировки интегратора, для этого:

а) с помощью мультиметра измерьте неизвестную емкость конденсатора ;

б) результат запишите в табл. 2 (погрешность измерения мультиметром =5 %).

11. Выключите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров.

4. Обработка результатов измерений

1. Используя данные табл. 1, рассчитайте градуировочную постоянную (26)

2. По формуле (25) рассчитайте: емкость неизвестного конденсатора

емкость параллельно соединенных конденсаторов

и емкость последовательно соединенных конденсаторов

Результаты расчетов запишите в табл. 2.

Таблица 2. Электроемкости неизвестного конденсатора и батарей конденсаторов

Неизвестная емкость , мкФ	Емкость соединения С , мкФ
	Параллельное	Последовательное
экспер.	имерен.	экспер.	расчетное	экспер.	расчетное

=	=	=

3. Используя значения емкостей и , по формулам для параллельного и последовательного соединений конденсаторов рассчитайте

и .

Результаты расчетов запишите в табл. 2.

4. Найдите относительное отклонение экспериментальных значений от расчетных в %:

;

Результаты расчетов запишите в табл. 2.

5. Найдите относительное отклонение от (результатов измерений неизвестной емкости двумя методами) в %: .

Результат расчета запишите в табл. 2.

6. По величинам этих отклонений сделайте заключение о точности измерений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

для самостоятельной подготовки

к выполнению лабораторной работы

Дайте определение электроемкости уединенного проводника.

Запишите формулу для емкости уединенного проводящего шара в диэлектрической среде.

От каких величин зависит электроемкость уединенного проводника?

Дайте определения конденсатора и его электроемкости.

Назовите три основных вида конденсаторов, используемых в технике. (Вид конденсатора определяется формой его обкладок.)

Запишите формулу для емкости плоского конденсатора.

От каких величин зависит электроемкость конденсатора?

В чем преимущества конденсатора перед проводником такой же формы и размеров при сравнении их электроемкостей?
Как изменится емкость конденсатора при изменении диэлектрической проницаемости среды и расстояния между его обкладками в случаях, когда:

а) конденсатор отключен от источника тока;

б) конденсатор подключен к источнику тока.

Запишите три соотношения (формулы) при параллельном соединении конденсаторов:

а) между напряжением на батарее конденсаторов и напряжениями на отдельных конденсаторах этой батареи;

б) между зарядом на батарее и зарядами на отдельных конденсаторах этой батареи;

в) между емкостью батареи и емкостями отдельных конденсаторов этой батареи.

Как надо соединить конденсаторы, чтобы получить наибольшую результирующую емкость?

Запишите три соотношения (формулы) при последовательном соединении конденсаторов:

а) между напряжением на батарее конденсаторов и напряжениями на отдельных конденсаторах этой батареи;

б) между зарядом на батарее и зарядами на отдельных конденсаторах этой батареи;

в) между емкостью батареи и емкостями отдельных конденсаторов этой батареи.

Как надо соединить конденсаторы, чтобы получить наименьшую результирующую емкость (меньшую, чем наименьшая емкость одного из соединяемых конденсаторов)?

Какую величину и каким образом измеряют интегратором тока в данной работе?

Как находят величину градуировочной постоянной?

Как измеряют величину неизвестной емкости конденсатора?

Савельев, И.В. Курс общей физики В 3 т. Т. 2 / И.В. Савельев. М.: Наука, 1988

Иродов, И.Е. Электромагнетизм. Основные законы В 5 т. Т. 3 / И.Е. Иродов. М. СПб: Физматлит, 2001.

Волков, В.Н. Физика В 3 т. Т. 2 / В.Н. Волков, Г.И. Рыбакова, М.Н. Шипко; Иван. гос. энерг. ун-т. Иваново, 1993.

Крылов, И.А. Физические основы электромагнитных процессов в технических средствах автоматизации: учеб. пособие /И.А. Крылов; Иван. гос. энерг. ун.-т.- Иваново, 2004.

PAGE 20

samzan.ru

Измерение ёмкостей методом вольтметра - амперметра — МегаЛекции

Метод вольтметра - амперметра применяют для измерения сравнительно больших ёмкостей. Питание измерительной схемы обычно производят от источника тока низкой частоты: F = 50...1000 Гц, поэтому оказывается возможным пренебречь активными потерями в конденсаторах, а также влиянием реактивных параметров измерительных приборов и паразитными связями.

Рис.1. Схемы измерения ёмкостей методом вольтметра-амперметра

ёСхема измерений представлена в двух вариантах на рис. 1. Проверяемый конденсатор Сх включается в цепь переменного тока известной частоты F, и реостатом (или потенциометром) R устанавливают требуемое по условиям испытания либо удобное для отсчёта значение тока I или напряжения U. По показаниям приборов переменного тока V и mА можно рассчитать полное сопротивление конденсатора

Z = (R2+X2)0,5=U/I , (1)

где R и X = 1/(2*π*F*Cx) - соответственно его активная и реактивная составляющие.

Если потери малы, т. е. R << X, то измеряемая ёмкость определяется формулой

Cx = I/(2*π*F*U).

Схема на рис. 1, а, даёт достаточно точные результаты при измерении больших ёмкостей, сопротивление которых X значительно меньше входного сопротивления вольтметра V.

Схема на рис. 1, б, применяется для измерения меньших ёмкостей, сопротивление которых в десятки и более раз превышает сопротивление миллиамперметра mA. Предположим, что требуется измерять ёмкости в пределах 0,1-1 мкФ на частоте 50 Гц при наличии миллиамперметра переменного тока на 3 мА. Так как сопротивление этих ёмкостей X = 3200...32000 Ом во много раз больше любого возможного сопротивления миллиамперметра, то измерение следует проводить по схеме на рис. 2, б, при напряжении питания U ≥ I*X = 0,003*3200 ≈ 10 В.

Схема на рис. 1, а может быть применена и для измерения ёмкостей электролитических конденсаторов. Если напряжение питания не превышает 1-2 В, то измерение допустимо проводить при установке переключателя В в положение 1. При больших переменных напряжениях возможно повреждение конденсаторов вследствие разложения электролита. Эта опасность устраняется, если переключатель В установить в положение 2. При этом последовательно с источником переменного тока частоты F включается источник постоянного тока, напряжение на зажимах которого U0 должно превышать амплитуду переменного напряжения. Тогда в цепи будет действовать пульсирующее напряжение, безопасное для конденсатора при условии правильной полярности его включения в схему. Пульсирующее напряжение можно также получить при последовательном включении в измерительную схему диода. Во всех случаях вольтметр V и миллиамперметр mA должны измерять лишь переменные составляющие напряжения и тока, для чего они выполняются с закрытой схемой входа.

Измерение ёмкостей методом сравнения (замещения)

Данный метод базируется на сравнении действия, оказываемого измеряемой ёмкостью Сх и известной ёмкостью Со на режим измерительной схемы.

Простейшая схема измерений, в которой ёмкости Сх и Со сравниваются по значению их сопротивления переменному току, приведена на рис. 2. При включении конденсатора Сx потенциометром R устанавливают в цепи ток, удобный для отсчёта или контроля по миллиамперметру переменного тока mA или другому низкоомному индикатору. Затем вместо конденсатора Сx присоединяют к схеме магазин ёмкостей или образцовый (опорный) конденсатор переменной ёмкости и изменением его ёмкости Со добиваются прежнего показания индикатора. Это будет иметь место при Со = Сx. Погрешность измерений зависит от чувствительности индикатора и погрешности отсчёта ёмкости Со; она может быть получена равной примерно 1% и менее.

Рис. 2 Схема измерения ёмкостей

При измерении ёмкостей свыше методом сравнения 5000 пФ схему измерений можно питать от сети переменного тока частотой 50 Гц. Для измерения меньших ёмкостей необходим генератор, работающий на более высоких частотах. Во всех случаях для обеспечения безопасности индикатора в цепь следует включать ограничительный конденсатор (С1) или резистор.

Метод сравнения в различных вариантах широко применяется в мостовых и резонансных измерителях ёмкостей. Он может быть реализован и в микрофарадметрах при существенном снижении погрешности измерений.

http://www.toehelp.ru/theory/toe/lecture01/lecture01.html

megalektsii.ru

Метода - измерение - емкость

Cтраница 1

Методы измерения емкостей двойных слоев подробно изучаются Б электрохимии. Обширный обзор и всесторонняя оценка этих методов имеется ] в книге Фрумкииа, Багоцкого, Иофа и Кабанова Кинетика электродных процессов, Изд. [1]

Методы измерения емкости и индуктивности выбираются, исходя из требуемой точности. С высокой точностью должны быть, например, измерены величины индуктивности и емкости для настраивающихся контуров радиоустройств, с большим допуском ( до 10 %) по точности могут изме ряться индуктивности дросселей и трансформаторов, емкости блокировочных и фильтровых конденсаторов. [2]

Техническими требованиями на конденсаторы установлены методы измерения емкости, обеспечивающие определенную точность измерений. [4]

Изучение изменения поверхности свинцовых электродов методами измерения емкости электрического двойного слоя и по кривым катодной поляризации показало, что поверхность свинцового анода разрыхляется в ходе электролиза. Добавки к электролиту, указанные в таблице 37 и увеличивающие разрушение анодов, также увеличивают и его поверхность, а добавки, уменьшающие разрушение, уменьшают поверхность. [5]

ГОСТами и ТУ на конденсаторы установлены методы измерения емкости, обеспечивающие определенную точность измерений. [6]

Для повышения точности определения влажности целесообразно пользоваться методами измерения емкости, но чувствительными к изменению воли-чины активного сопротивления, напр. [8]

Для повышения точности определения влажности целесообразно пользоваться методами измерения емкости, не чувствительными к изменению величины активного сопротивления, напр, измерением комплексного сопротивления с помощью моста на двух различных частотах с последующим вычислением величины С; измерением мкости с помощью мостов с уравновешиванием двумя параметрами. [10]

Электрохимические процессы образования или удаления адсорбированных атомов водорода п кислорода сильно сокращают или полностью ликвидируют область идеальной поляризуемости на электродах из переходных металлов. Поэтому в подавляющем большинстве случаев метод измерения емкости используется для изучения адсорбции органических веществ на электродах из s, р-металлов. [12]

Широкое применение для защиты металлов от коррозии в кислых средах и при обработке скважин соляной кислотой нашли ингибиторы БА-6 и ГМУ, представляющие собой смесь циклических азотсодержащих соединений. Исследование механизма защитного действия этих ингибиторов методами измерения емкости двойного слоя и снятия электрокапиллярных кривых на электродах показывает, что они, в основном, адсорбируясь на поверхности металла, блокируют его. В результате чего замедляется как катодная реакция ионов водорода, так и анодная реакция ионизации металла. Причем галогенид-ионы в зависимости от заряда поверхности металла обладают синергетическим действием. Установлено, что в начальной стадии растворения стали Ст. [13]

Метод измерения емкости имеет несколько более широкую область применения, чем электрокапиллярный, так как его можно применять на жидких и твердых электродах, хотя необходимо отметить, что на твердых электродах результаты измерения емкости часто искажаются вследствие изменения поверхности. Как и электрокапилляриый метод, он не дает представления о скорости адсорбции поверхностно-активных веществ. Кроме того, в методическом отношении метод измерения емкости переменным током является довольно сложным. [14]

Страницы: 1

www.ngpedia.ru

Измерение емкости методом замещения

Поиск Лекций

Для измерения заданных емкостей С1, С2, С3, или С4 методом замещения собирается схема, приведенная на рис.14. Измеряется значение одной ёмкости в зависимости от варианта задания (см. табл.1).

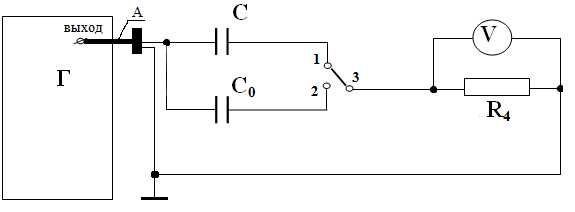
Рис.14. Схема эксперимента при измерении методом замещения;

Таблица 4

Параметры	Измеряемая емкость	Примечания
C1	C2	C3	C4
U1, В		0,009		R4 =5.5 к Ом f4 =1.2 кГц
U2, В		0,031
С0, мкФ		0,05
∆, мкФ
, %

В табл. 4 приняты следующие обозначения:

Оцениваются относительная и абсолютная инструментальные погрешности результата измерения искомой емкости С по формулам:

(15)

(16)

где и - относительная и абсолютная инструментальные погрешности результата измерения;

k - коэффициент, зависящий от принятой доверительной вероятности «Р» и числа слагаемых под корнем «m»;

- относительная погрешность вольтметра V;

- относительная погрешность магазина емкостей;

- относительная погрешность магазина сопротивлений;

- относительная погрешность установки частоты генератора;

- результат измерения искомой емкости;

= = 2,3%.

Погрешность определяется по соотношению (17).

(17)

где Ск – сумма верхних пределов использованных декад магазина емкостей;

С0 – значение набранной на магазине емкости;

- приведенная погрешность, определяемая классом точности магазина емкостей.

=12

Погрешность оценивается соотношением (18)

(18)

где Rk - сумма верхних пределов использованных декад магазина сопротивлений;

R - значение сопротивления, набранного на магазине;

- приведенная погрешность, определяемая классом точности магазина сопротивлений (класс точности используемого магазина 0,2).

=2,8

Погрешность приведена в технических характеристиках генератора ГЗ–112 (см. прил. 6)

= ± 2%

Измерение индуктивности

Измерение индуктивности проводится резонансным методом по схеме, приведенной на рис.15

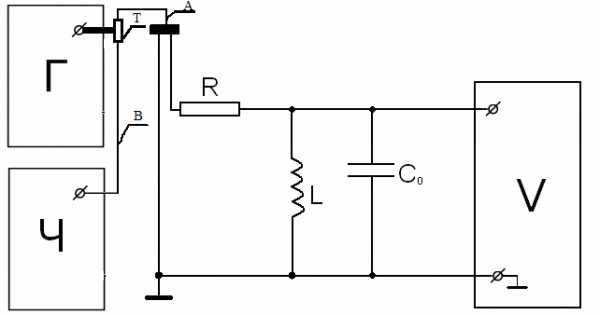
Рис.15. Схема эксперимента при измерении индуктивности.

Приводятся: схема эксперимента; расчетные формулы и таблица с результатами измерений и расчетов (см. табл.5).

Определение искомых величин проводится по формулам:

(19)

L = , (20)

где - значение угловой резонансной частоты;

= 3,14;

f0 - значение циклической резонансной частоты;

L- искомая индуктивность;

С0– заданное значение ёмкости (см. табл.1).

Таблица 5

Результаты экспериментов и расчетов

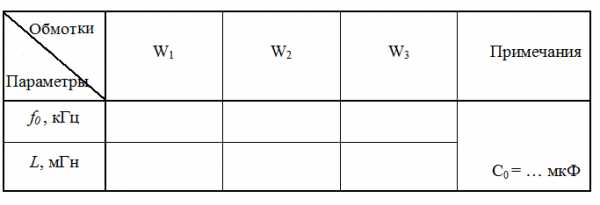
Выводы:

В результате данной лабораторной работы, при проведении измерений переменных электрических напряжений, мы ознакомились с электронными средствами измерений и приобрели навыки их использования.

Библиографический список

1. Миронов Э.Г. Методы и средства измерений: учеб. пособие / Э.Г. Миронов. Екатеринбург: УРФУ, 2013. 356 с.

2. Кузнецов В.А. Метрология. М.: ФГУП «Стандартинформ», 2005. 300 с.

3. Миронов Э.Г., Бессонов Н.П. Метрология и технические измерения: учеб.пособие. М.:КНОРУС, 2015.422с.

4. Левшина Е.С., Новицкий П.В. Электрические измерения физических величин. Измерительные преобразователи: учеб. пособие. Л.:Энергоатомиздат. Ленингр. отделение, 1983. 320 с.

5. Метрология и радиоизмерения: учебник для вузов / Под ред. В.Н. Нефёдова. М.: Высшая школа, 2003. 526 с.

6. РМГ 29 – 99. ГСИ. Метрология. Термины и определения. Рекомендации межгосударственные. Введены с 01 января 2001 года взамен ГОСТ 16263 – 70.

7. ГОСТ 8.417 – 2002. ГСОЕИ. Единицы величин. Введен с 01 сентября 2003 г. взамен ГОСТ 8.417-81.

8. ГОСТ 8.009-84. ГСИ. Нормирование и использование метрологических характеристик средств измерений.

9. ГОСТ 8.508-84. ГСИ. Метрологические характеристики средств измерений и точностные характеристики средств автоматизации ГСП. Общие методы оценки и контроля.

10. ГОСТ 8.401 – 80. ГСИ. Классы точности средств измерений. Общие требования.

11. ГОСТ 8.736 – 2011. ГСОЕИ. Измерения прямые многократные. Методы обработки результатов измер ений. Основные положения.

poisk-ru.ru

Тема: Резонансные методы измерения ёмкости конденсатора

Государственный морской технический университет

Отчёт по лабораторной работе №2

по метрологии

Тема: Резонансные методы измерения ёмкости конденсатора

Выполнил: Яговдик А.Г.

Студент группы 32ИС1

Проверил: Минин В.В.

Санкт-Петербург

2004

Цель лабораторной работы:

Ознакомиться с резонансными методами измерений ёмкостей конденсаторов.
Ознакомиться с методами уменьшения систематической погрешности при резонансных методах измерений.
Получить практические навыки в измерении ёмкости конденсатора.

Общие сведения:

Резонансные методы измерения.

Резонансные методы измерения основаны на определении резонансной частоты измерительного контура, составленного из образцового и измеряемого элементов. Как, известно, резонансная частота колебательного контура определяется выражением:

f0=1/(2П(Lэ∙Сэ)/1/2) (1.1.1.)

где Lэ – эквивалентная индуктивность контура

Сэ – эквивалентная ёмкость контура

Величины эквивалентной ёмкости и индуктивности контура определяются параметрами образцового и измеряемого элементов, входящих в измерительный контур, так и величинам паразитных параметров контура. К таким паразитным параметрам контура относят собственные ёмкости катушек индуктивности ёмкости измерительных приборов, ёмкость монтажа и т.п.

Паразитные параметры измерительного контура являются одним из источником систематических погрешностей измерений резонансными методами. Рассмотрим резонансные методы измерений, анализируя и постепенно устраняя возможные систематические погрешности, обусловленные методом измерения и способом получения результата.

1.2 Измерение ёмкости конденсатора.

Наиболее простым резонансным методом измерения ёмкости конденсатора является метод, основанный на измерении резонансной частоты измерительного контура, состоящий из образцовой катушки индуктивности и измеряемого конденсатора. Упрощённая эквивалентная схема измерений для этого случая представлена на рис. 1.2.1.

На рис.1.2.1. обозначены

ГВЧ – генератор высоких частот

Lоб – образцовая катушка индуктивности

Сx – измеряемый конденсатор

V – индикатор резонанса

Измерительный контур настраивают на резонанс по максимальным показаниям индикатора резонанса путём изменения частоты сигнала ГВЧ. Фиксируют значения резонансной частоты f0.

Сx=1/(4П2∙f02∙Lоб) (1.2.1.)

где f0 резонансная частота колебательного контура

Lоб – индуктивность образцовой катушки.

Из сопоставлений выражений 1.1.1 и 1.2.1 видно, что в этом случае считают, что эквивалентная индуктивность контура Lэ= Lоб и Сэ=Cоб , т.е. пренебрегают наличием паразитных параметров контура, что в этом случае является основным источником систематической погрешности.

Основными паразитными параметрами измерительного контура являются: собственная ёмкость образцовой катушки индуктивности – СL , ёмкость монтажа CM , входная ёмкость индикатора резонанса – Си . Эквивалентная схема измерения ёмкости с учётом основных паразитных параметров измерительного контура представлена на рис. 1.2.3.Из приведённой схемы видно, что ёмкости СL CMСи включены параллельно измерительному контуру.

Следовательно, эквивалентная ёмкость измерительного контура должна определяться как:

СЭ=СХ+СL+CM+CИ=Сх+СП (1.2.2.)

Где СN – паразитная ёмкость измерительного контура.

Подставив (1.2.2) в (1.1.1) и решив его относительно СХ получим:

СХ = (1/(4П2∙f02∙ Lоб))-Сп (1.2.3)

Величина собственной ёмкости образцовой катушки является одним из её метрологических параметров и указывается на её корпусе (единицы пФ). Ёмкость монтажа CM определяется длиной и взаимным расположением соединительных проводов и элементов измерительного контура (единицы десятки пФ). Ёмкость измерителя (Си) определяется входной ёмкостью индикатора резонанса и ёмкостью соединительного кабеля (десятки-сотни пФ). Суммарная величина паразитной ёмкости измерительного контура может быть определена экспериментальна. Для этого необходимо измерительный контур с подключённой катушкой индуктивности и без измеряемоё емкости настроить на резонанс по максимальным показаниям индикатора резонанса путём изменения частоты сигнала ГВЧ и определить собственную резонансную частоту измерительного контура f0 ИК. Паразитная ёмкость измерительного контура может быть определена в соответствии с выражением:

СП=1/(4П2∙ f02 ИК ∙ Lоб) (1.2.4.)

В этом случае, если значение паразитных ёмкостей известно или определено путём измерений, как это описано выше, то использование выражения (1.2.3)позволяет существенно уменьшить величину систематической погрешности измерения величины Сх.

Однако, следует отметить, что представление паразитных параметров измерительного контура в виде элементов с сосредоточенными параметрам лишь приблизительно, т.к. СL является распределённой по обмотке образцовой катушки, СМ по измерительному контуру, а СИ – частично по кабелю индикатора резонанса. Кроме того, неученой остаётся паразитная индуктивность проводов, активные сопротивления потерь в элементах и проводах контура. Любая замена схем с распределёнными параметрами эквивалентными схемами с сосредоточенными параметрами влечёт за собой зависимость этих параметров от частоты. Поэтому учёт паразитных параметров (Сп), определённых на собственной резонансной частоте измерительного контура (f0 ИК), при измерениях на других частотах является источником систематической погрешности измерений. Чтобы ещё более уменьшить систематическую погрешность измерений применяют метод замещения.

Метод замещения

В соответствии с методом замещения измерения осуществляются в два этапа:

1. Измерительный контур, состоящий из образцовой катушки измеряемой ёмкости, настраивают в резонанс по максимальным показаниям индикатора резонанса путём изменения частоты сигнала ГВЧ.

2. Не меняя настройки частоты ГВЧ, отключают измеряемую ёмкость Сх и подключают вместо неё к измерительному контуру образцовый конденсатор переменной ёмкости Соб. Настраивают измерительный контур в резонанс по максимальному отклонению индикатора резонанса путём изменения ёмкости образцового конденсатора. По градуированной шкале образцового конденсатора определяют резонансное значение Соб. Схема измерений ёмкости методом замещения представлена на рис.1.2.3..

Очевидно, что при первой настройке контура в резонанс резонансная частота

f0=1/(2П(LЭ∙(СХ+СП))1/2)

а при второй

f0=1/(2П(LЭ∙(СОБ+СП))1/2)

т.к. частота генератора не измена при обоих измерениях, то СХ=СОБ (1.2.5.)

и паразитные параметры измерительного контура не оказывают влияния на точность измерений.

При измерении методом замещения систематическая погрешность может быть вызвана тем, что при отключении СХ и подключении образцового конденсатора изменяется ёмкость монтажа.

Эту погрешность тоже можно уменьшить применяя метод компенсации.

Метод компенсации

При измерении ёмкости методом компенсации измерения производятся в два этапа:

Измерительный контур, состоящий из образцовой индуктивности LОБ , измеряемой ёмкости СХ и образцового конденсатора рис.(1.2.4) настраивают в резонанс по максимальным показаниям индикатора резонанса путём изменения частоты сигнала ГВЧ. При этом значение ёмкости образцового конденсатора СОБ1 должно быть выбрано вблизи минимального и определено по градуированной шкале образцового конденсатора.
Не меняя частоты настройки ГВЧ, отключают измерительную ёмкость СХ и настраивают контур в резонанс на той же частоте путём компенсации отключённой ёмкости СХ увеличением ёмкости СОБ. Определяют резонансное значение СОБ2 по градуированной шкале образцового конденсатора.

При первой настройке измерительного контура на резонанс

f0=1/(2П(LЭ∙(СХ+СОБ1+СП))1/2)

а при второй

f0=1/(2П(LЭ∙(СХ+СОБ1+СП))1/2)

Т.к. частота генератора неизменна при обоих измерениях, то

CХ= СОБ2-СОБ1 (1.2.6.)

И паразитные параметры измерительного контура не оказывают влияния на результаты измерений.

Лабораторная установка

Лабораторная установка состоит из генератора высокой частоты (ГВЧ), измерительного контура, индикатора настройки контура в резонанс. Измерительный контур смонтирован на плате лабораторного стола и состоит из клемм для измерительных и образцовых элементов, ГВЧ и индикатора резонанса. Кроме же того на этой плате смонтировано разделительное сопротивление ® и образцовый конденсатор переменной ёмкости (СОБ) с тумблером (К), позволяющим подключить его к измерительному контуру.

gigabaza.ru

Способ измерения емкости

(72) Автор . изобретения

Б. И. Губский (Vl ) Заявитель (S4) СПОСОБ ИЗМЕРЕНИЯ ЕМКОСТИ

Изобретение относится к электроизме ритепьной технике, в частности к измере"нию емкости в тех случаях, когда необходимо использовать напряжения и токи очень малой амплитуды, например,. при измерении емкости сегнемоэлектрических конденсаторов.

Известны способы измерения емкости в мостовых схемах; когда измеряемую емкость включают в одно из плеч мссто вой схемы и по степени разбаланса Мос та судят о знаЧении измеряемой емкостя (И

Недостатком данных способов являет ,ся необходимость пропускания тока через исследуемый объект, под действием коте рого изменяются параметры объекта, а, 15 следовательно, снижается точность изме рения.

Наиболее близким к предлагаемому яв ляется способ измерения емкости, осло

20 ванный на измерении теплового шума ре зистора, подключенного параллельно ис следуемому объекту, и измерении абсо лютной температуры (2) .

Значение емкости затем рассчитывают с ислопьэованием формулы Найквиста по результатам "измерения теплового шума .. при различных,сопротивлениях калиброванныхх резисторов. При этом нет необходимости прикладывать к исследуемому объекту напряжение извне.

Недостатками известного способа являются значительная трудоемкость s проведении опытов и большие затраты времени на обработку результатов измерений. цепь изобретения. - ловы)пение быстродействия.

Поставленная цепь достигается тем, что измеряют в широкой полосе частот максимальную величину теплового шума .лри изменении сопротивления резистора, а о величине емкости судят по формуле

С=кт!бают, где и - постоянная Бопьцмана;

Т - абсолютная температура резистора;

О среднее значение квадрата наma пряжения максимального ypos ня теплового шума. (1) зо (4) допуская, что fz/ -

3 9171

Предлагаемый способ измерения емкости заключается в спедуюшем.

К измеряемой емкости С параллельно подкпючают переменный резистор. При определенном значении сопротивпения ре зисторв напряжение теплового шума 0 нв кпеммах резистора будет максимальным, так квк величина этого напряжения

62 зависит от вепичины сопротивпения реас р. Сопротнвпэние ре упру с попучения максимапьного напряжения теплового шума 0 на его зажимах, а на»

2 пряженне теплового шума 0 измеряют в широкой полосе частот при большом соотношении граничных частот в полосе - И уси пения. Затем, испоиьзуя математическую зависимость максимального значения напряжения тецповаго шума 0 в ши-г рокой поносе частот на резисторе, зашун тированном емкостью С, определяют зна- 26 чение этой емкости.

Предлагаемый способ основан на следующих теоретических предпосыцках.

Согласно теореме Найквиств средний квадрат напряжения тецпового Шума U 25 иа зажимах цепи, состоящей из вкпючен них параппецьно сопротивпения R и емкости С, опредепяется в виде г

4 - (arctg+CR -ar ctg Q, сЦ, 2БС

Максимуму значению Ф в (1) при постоянных rdq М и C соответствует вы . З бор оптимального сопротивпения, равного

1 где Ц, т вЂ” линейные граничные частоты в Гц.

Подставпяя (2) и (1) нопучим

U „- -(а-4 вгсйд /Х)

z значение емкости в виде

28 4

В реальных усповнях 4/>1 не может быть бесконечно большим, однако можно показать, что возникающую прн этом погрешность измерения max, а значит и

С, можно снизить до значения 0,1-0,3% прн испоцьзовании мвлошумяших попевых транзисторов во входном каскаде н принятии специальных мер по подавиенню собственных шумов усипитепя теплового шумва

Испопьзование предлагаемого способа позволяет быстро, просто и с достаточно высокой точностью измерять емкость исследуемых объектов при однократном измерении теплового шума без приложения к ним напряжения и в отсутствии тока, протекакицего через них, что черезвычай но важно в ряде научных нсспедований.:

Предлагаемый способ прост в реапнэвцни и позвопяет создать прибор с прямым отсчетом значения измеряемой емкости. При етом трудоемкость измерений и затраты времени нв обработку результатов еще более снижаются.

Формула изобретения

Способ измерения емкости, основанный иа измерении теплового шума резистора, подкшоченного параплепьно исспедуемому объекту н, измерении абсолютной температуры, о т н и ч а ю щ и йс я тем, что, с целью повышения быстродействия, измеряют в широкой полосе частот максималpную вепнчину теппового шума прн изменении сопротивпения резистора„а о вепичине емкости судят по формуле

KT с =.- вЂ”.

max где к - постоянная Больцмана;

Ц среднее значение квадрата напряжения макснмапьного уровня теплового шума;

Т - абсолютная температура резистора.

Источники информации, принятые во внимание при экспертизе

1. Электрические измерения. Под ред.

° Е. Г. Шрамкова. М., Высшая школа".

1972, с. 281-288.

2. Вгоопц 73. Лцсйи,ation phenomena in

Мыз,4t d Sy ВиЧезя а.И. Асадепйс Press" нем МоФ, 1965,. р. 12«19.

ВНИИПИ Заказ 1882/66 Тираж 719 Подписное

Филиал ППП Патент, r. Ужгород, ул. Проектная, 4