ул.Симферопольская
дом 5, офис 9
![]() Корзина
Корзина
Корзина пуста
1.1 Методы анализа, основанные на законах Ома и Кирхгофа. Примеры решения задач закон кирхгофа
Примеры решения задач на законы Кирхгофа
Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.
Задача 1
Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.
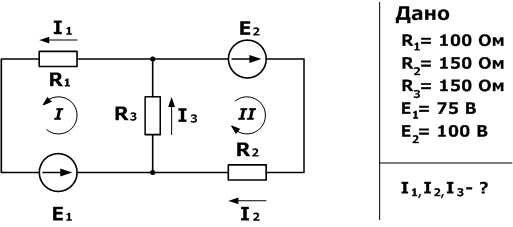
Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.
Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи
Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.
Уравнения для первого и второго контуров по второму закону будут:
Все эти три уравнения образуют систему
Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).
Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.
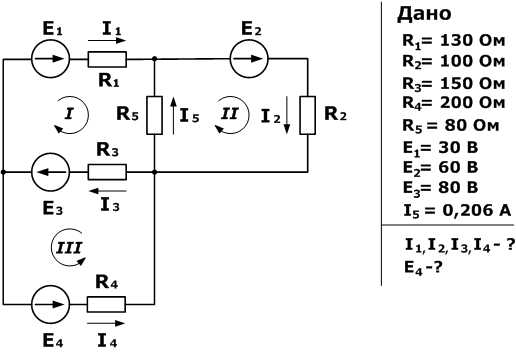
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
На основании этих уравнений составляем систему с 5-ью неизвестными
Решив эту систему любым удобным способом, найдем неизвестные величины
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Читайте также - расчет простых цепей постоянного тока
www.electroandi.ru
Методы анализа, основанные на законах Ома и Кирхгофа
Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях → 1.1 Методы анализа, основанные на законах Ома и Кирхгофа Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряженияхЗакон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Решение задач на закон Ома и законы КирхгофаЗадача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка – потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
Rab=R1⋅R3R1+R3+ (R47+R5+R6)⋅R2 (R47+R5+R6)+R2.
2. При замкнутом ключе К
R47=R1⋅R3R1+R3+R47⋅R2R47+R2,
где
R47=R4⋅R7R4+R7.
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.
Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
Рис. 1.3
1. При разомкнутом ключе К
Rab= (R1+R3)⋅ (R2+R4) (R1+R3)+ (R2+R4).
2. При замкнутом ключе К
Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.
Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rl и R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
Rab=1Yab=11R1+1R2+1R3.
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофа определяется как функция тока I (показание амперметра).
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.
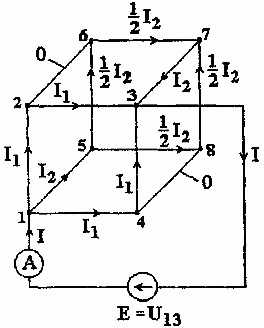
Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 – 6 и 4 – 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.
Откуда:
I1=32I2; I2=23I1.
А значит, общий ток
I=2I1+I2=2I1+23I1=83I1.
Но
U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.
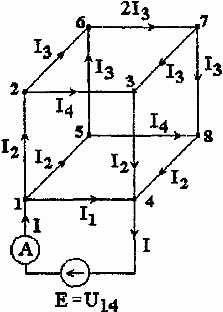
Рис. 1.8
В силу симметрии токи в ребрах 1 – 2, 1 – 4, 2 – 3 и 4 – 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 – 6 и 4 – 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,
то, сокращая на R, имеем:
I4=4I3
или
I3=14I4.
Ток
I2=I3+I4=14I4+I4=54I4
или
I4=45I2.
Но
U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.
Откуда, сокращая на R, имеем:
I1=145I2
или
I2=514I1.
Но
U14=I⋅R14= (I1+2I2)⋅R14= (I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.
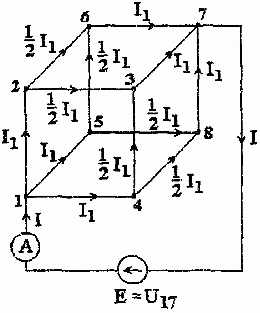
Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.
Откуда искомое сопротивление R17 = 5/6·R.
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10, а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?
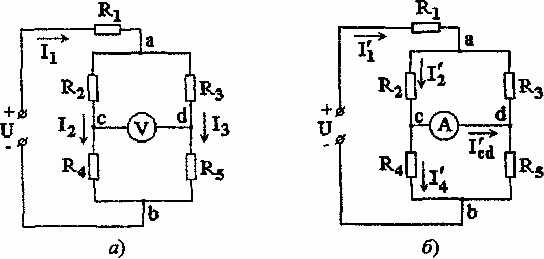
Рис. 1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
R=R1+ (R2+R4)⋅ (R3+R5) (R2+R4)+ (R3+R5)=10+75⋅50125=40 Ом.
В неразветвленной части цепи протекает ток
I1=UR=12040=3 A.
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
I2=I1⋅R3+R5 (R2+R4)+ (R3+R5)=3⋅50125=1,2 A;I3=I1⋅R2+R4 (R2+R4)+ (R3+R5)=3⋅75125=1,8 A.
2. Найдем напряжение на зажимах параллельных ветвей:
Uab=I1⋅ (R2+R4)⋅ (R3+R5) (R2+R4)+ (R3+R5)=3⋅75⋅50125=90 B.
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U – R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15 B.
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.
Искомый ток, проходящий через амперметр,
IA=I′cd=I′2−I′4=2447=0,51 A.
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.
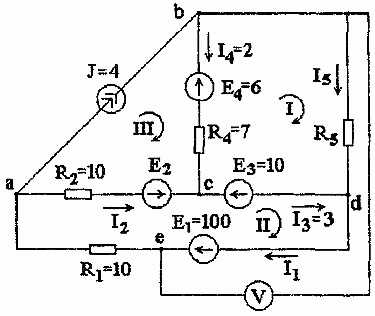
Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 – три, неизвестных величин E2 и R5 – две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.
Из первых трех уравнений находим токи:
I5=J−I4=4−2=2 A;I1=I5+I3=2+3=5 A;I2=−J+I1=−4+5=1 A.
из четвертого уравнения
R5=E3+E4+I4⋅R4I5=10+6+142=15 Ом.
Величину E2 определяем из последнего уравнения:
E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
φe=φa−I1⋅R1=0+5⋅10=50 B;φd=φe−E1=50−100=−50 B;φb=φd+I5⋅R5=−50+2⋅15=−20 B.
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс – сопротивления участков (рис. 1.12).
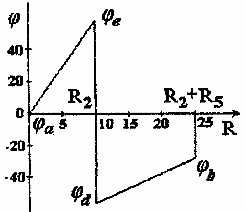
Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.
4. Произведем проверку баланса мощностей:
Pисточников=E1⋅I1+E2⋅I2+E3⋅ (−I3)+E4⋅ (−I4)+Uba⋅J;Pпотребителей=I12⋅R1+I22⋅R2+I42⋅R4+I52⋅R5.
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого
Pисточников=100⋅5+ (−30)⋅1+10⋅ (−3)+6⋅ (−2)+ (−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.
Закон Ома, законы Кирхгофа в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачивторой закон Кирхгофа, первый закон Кирхгофа, Законы Кирхгофа, закон Ома
16.10.2011, 65757 просмотров.
rgr-toe.ru
Решение задач на закон Ома и законы Кирхгофа
Методы анализа, основанные на законах Ома и законах Кирхгофа
Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка – потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
Rab=R1⋅R3R1+R3+(R47+R5+R6)⋅R2(R47+R5+R6)+R2.Rab=R1⋅R3R1+R3+(R47+R5+R6)⋅R2(R47+R5+R6)+R2.
2. При замкнутом ключе К
R47=R1⋅R3R1+R3+R47⋅R2R47+R2,R47=R1⋅R3R1+R3+R47⋅R2R47+R2,
где
R47=R4⋅R7R4+R7.R47=R4⋅R7R4+R7.
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.
Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
Рис. 1.3
1. При разомкнутом ключе К
Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).
2. При замкнутом ключе К
Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.
Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rlи R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
Rab=1Yab=11R1+1R2+1R3.Rab=1Yab=11R1+1R2+1R3.
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофаопределяется как функция тока I (показание амперметра).
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.

Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 – 6 и 4 – 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.
Откуда:
I1=32I2; I2=23I1.I1=32I2; I2=23I1.
А значит, общий ток
I=2I1+I2=2I1+23I1=83I1.I=2I1+I2=2I1+23I1=83I1.
Но
U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.

Рис. 1.8
В силу симметрии токи в ребрах 1 – 2, 1 – 4, 2 – 3 и 4 – 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 – 6 и 4 – 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,
то, сокращая на R, имеем:
I4=4I3I4=4I3
или
I3=14I4.I3=14I4.
Ток
I2=I3+I4=14I4+I4=54I4I2=I3+I4=14I4+I4=54I4
или
I4=45I2.I4=45I2.
Но
U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.
Откуда, сокращая на R, имеем:
I1=145I2I1=145I2
или
I2=514I1.I2=514I1.
Но
U14=I⋅R14=(I1+2I2)⋅R14=(I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.U14=I⋅R14=(I1+2I2)⋅R14=(I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.

Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.
Откуда искомое сопротивление R17 = 5/6·R.
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10,а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?

Рис. 1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
R=R1+(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=10+75⋅50125=40 Ом.R=R1+(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=10+75⋅50125=40 Ом.
В неразветвленной части цепи протекает ток
I1=UR=12040=3 A.I1=UR=12040=3 A.
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
I2=I1⋅R3+R5(R2+R4)+(R3+R5)=3⋅50125=1,2 A;I3=I1⋅R2+R4(R2+R4)+(R3+R5)=3⋅75125=1,8 A.I2=I1⋅R3+R5(R2+R4)+(R3+R5)=3⋅50125=1,2 A;I3=I1⋅R2+R4(R2+R4)+(R3+R5)=3⋅75125=1,8 A.
2. Найдем напряжение на зажимах параллельных ветвей:
Uab=I1⋅(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=3⋅75⋅50125=90 B.Uab=I1⋅(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=3⋅75⋅50125=90 B.
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U – R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15 B.UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15 B.
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.
Искомый ток, проходящий через амперметр,
IA=I′cd=I′2−I′4=2447=0,51 A.IA=I′cd=I′2−I′4=2447=0,51 A.
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.

Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 – три, неизвестных величин E2 и R5 – две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.
Из первых трех уравнений находим токи:
I5=J−I4=4−2=2 A;I1=I5+I3=2+3=5 A;I2=−J+I1=−4+5=1 A.I5=J−I4=4−2=2 A;I1=I5+I3=2+3=5 A;I2=−J+I1=−4+5=1 A.
из четвертого уравнения
R5=E3+E4+I4⋅R4I5=10+6+142=15 Ом.R5=E3+E4+I4⋅R4I5=10+6+142=15 Ом.
Величину E2 определяем из последнего уравнения:
E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
φe=φa−I1⋅R1=0+5⋅10=50 B;φd=φe−E1=50−100=−50 B;φb=φd+I5⋅R5=−50+2⋅15=−20 B.φe=φa−I1⋅R1=0+5⋅10=50 B;φd=φe−E1=50−100=−50 B;φb=φd+I5⋅R5=−50+2⋅15=−20 B.
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс – сопротивления участков (рис. 1.12).

Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.
4. Произведем проверку баланса мощностей:
Pисточников=E1⋅I1+E2⋅I2+E3⋅(−I3)+E4⋅(−I4)+Uba⋅J;Pпотребителей=I21⋅R1+I22⋅R2+I24⋅R4+I25⋅R5.Pисточников=E1⋅I1+E2⋅I2+E3⋅(−I3)+E4⋅(−I4)+Uba⋅J;Pпотребителей=I12⋅R1+I22⋅R2+I42⋅R4+I52⋅R5.
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого
Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.
toe.umi.ru
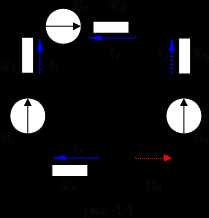
8. Задания по законам Кирхгофа
1
2
3
4
7
10
5
8
11
6
9
9. Примеры решения задач Пример 1
1. Дана электрическая цепь постоянного тока. Необходимо найти эквивалентное сопротивление RЭКВИВ.
Для этого на параллельно соединенных резисторах R3 и R4 найдем их общее сопротивление: их произведение разделим на их сумму:
R34 = (R3 ∙ R4) / (R3 + R4)
Затем точно также на параллельных участках R6 и R7 найдем их общее сопротивление
R67 = (R6 ∙ R7) / (R6 + R7)
Резисторы R2 и R34 соединены последовательно, значит, их надо сложить:
R2+ R34 = R234
Резисторы R234 и R5 соединены параллельно. Поэтому (как для двух параллельных) их произведение разделим на их сумму:
R2345 = (R234 ∙ R5) / (R234 + R5)
Получаем, что резистор R1 и эквивалентно рассчитанные участки сопротивлениями R2345 и R67 соединены последовательно, их сложим и найдем полное сопротивление, т. е. эквивалентное сопротивление всей цепи:
RЭКВИВ = R1 + R2345 + R67
2. Зная напряжение (или ток), подведенное к цепи, найдем ток (или напряжение) цепи из закона Ома для участка цепи. U = I∙ R или I = U / R
3. Т. к. участки с сопротивлениями R1, R2345 и R67 соединены последовательно, то ток на этих участках одинаков:
I1 = I2345 = I67 = I
Значит, можем найти напряжение на этих же участках, умножив ток (ток одинаков на последовательных участках цепи!) на сопротивления участков.
U1 = I1∙ R1
U2345 = I1∙ R2345 = U234 = U5, т. к. на параллельных участках цепи напряжение одинаково.
U67 = I1∙ R67 = U6 = U7 , т. к. на параллельных участках цепи напряжение одинаково.
Зная напряжения на резисторе R5 и участке R234, найдем токи на них: I5 = U5 / R5 ; I234 = U234 / R234
Аналогично (заметьте, напряжение на них одинаково, но сопротивление разное, поэтому и токи разные!): I6 = U6 / R6; I7 = U7 / R7
Проверка: А) должно быть, чтобы сумма токов I6 и I7 равно току I67 на этом участке с сопротивлением R67, согласно первому закону Кирхгофа. I67 = I6 + I7
Б) должно быть, чтобы сумма токов I234 и I5 равно току I2345 на этом участке с сопротивлением R2345, т. е. I2345 = I234 + I5
Но токи на последовательно соединенных участках R2 и R34 цепи одинаковы,
т. е. ток I2 равен току на I34, но I34 = I3 + I4. Запишем это:I2 = I34 = I3 + I4
5. Напряжения на последовательно соединенных участках R2 и R34 цепи равно сумме напряжений
U234 = U2 + U34 . Но U34 = U3 = U4
Зная ток I2 на R2, найдем напряжение U2 на нем U2 = I2∙ R2
Также, зная ток I34, найдем напряжение U34 на участке U34 = I34∙ R34
Проверка. Должно быть, что напряжения U34 = U3 = U4 , т. к. напряжение на параллельных участках одинаково. Отсюда найдем из закона Ома токи на резисторах R3 и R4.
6. Остается найти мощности на всей цепи и на отдельных участках по любой из известных формул мощности: Рi = Ii ∙ Ui или Рi = Ii2 ∙ Ri
Задача решена в общем виде.
studfiles.net
Первый закон Кирхгофа, теория и примеры
Допустим, что у нас имеется произвольная разветвленная сеть проводников. В отдельных участках включены разнообразные источники тока. ЭДС источников постоянны и будем считать известными. При этом токи во всех участках цепи и разности потенциалов на них можно вычислить при помощи закона Ома и закона сохранения заряда.
Для упрощения решения задач по расчетам разветвлённых электрических цепей, имеющих несколько замкнутых контуров, несколько источников ЭДС, используют законы (или правила) Кирхгофа. Правила Кирхгофа служат для того, чтобы составить систему уравнений, из которой находят силы тока в элементах сложной разветвленной цепи.
Каждую точку разветвления цепи, в которой сошлось три или более проводников, по которым текут токи, называют узлом (рис.1).
Обычно принято считать, что если ток в узел входит, то ток положительный, выходящий из узла ток является отрицательным. Однако, может быть наоборот, главное следует считать, что токи, идущие к точке разветвления и исходящие от разветвления токи, имеют противоположные знаки. При составлении суммы токов, часто на схемах силы токов изображают стрелками с направлениями от узла или к узлу.
Формулировка первого закона Кирхгофа
Сумма токов в узле цепи с учетом их знаков равна нулю:
Первое правило Кирхгофа является следствием закона сохранения электрического заряда. Алгебраическая сумма токов, сходящихся в любом узле цепи – это заряд, который приходит в узел за единицу времени. Если в рассматриваемой точке токи не изменяются во времени, то сумма токов равна нулю, так как в противном случае потенциал нашего узла изменялся бы, следовательно, токи были бы переменными. При установившемся постоянном токе ни одна из точек проводника, ни какой его участок цепи не накапливают электрический заряд. Иначе токи в цепи не были бы постоянными.
Первый закон Кирхгофа еще называют правилом узлов.
Примеры решения задач
ru.solverbook.com
Решение задач по методу Кирхгофа
§ 4. Решение задач по методу Кирхгофа
етоды изученные в предыдущих параграфах позволяют решить любую схему. Но чем сложнее схема, тем с большим количеством преобразований придется столкнуться. К примеру, сначала схему необходимо будет свернуть до одного контура, найти необходимые значения, затем постепенно её разворачивать производя все новые и новые вычисления.
Это достаточно неудобно, и хотя закон Ома доказал свою универсальность, со временем стали появляться и другие более удобные методы. Основой для каждого из методов служит базисный закон – закон Георга Ома.
Густав Роберт Кирхгоф (1824-1887), профессор физики Гейдельберского университета в Берлине, в 1846 году установил два правила, названные в его честь[18] – «Первое и Второе правило Кирхгофа для электрических цепей»[19].
§ 4.1. Первый закон Кирхгофа
Первый закон Кирхгофа. Алгебраическая сумма токов в любом узле равна нулю.
При выведении первого закона Кирхгоф опирался на закон сохранения электрического заряда[20]. Если в разветвление X, проводящей цепи входит ток силой I, а выходят токи I1 и I2, за время ∆t в область разветвления втекает электрический заряд , а вытекает заряд . Приравнивая эти величины, друг к другу находим:
Если же в узле сходится n проводников, то
где под Ii понимают алгебраическую величину силы тока, которая берется со знаком «плюс», если ток входит в узел, и со знаком «минус» если выходит. Это правило называется правилом знаков.
Таким образом, мы получаем, что в один узел не могут втекать все токи из прилегающих ветвей, и из одного узла не могут вытекать все токи. Так как это нарушит закон сохранения заряда.
§ 4.2. Второй закон Кирхгофа для участка цепи.
Как уже говорилось, законы Кирхгофа включают в себя закон Ома. И второй закон для участка цепи[21] является прямым следствием закона Ома. Известно, что электрическое напряжение есть разница электрических потенциалов между двумя точками. Тогда, пусть электрические потенциалы в концевых точках участка цепи AB c сопротивлением R есть и рис 4.2. Тогда, по определению напряжения U на участке АВ,
а закон Ома приобретает вид:
Когда на участке AB имеется источник тока с ЭДС E, разность потенциалов изменяется на величину , где знак выбирается в зависимости от полярности включения источника (по току или против него). Тогда соотношение 4.4 принимает вид:
Если цепь сложная рис 4.3, то на пути от точки А к точке В может встретиться m источников тока ЭДС Ei и n сопротивлений Rk, по которым протекают токи Ik. Тогда второй закон Кирхгофа для участка цепи записывается так:
Из соотношения 4.6 выразим силу тока:
В такой записи это соотношение получило название обобщенный закон Ома. Для электрической схемы изображенной на рисунке 4.3 сила тока по обобщенному закону Ома будет выглядеть так:
§ 4.3. Второй закон Кирхгофа для замкнутого контура.
Второй закон Кирхгофа для замкнутого контура. В любом контуре электрической цепи алгебраическая сумма ЭДС, источников напряжения, равна алгебраической сумме падений напряжения вдоль этого контура.
Второй закон Кирхгофа для замкнутого контура также основан на законе Ома и законе сохранения энергии – в замкнутой системе, сколько энергии излучается, столько же энергии и поглощается, таким образом, общее количество энергии остается неизменным.
 Возьмем, к примеру, электрическую схему изображенную на рисунке 4.4. Стрелкой в верхнем левом углу обозначен обход контура. Обычно, но не обязательно, его направление выбирается по часовой стрелке. Обход необходим для правильного составления уравнения, так как при записи уравнений по второму[22] закону Кирхгофа используется следующее правило знаков:
Возьмем, к примеру, электрическую схему изображенную на рисунке 4.4. Стрелкой в верхнем левом углу обозначен обход контура. Обычно, но не обязательно, его направление выбирается по часовой стрелке. Обход необходим для правильного составления уравнения, так как при записи уравнений по второму[22] закону Кирхгофа используется следующее правило знаков:
Если заданные или выбранные направления ЭДС, напряжений и токов в ветвях совпадают с обходом контура, то ЭДС в суммах слева, напряжения и токи в суммах справа записывают со знаком «плюс», если не совпадают с обходом контура – со знаком «минус».
Теперь составим уравнение для принципиальной электрической схемы, изображенной на рис 4.4. Направление токов выбрано совершенно случайно, только для этого примера.
§ 4.3. Метод решения задач на основе законов Кирхгофа.
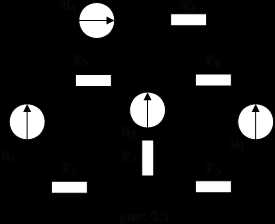 Для того чтобы уметь применять законы Кирхгофа решим трех контурную электрическую цепь изображенную на рис. 4.5.
Для того чтобы уметь применять законы Кирхгофа решим трех контурную электрическую цепь изображенную на рис. 4.5.
vunivere.ru
2.5.1. Метод непосредственного применения законов Кирхгофа
Пример . Методом непосредственного применения законов Кирхгофа рассчитать токи в схеме на рис.
Число ветвей обозначим m, а число узлов n. Произвольно выбираем положительные направления токов в ветвях и направления обхода контуров. Поскольку в каждой ветви протекает свой ток, то число токов, которое следует определить, а следовательно, и число уравнений, которое нужно составить, равно m. По первому закону Кирхгофа составляем n-1 уравнений. Недостающие m-(n-1) уравнений следует составить по второму закону Кирхгофа для взаимно независимых контуров.
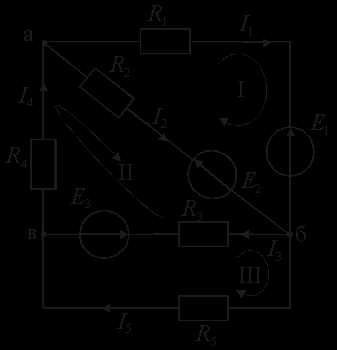 Рис. 2.20. Схема замещения сложной электрической цепи с несколькими источниками энергии: I, II, III – номера контуров
Рис. 2.20. Схема замещения сложной электрической цепи с несколькими источниками энергии: I, II, III – номера контуров
1. Проводим топологический анализ.
Она содержит пять ветвей и три узла, m = 5, n = 3. Составляем два уравнения по первому закону Кирхгофу, т. к. n – 1 = 2 (например, для узлов а и б).
2. Составляем уравнения по певому и второму законам Кирхгофа
Для узла "а" - I1 - I2 + I4 = 0.
Для узла "б" - I1 + I2 - I3 - I5 = 0.
Остальные m - (n - 1) = 3 уравнения составляем по второму закону Кирхгофа.
Для контура I - R1·I1 - R2·I2 = - E1 + E2.
Для контура II - R2·I2 + R3·I3 + R4·I4 = - E2 - E3.
Для контура III - - R3·I3 + R5·I5 = E3.
Решив систему, состоящую из пяти уравнений, находим пять неизвестных токов. Если какие-либо значения токов оказались отрицательными, то это означает, что действительные направления этих токов противоположны первоначально выбранным.
При расчётах сложных цепей с использованием ЭВМ удобна матричная форма записи. Уравнения, составленные по законам Кирхгофа, запишем в виде
- I1 - I2 + 0 + I4 + 0 = 0
I1 + I2 - I3 + 0 - I5 = 0
R1·I1 - R2·I2 + 0 + 0 + 0 = - E1 + E2
0 + R2·I2 + R3·I3 + R4·I4 + 0 = - E2 - E3
0 + 0 + - R3·I3 + 0 + R5·I5 = E3.
В матричной форме
или [R]·[I] = [Е],
где [R] – квадратная (5 х 5) матрица, элементами которой являются коэффициенты при неизвестных токах в исходных уравнениях;
[I] – матрица - столбец неизвестных токов;
[E] – матрица - столбец, элементами которой могут быть алгебраическая сумма ЭДС.
Решение матричного уравнения ищут в виде
[I] = [R]-1·[E],
где [R]-1 – матрица, обратная матрице [R].
Рассмотренный метод расчета неудобен, если в цепи имеется большое количество узлов и контуров, поскольку потребуется решать громоздкую систему уравнений. В таких случаях рекомендуется применять метод контурных токов, позволяющий значительно сократить число расчетных уравнений 2.
Метод контурных токов
Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.
Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).
Эта схема эквивалентна, если
а)E = IZiI;
б) ZiII = ZiI.
1) Топологический анализ схемы.
а) Как и в предыдущем методе, определяют число ветвей b.
б) Определяют число узлов у.
в) Подсчитывают число независимых контуров Nk = b – y + 1.
Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.
Все контуры нумеруют и каждому контуру присваивают свой контурный ток: Ik1; Ik2;IkNk.
За положительное направление контурного тока принимают положительное направление обхода контура.
2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений Nk = Nkпорядка:
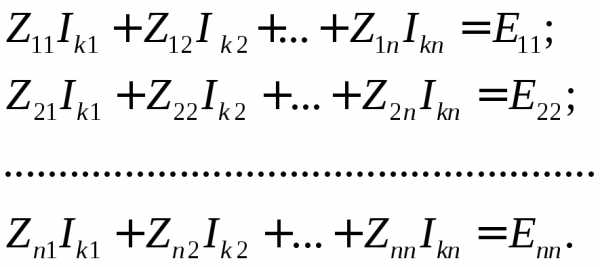
где Iki– контурный токi-го контура;
Zii– собственное сопротивлениеi-го контура и равно алгебраической сумме сопротивлений, входящих вi-й контур;
Zji– сопротивление смежных ветвей междуi-м иj-м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;
Eki– контурная ЭДСi-ого контура. Она равна алгебраической сумме ЭДС, входящих вi-й контур. Контурная ЭДСEkiберется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.
3) По правилу Крамера находят контурные токиIki= .
.
4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. В алгебраической сумме контурные токи берутся со знаком «+» , если ток ветви и совпадает с контурным током и «–» если не совпадает.
Если токи ветви оказались положительными, то выбранное направление тока совпадает с истинным и наоборот.
Пример.Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.
1. Проводим топологический анализ
а) b= 6; б)y= 4;в)Nk= 6 – 4 + 1=3.
2) Составим систему уравнений по методу МКТ
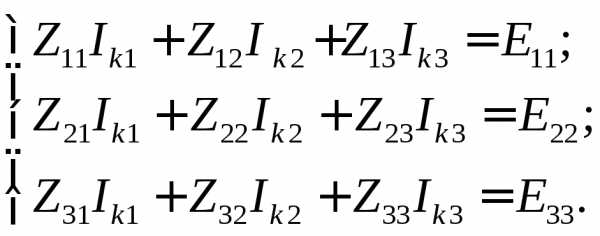
где: 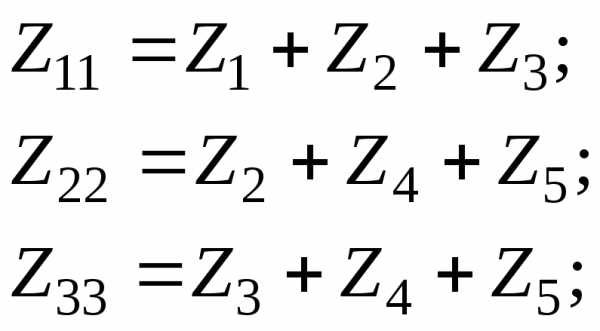
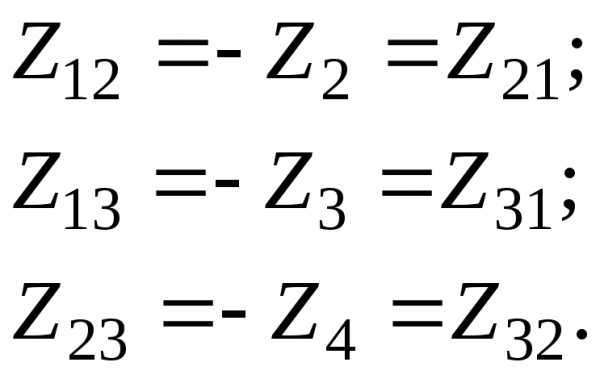
E11= E1; E22 = 0;E33 = 0.
3) По методу Крамера находим контурные токи Iki =  .
.
4) Находим токи в ветвях: I1 = Ik1; I2 = = Ik1 – Ik2; I3 = Ik1 – Ik3; I4 = –Ik2 + Ik3; I5 = Ik2; I6 = Ik3.
Пример 2. Рассмотрим электрической цепи постоянного тока, рис. 2.21.
1. Проводим топологический анализ
а) b= 5; б)y= 3;в)Nk= 5 – 3 + 1=3.
2) Для каждого контура записывают уравнение второго закона Кирхгофа,
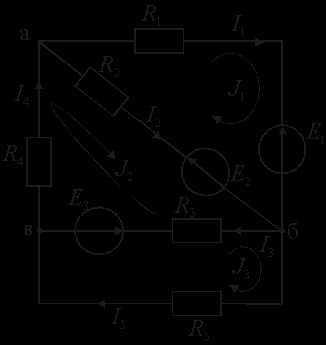 Рис. 2.21. – Расчетная схема для метода контурных токов
Рис. 2.21. – Расчетная схема для метода контурных токов
В каждом из трех контуров протекает свой контурный ток J1, J2, J3. Произвольно выбираем направление этих токов, например, по часовой стрелке. Составляем уравнения по второму закону Кирхгофа для каждого контура с учетом соседних контурных токов, протекающих по смежным ветвям
(R1 + R2)·J1 - R2·J2 = E2 - E1
- R2·J1 + (R2 + R3 + R4)·J2 - R3·J3 = - E2 - E3
- R3·J2 + (R3 + R5)·J3 = E3.
Решив систему уравнений, находят контурные токи J1, J2, J3. Затем определяют реальные токи в ветвях, причем токи во внешних ветвях равны контурным, а в смежных – алгебраической сумме 2-х контурных токов, протекающих в данной ветви
I1 = J1; I2 = J2 - J1; I3 = J2 - J3; I4 = J2; I5 = J3.
Исходная система уравнений в матричной форме
или
[R]·[J] = [E],
где [R] – квадратная матрица коэффициентов контурных токов;
[J] – матрица – столбец контурных токов; [E] – матрица – столбец ЭДС.
Решением матричного уравнения является матрица
[J] = [R]-1 ·[E],
где [R]-1 – матрица, обратная матрице [R]
Пример 3. Для электрической цепи, схема которой приведена на рис. 1.1, получим следующие уравнения:
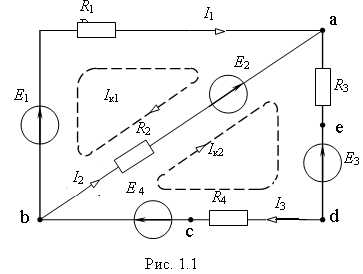
получим следующие уравнения:
По методу Крамера найдем контурные токи:
Действительные токи в ветвях: I1 = Ik1; I2 = Ik2 – Ik1; I3 = Ik2.
Пример 4. Расчет цепи методом контурных токов на рис. 2.22.
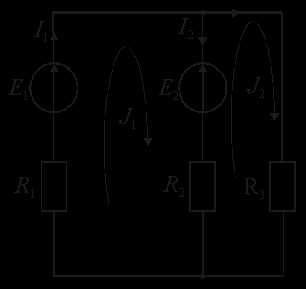 Рис. 2.22. – Расчет цепи методом контурных токов
Рис. 2.22. – Расчет цепи методом контурных токов
Для схемы замещения электрической цепи, показанной на рис. 2.22, задано: E1 = 30 B; E2 = 10 В; R1 = 8 Ом; R2 = 15 Ом; R3 = 36 Ом. Требуется определить токи в ветвях методом контурных токов. Составить баланс мощности.
Схема содержит три ветви (m = 3), два узла (n = 2). Выбираем положительные направления токов в ветвях произвольно. Число уравнений, составленных по методу контурных токов, равно m - (n - 1) = 2. Задаем направление контурных токов (например, по часовой стрелке) и составляем систему уравнений
(R1 + R2)·J1 - R2·J2 = E1 - E2
- R2·J1 + (R2 + R3)·J2 = E2.
Подставляя численные значения сопротивлений резисторов и ЭДС в приведённые уравнения, находим контурные токи J1, J2 (Например, методом определителей)
20 = 23·J1 – 15·J2
10 = - 15·J1 + 51·J2

Токи в ветвях
I1 = J1 = 1,23 А; I2 = - J2 + J1 = 1,23 - 0,56 = 0,67 А; I3 = J2 = 0,56 А.
Составляем баланс мощностей.
Мощность генераторов (источников)
РИ = Е1·I1 - Е2·I2 = 30·1,23 – 10·0,67 = 30,2 Вт,
где произведение Е2·I2 имеет знак минус (ток через источник не совпадает с ЭДС, значит источник ЭДС работает в режиме потребителя электрической энергии).
Мощность, потребляемая нагрузкой, составляет
РН = R1·I12 + R2·I22 + R3·I32 = 8·1,232 + 15·0,562 + 36·0,562 = 30,13 Вт.
Погрешность
составляет менее 1%, т. е. токи найдены верно.
Метод узловых потенциалов (МУП)
Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.
Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).
а) I = E/ZiI;
б) ZiII = ZiI.
1) Топологический анализ.
а) Подсчитывают число ветвей bи число узловy.Определяется количество независимых узловNy =y – 1.
б) Нумеруют все узлы. Один из узлов, к которому сходится наибольшее число ветвей, считают нулевым, где 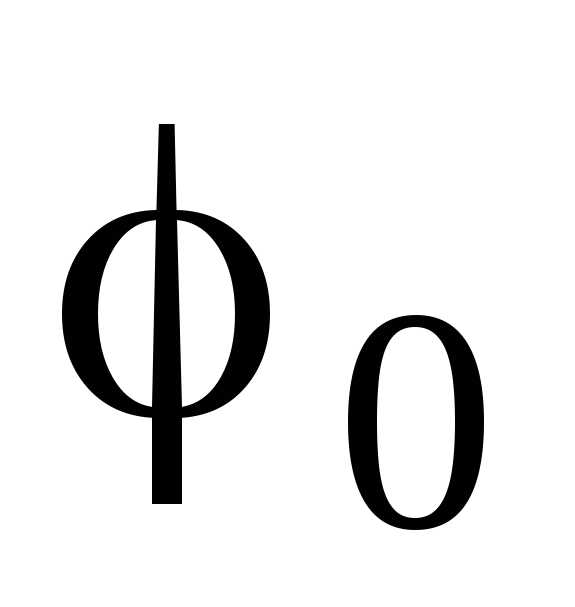 – потенциал нулевого узла.
– потенциал нулевого узла.
2) По 1-му закону Кирхгофа составляют уравнения для Nузлов схемы и решают их относительно потенциалов узлов:
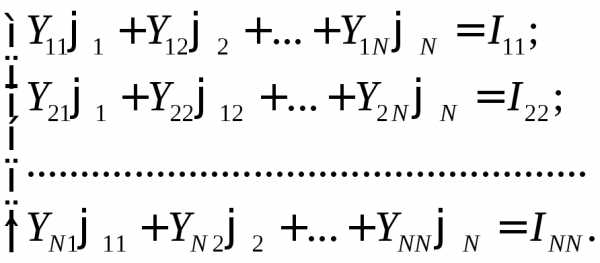 ,
,
где Yii– собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся вi-м узле, все они берутся со знаком «+»;
Yij– межузловая проводимость междуi-м иj-м узлами. Проводимости всех узлов берутся со знаком «–»;
Iii– алгебраическая сумма токов источников тока, сходящихся вi-м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».
3) Потенциалы узлов находят по формуле Крамера
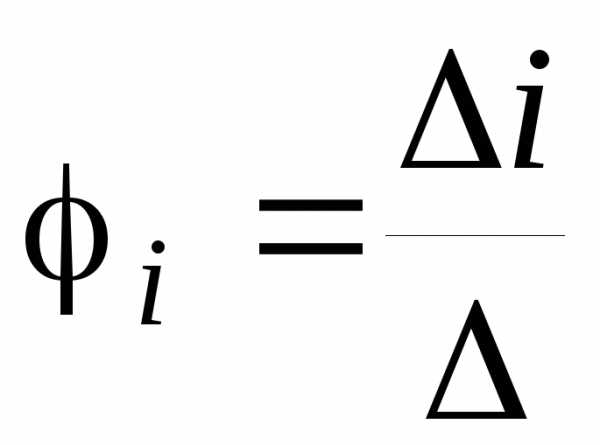 .
.
4) Токи в ветвях находят по закону Ома
I= (1 –2)/Z.
Пример.Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.
П
I2
Z2
редварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33).
Z1
Z2
Z3
Z4
E1
E2
I
I1
I2
I4
I
I3
I1
Z1
Z3
Z4
Рис. 4.32 Рис. 4.33Проведем топологический анализ.
а) число ветвей b= 4;
б) число независимых узлов Nу= 2, их потенциалы: φ1и φ2(рис. 4.33).
Составим систему уравнений по методу узловых потенциалов:
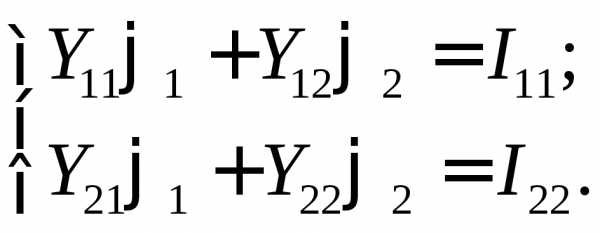
;
.
По методу Крамера найдем потенциалы узлов 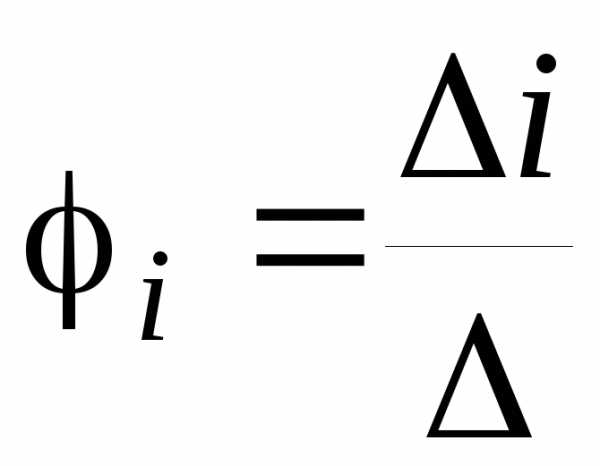 .
.
По закону Ома найдем токи во всех ветвях схемы:
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме цепи переменного тока
studfiles.net