Правило буравчика. Правило правой руки буравчика

Буравчика правило - Википедия

Материал из Википедии — свободной энциклопедии

(перенаправлено с «»)Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 апреля 2017; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 апреля 2017; проверки требует 1 правка.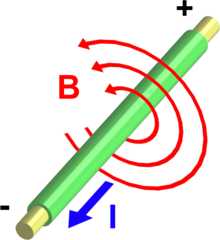 Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки, — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трёхмерном пространстве, соглашения о положительной ориентации базиса в нём, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

encyclopaedia.bid

Правило буравчика - это... Что такое Правило буравчика?

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так:

Для векторного произведения

Правило буравчика (винта) для векторного произведения: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет завинчиваться в направлении вектора-произведения.

• (Под винтом и буравчком здесь имеются в виду винт с правой резьбой, каковых абсолютное большинство в технике и что является в ней повсеместным стандартом[7], или буравчик также с правым винтом на острие, каково также абсолютное большинство реальных инструментов).
• Это можно переформулировать в терминах часовой стрелки, поскольку правый винт по определению это такой винт, который завинчивается (вперед), когда мы вращаем его по часовой стрелке.

Вариант правило буравчика (винта) для векторного произведения через часовую стрелку: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю и смотреть с той стороны, чтобы это вращение было для нас по часовой стрелке, вектор-произведение будет направлен от нас (завинчиваться вглубь часов).

Правило правой руки для векторного произведения (первый вариант):

Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения.

Правило правой руки для векторного произведения (второй вариант):

Если нарисовать векторы так, чтобы их начала совпадали и первый (большой) палец правой руки направить вдоль первого вектора-сомножителя, второй (указательный) — вдоль второго вектора-сомножителя, то третий (средний) покажет (приблизительно) направление вектора-произведения (см. рисунок).

Для базисов

Все эти правила могут быть, конечно, переписаны для определения ориентации базисов. Перепишем только два из них: Правило правой руки для базиса:

x, y,z — правая система координат.

Если в базисе (состоящем из векторов вдоль осей x, y,z) первый (большой) палец правой руки направить вдоль первого базисного вектора (то есть по оси x), второй (указательный) — вдоль второго (то есть по оси y), а третий (средний) окажется направленным (приблизительно) в направлении третьего (по z), то это правый базис (как и оказалось на рисунке).

Правило буравчика (винта) для базиса: Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис.

• Всё это, конечно, соответствует расширению обычного правила выбора направления координат на плоскости (х — вправо, у — вверх, z — на нас). Последнее может быть еще одним мнемоническим правилом, в принципе способным заменить правило буравчика, правой руки и т.д. (впрочем, пользование им, вероятно, требует иногда определенного пространственного воображения, так как надо мысленно повернуть нарисованные обычным образом координаты до совпадения их с базисом, ориентацию которого мы хотим определить, а он может быть развернут как угодно).

Формулировки правила буравчика (винта) или правила правой руки для специальных случаев

Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.

Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях[8].

Правило правой руки или буравчика (винта) для механического вращения скорости

Правило правой руки или буравчика (винта) для угловой скорости

Известно, что вектор скорости данной точки связан с вектором угловой скорости и вектором , проведенным из неподвижной точки в данную, как их векторное произведение:

Очевидно, поэтому к определению направления вектора угловой скорости применимы правило винта и правило правой руки, описанные выше для векторного произведения.

Этого в принципе достаточно.

Однако в данном случае правила могут быть сформулированы в еще более простом и запоминающемся варианте, так как речь идет о вполне реальном вращении:

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.

Правило правой руки: Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.

Правило правой руки или буравчика (винта) для момента импульса

Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом[9].

Правило правой руки или буравчика (винта) для момента сил

Для момента сил (вращающего момента)

(где  — сила, приложенная к i-ой точке тела,  — радиус-вектор,  — знак векторного умножения),

правила тоже в целом аналогичны, однако сформулируем их явно.

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Правило правой руки и буравчика (винта) в магнитостатике и электродинамике

Для магнитной индукции (закона Био - Савара)

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

Правило правой руки

Правило правой руки: Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции, поля, создаваемого этим током и огибающих проводник, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

Для соленоида оно формулируется так: Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Наука не в состоянии объяснить, почему вокруг проводника с током, как экспериментально установлено, вектор магнитной индукции направлен вправо, а не влево, или спонтанно в каждом конкретном случае.

Для тока в проводнике, движущемся в магнитном поле

Правило правой руки: Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Для уравнений Максвелла

Поскольку операция ротор (обозначаемая rot), используемая в двух уравнениях Максвелла, может быть записана формально как векторное произведение (с оператором набла), а главное потому, что ротор векторного поля может быть уподоблен (представляет собой аналогию) угловой скорости[10] вращения жидкости, поле скоростей течения которой изображает собой данное векторное поле, можно воспользоваться для ротора теми формулировками правила, которые уже описаны выше для угловой скорости.

Таким образом, если крутить буравчик в направлении завихрения векторного поля, то он будет ввинчиваться в направлении вектора ротора этого поля.

Или: если направить четыре пальца правой руки, сжатой в кулак, в направлении завихрения, то отогнутый большой палец покажет направление ротора.

Из этого следуют правила для закона электромагнитной индукции, например: если указать отогнутым большим пальцем правой руки направление магнитного потока через контур, если он растет, и противоположное направление, если он убывает, то согнутые пальцы, охватывающие контур, покажут направление, противоположное (из-за знака минус в формуле) направлению ЭДС в этом контуре, индуцируемой меняющимся магнитным потоком.

Правила для закона Ампера - Максвелла в целом совпадают с правилами, приведенными выше для вектора магнитной индукции, создаваемой током, только в данном случае надо добавить к электрическому току через контур поток быстроты изменения электрического поля через этот контур и говорить о магнитном поле можно в терминах его циркуляции по контуру.

Правила левой руки

Первое правило левой руки

Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.

Второе правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».

Примечания

1. ↑ Математические детали общего понятия ориентации базиса, о котором здесь идет речь — см. в статье Ориентация.
2. ↑ Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
3. ↑ Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
4. ↑ Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
5. ↑ Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
6. ↑ Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведенное здесь определение, указано там.
7. ↑ Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса. Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
8. ↑ В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более легким, чем запоминание всего одного общего правила.
9. ↑ Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
10. ↑ Строго говоря, при этом сопоставлении есть еще постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

См. также

Cсылки

dal.academic.ru

Правило буравчика - это... Что такое Правило буравчика?

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так:

Для векторного произведения

Правило буравчика (винта) для векторного произведения: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет завинчиваться в направлении вектора-произведения.

• (Под винтом и буравчком здесь имеются в виду винт с правой резьбой, каковых абсолютное большинство в технике и что является в ней повсеместным стандартом[7], или буравчик также с правым винтом на острие, каково также абсолютное большинство реальных инструментов).
• Это можно переформулировать в терминах часовой стрелки, поскольку правый винт по определению это такой винт, который завинчивается (вперед), когда мы вращаем его по часовой стрелке.

Вариант правило буравчика (винта) для векторного произведения через часовую стрелку: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю и смотреть с той стороны, чтобы это вращение было для нас по часовой стрелке, вектор-произведение будет направлен от нас (завинчиваться вглубь часов).

Правило правой руки для векторного произведения (первый вариант):

Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения.

Правило правой руки для векторного произведения (второй вариант):

Если нарисовать векторы так, чтобы их начала совпадали и первый (большой) палец правой руки направить вдоль первого вектора-сомножителя, второй (указательный) — вдоль второго вектора-сомножителя, то третий (средний) покажет (приблизительно) направление вектора-произведения (см. рисунок).

Для базисов

Все эти правила могут быть, конечно, переписаны для определения ориентации базисов. Перепишем только два из них: Правило правой руки для базиса:

x, y,z — правая система координат.

Если в базисе (состоящем из векторов вдоль осей x, y,z) первый (большой) палец правой руки направить вдоль первого базисного вектора (то есть по оси x), второй (указательный) — вдоль второго (то есть по оси y), а третий (средний) окажется направленным (приблизительно) в направлении третьего (по z), то это правый базис (как и оказалось на рисунке).

Правило буравчика (винта) для базиса: Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис.

• Всё это, конечно, соответствует расширению обычного правила выбора направления координат на плоскости (х — вправо, у — вверх, z — на нас). Последнее может быть еще одним мнемоническим правилом, в принципе способным заменить правило буравчика, правой руки и т.д. (впрочем, пользование им, вероятно, требует иногда определенного пространственного воображения, так как надо мысленно повернуть нарисованные обычным образом координаты до совпадения их с базисом, ориентацию которого мы хотим определить, а он может быть развернут как угодно).

Формулировки правила буравчика (винта) или правила правой руки для специальных случаев

Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.

Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях[8].

Правило правой руки или буравчика (винта) для механического вращения скорости

Правило правой руки или буравчика (винта) для угловой скорости

Известно, что вектор скорости данной точки связан с вектором угловой скорости и вектором , проведенным из неподвижной точки в данную, как их векторное произведение:

Очевидно, поэтому к определению направления вектора угловой скорости применимы правило винта и правило правой руки, описанные выше для векторного произведения.

Этого в принципе достаточно.

Однако в данном случае правила могут быть сформулированы в еще более простом и запоминающемся варианте, так как речь идет о вполне реальном вращении:

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.

Правило правой руки: Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.

Правило правой руки или буравчика (винта) для момента импульса

Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом[9].

Правило правой руки или буравчика (винта) для момента сил

Для момента сил (вращающего момента)

(где  — сила, приложенная к i-ой точке тела,  — радиус-вектор,  — знак векторного умножения),

правила тоже в целом аналогичны, однако сформулируем их явно.

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Правило правой руки и буравчика (винта) в магнитостатике и электродинамике

Для магнитной индукции (закона Био - Савара)

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

Правило правой руки

Правило правой руки: Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции, поля, создаваемого этим током и огибающих проводник, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

Для соленоида оно формулируется так: Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Наука не в состоянии объяснить, почему вокруг проводника с током, как экспериментально установлено, вектор магнитной индукции направлен вправо, а не влево, или спонтанно в каждом конкретном случае.

Для тока в проводнике, движущемся в магнитном поле

Правило правой руки: Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Для уравнений Максвелла

Поскольку операция ротор (обозначаемая rot), используемая в двух уравнениях Максвелла, может быть записана формально как векторное произведение (с оператором набла), а главное потому, что ротор векторного поля может быть уподоблен (представляет собой аналогию) угловой скорости[10] вращения жидкости, поле скоростей течения которой изображает собой данное векторное поле, можно воспользоваться для ротора теми формулировками правила, которые уже описаны выше для угловой скорости.

Таким образом, если крутить буравчик в направлении завихрения векторного поля, то он будет ввинчиваться в направлении вектора ротора этого поля.

Или: если направить четыре пальца правой руки, сжатой в кулак, в направлении завихрения, то отогнутый большой палец покажет направление ротора.

Из этого следуют правила для закона электромагнитной индукции, например: если указать отогнутым большим пальцем правой руки направление магнитного потока через контур, если он растет, и противоположное направление, если он убывает, то согнутые пальцы, охватывающие контур, покажут направление, противоположное (из-за знака минус в формуле) направлению ЭДС в этом контуре, индуцируемой меняющимся магнитным потоком.

Правила для закона Ампера - Максвелла в целом совпадают с правилами, приведенными выше для вектора магнитной индукции, создаваемой током, только в данном случае надо добавить к электрическому току через контур поток быстроты изменения электрического поля через этот контур и говорить о магнитном поле можно в терминах его циркуляции по контуру.

Правила левой руки

Первое правило левой руки

Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.

Второе правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».

Примечания

1. ↑ Математические детали общего понятия ориентации базиса, о котором здесь идет речь — см. в статье Ориентация.
2. ↑ Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
3. ↑ Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
4. ↑ Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
5. ↑ Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
6. ↑ Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведенное здесь определение, указано там.
7. ↑ Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса. Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
8. ↑ В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более легким, чем запоминание всего одного общего правила.
9. ↑ Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
10. ↑ Строго говоря, при этом сопоставлении есть еще постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

См. также

Cсылки

biograf.academic.ru

Правило буравчика - это... Что такое Правило буравчика?

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так:

Для векторного произведения

Правило буравчика (винта) для векторного произведения: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет завинчиваться в направлении вектора-произведения.

• (Под винтом и буравчком здесь имеются в виду винт с правой резьбой, каковых абсолютное большинство в технике и что является в ней повсеместным стандартом[7], или буравчик также с правым винтом на острие, каково также абсолютное большинство реальных инструментов).
• Это можно переформулировать в терминах часовой стрелки, поскольку правый винт по определению это такой винт, который завинчивается (вперед), когда мы вращаем его по часовой стрелке.

Вариант правило буравчика (винта) для векторного произведения через часовую стрелку: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю и смотреть с той стороны, чтобы это вращение было для нас по часовой стрелке, вектор-произведение будет направлен от нас (завинчиваться вглубь часов).

Правило правой руки для векторного произведения (первый вариант):

Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения.

Правило правой руки для векторного произведения (второй вариант):

Если нарисовать векторы так, чтобы их начала совпадали и первый (большой) палец правой руки направить вдоль первого вектора-сомножителя, второй (указательный) — вдоль второго вектора-сомножителя, то третий (средний) покажет (приблизительно) направление вектора-произведения (см. рисунок).

Для базисов

Все эти правила могут быть, конечно, переписаны для определения ориентации базисов. Перепишем только два из них: Правило правой руки для базиса:

x, y,z — правая система координат.

Если в базисе (состоящем из векторов вдоль осей x, y,z) первый (большой) палец правой руки направить вдоль первого базисного вектора (то есть по оси x), второй (указательный) — вдоль второго (то есть по оси y), а третий (средний) окажется направленным (приблизительно) в направлении третьего (по z), то это правый базис (как и оказалось на рисунке).

Правило буравчика (винта) для базиса: Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис.

• Всё это, конечно, соответствует расширению обычного правила выбора направления координат на плоскости (х — вправо, у — вверх, z — на нас). Последнее может быть еще одним мнемоническим правилом, в принципе способным заменить правило буравчика, правой руки и т.д. (впрочем, пользование им, вероятно, требует иногда определенного пространственного воображения, так как надо мысленно повернуть нарисованные обычным образом координаты до совпадения их с базисом, ориентацию которого мы хотим определить, а он может быть развернут как угодно).

Формулировки правила буравчика (винта) или правила правой руки для специальных случаев

Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.

Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях[8].

Правило правой руки или буравчика (винта) для механического вращения скорости

Правило правой руки или буравчика (винта) для угловой скорости

Известно, что вектор скорости данной точки связан с вектором угловой скорости и вектором , проведенным из неподвижной точки в данную, как их векторное произведение:

Очевидно, поэтому к определению направления вектора угловой скорости применимы правило винта и правило правой руки, описанные выше для векторного произведения.

Этого в принципе достаточно.

Однако в данном случае правила могут быть сформулированы в еще более простом и запоминающемся варианте, так как речь идет о вполне реальном вращении:

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.

Правило правой руки: Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.

Правило правой руки или буравчика (винта) для момента импульса

Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом[9].

Правило правой руки или буравчика (винта) для момента сил

Для момента сил (вращающего момента)

(где  — сила, приложенная к i-ой точке тела,  — радиус-вектор,  — знак векторного умножения),

правила тоже в целом аналогичны, однако сформулируем их явно.

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Правило правой руки и буравчика (винта) в магнитостатике и электродинамике

Для магнитной индукции (закона Био - Савара)

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

Правило правой руки

Правило правой руки: Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции, поля, создаваемого этим током и огибающих проводник, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

Для соленоида оно формулируется так: Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Наука не в состоянии объяснить, почему вокруг проводника с током, как экспериментально установлено, вектор магнитной индукции направлен вправо, а не влево, или спонтанно в каждом конкретном случае.

Для тока в проводнике, движущемся в магнитном поле

Правило правой руки: Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Для уравнений Максвелла

Поскольку операция ротор (обозначаемая rot), используемая в двух уравнениях Максвелла, может быть записана формально как векторное произведение (с оператором набла), а главное потому, что ротор векторного поля может быть уподоблен (представляет собой аналогию) угловой скорости[10] вращения жидкости, поле скоростей течения которой изображает собой данное векторное поле, можно воспользоваться для ротора теми формулировками правила, которые уже описаны выше для угловой скорости.

Таким образом, если крутить буравчик в направлении завихрения векторного поля, то он будет ввинчиваться в направлении вектора ротора этого поля.

Или: если направить четыре пальца правой руки, сжатой в кулак, в направлении завихрения, то отогнутый большой палец покажет направление ротора.

Из этого следуют правила для закона электромагнитной индукции, например: если указать отогнутым большим пальцем правой руки направление магнитного потока через контур, если он растет, и противоположное направление, если он убывает, то согнутые пальцы, охватывающие контур, покажут направление, противоположное (из-за знака минус в формуле) направлению ЭДС в этом контуре, индуцируемой меняющимся магнитным потоком.

Правила для закона Ампера - Максвелла в целом совпадают с правилами, приведенными выше для вектора магнитной индукции, создаваемой током, только в данном случае надо добавить к электрическому току через контур поток быстроты изменения электрического поля через этот контур и говорить о магнитном поле можно в терминах его циркуляции по контуру.

Правила левой руки

Первое правило левой руки

Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.

Второе правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».

Примечания

1. ↑ Математические детали общего понятия ориентации базиса, о котором здесь идет речь — см. в статье Ориентация.
2. ↑ Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
3. ↑ Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
4. ↑ Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
5. ↑ Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
6. ↑ Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведенное здесь определение, указано там.
7. ↑ Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса. Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
8. ↑ В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более легким, чем запоминание всего одного общего правила.
9. ↑ Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
10. ↑ Строго говоря, при этом сопоставлении есть еще постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

См. также

Cсылки

dikc.academic.ru

Правило буравчика - это... Что такое Правило буравчика?

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так:

Для векторного произведения

Правило буравчика (винта) для векторного произведения: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет завинчиваться в направлении вектора-произведения.

• (Под винтом и буравчком здесь имеются в виду винт с правой резьбой, каковых абсолютное большинство в технике и что является в ней повсеместным стандартом[7], или буравчик также с правым винтом на острие, каково также абсолютное большинство реальных инструментов).
• Это можно переформулировать в терминах часовой стрелки, поскольку правый винт по определению это такой винт, который завинчивается (вперед), когда мы вращаем его по часовой стрелке.

Вариант правило буравчика (винта) для векторного произведения через часовую стрелку: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю и смотреть с той стороны, чтобы это вращение было для нас по часовой стрелке, вектор-произведение будет направлен от нас (завинчиваться вглубь часов).

Правило правой руки для векторного произведения (первый вариант):

Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения.

Правило правой руки для векторного произведения (второй вариант):

Если нарисовать векторы так, чтобы их начала совпадали и первый (большой) палец правой руки направить вдоль первого вектора-сомножителя, второй (указательный) — вдоль второго вектора-сомножителя, то третий (средний) покажет (приблизительно) направление вектора-произведения (см. рисунок).

Для базисов

Все эти правила могут быть, конечно, переписаны для определения ориентации базисов. Перепишем только два из них: Правило правой руки для базиса:

x, y,z — правая система координат.

Если в базисе (состоящем из векторов вдоль осей x, y,z) первый (большой) палец правой руки направить вдоль первого базисного вектора (то есть по оси x), второй (указательный) — вдоль второго (то есть по оси y), а третий (средний) окажется направленным (приблизительно) в направлении третьего (по z), то это правый базис (как и оказалось на рисунке).

Правило буравчика (винта) для базиса: Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис.

• Всё это, конечно, соответствует расширению обычного правила выбора направления координат на плоскости (х — вправо, у — вверх, z — на нас). Последнее может быть еще одним мнемоническим правилом, в принципе способным заменить правило буравчика, правой руки и т.д. (впрочем, пользование им, вероятно, требует иногда определенного пространственного воображения, так как надо мысленно повернуть нарисованные обычным образом координаты до совпадения их с базисом, ориентацию которого мы хотим определить, а он может быть развернут как угодно).

Формулировки правила буравчика (винта) или правила правой руки для специальных случаев

Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.

Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях[8].

Правило правой руки или буравчика (винта) для механического вращения скорости

Правило правой руки или буравчика (винта) для угловой скорости

Известно, что вектор скорости данной точки связан с вектором угловой скорости и вектором , проведенным из неподвижной точки в данную, как их векторное произведение:

Очевидно, поэтому к определению направления вектора угловой скорости применимы правило винта и правило правой руки, описанные выше для векторного произведения.

Этого в принципе достаточно.

Однако в данном случае правила могут быть сформулированы в еще более простом и запоминающемся варианте, так как речь идет о вполне реальном вращении:

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.

Правило правой руки: Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.

Правило правой руки или буравчика (винта) для момента импульса

Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом[9].

Правило правой руки или буравчика (винта) для момента сил

Для момента сил (вращающего момента)

(где  — сила, приложенная к i-ой точке тела,  — радиус-вектор,  — знак векторного умножения),

правила тоже в целом аналогичны, однако сформулируем их явно.

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Правило правой руки и буравчика (винта) в магнитостатике и электродинамике

Для магнитной индукции (закона Био - Савара)

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

Правило правой руки

Правило правой руки: Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции, поля, создаваемого этим током и огибающих проводник, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

Для соленоида оно формулируется так: Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Наука не в состоянии объяснить, почему вокруг проводника с током, как экспериментально установлено, вектор магнитной индукции направлен вправо, а не влево, или спонтанно в каждом конкретном случае.

Для тока в проводнике, движущемся в магнитном поле

Правило правой руки: Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Для уравнений Максвелла

Поскольку операция ротор (обозначаемая rot), используемая в двух уравнениях Максвелла, может быть записана формально как векторное произведение (с оператором набла), а главное потому, что ротор векторного поля может быть уподоблен (представляет собой аналогию) угловой скорости[10] вращения жидкости, поле скоростей течения которой изображает собой данное векторное поле, можно воспользоваться для ротора теми формулировками правила, которые уже описаны выше для угловой скорости.

Таким образом, если крутить буравчик в направлении завихрения векторного поля, то он будет ввинчиваться в направлении вектора ротора этого поля.

Или: если направить четыре пальца правой руки, сжатой в кулак, в направлении завихрения, то отогнутый большой палец покажет направление ротора.

Из этого следуют правила для закона электромагнитной индукции, например: если указать отогнутым большим пальцем правой руки направление магнитного потока через контур, если он растет, и противоположное направление, если он убывает, то согнутые пальцы, охватывающие контур, покажут направление, противоположное (из-за знака минус в формуле) направлению ЭДС в этом контуре, индуцируемой меняющимся магнитным потоком.

Правила для закона Ампера - Максвелла в целом совпадают с правилами, приведенными выше для вектора магнитной индукции, создаваемой током, только в данном случае надо добавить к электрическому току через контур поток быстроты изменения электрического поля через этот контур и говорить о магнитном поле можно в терминах его циркуляции по контуру.

Правила левой руки

Первое правило левой руки

Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.

Второе правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».

Примечания

1. ↑ Математические детали общего понятия ориентации базиса, о котором здесь идет речь — см. в статье Ориентация.
2. ↑ Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
3. ↑ Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
4. ↑ Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
5. ↑ Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
6. ↑ Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведенное здесь определение, указано там.
7. ↑ Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса. Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
8. ↑ В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более легким, чем запоминание всего одного общего правила.
9. ↑ Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
10. ↑ Строго говоря, при этом сопоставлении есть еще постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

См. также

Cсылки

dvc.academic.ru

Правило буравчика - это... Что такое Правило буравчика?

Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трехмерном пространстве, соглашения о положительной ориентации базиса в нем, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

Общее (главное) правило

Главным правилом - которое может использоваться и в варианте правила буравчика (винта) и в варианте правила правой руки - это правило выбора направления для базисов и векторного произведения (или даже для чего-то одного из двух, т.к. одно прямо определяется через другое). Главным оно является потому, что в принципе его достаточно для использования во всех случаях вместо всех остальных правил, если только знать порядок сомножителей в соответствующих формулах.

Выбор правила для определения положительного направления векторного произведения и для положительного базиса (системы координат) в трехмерном пространстве — тесно взаимосвязаны.

Левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято считать положительным и использовать по умолчанию правый (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно).

Оба эти правила в принципе чисто условны[4], однако принято (по крайней мере, если обратное явно не оговорено) считать, и это общепринятое соглашение, что положительным является правый базис, а векторное произведение определяется так, что для положительного ортонормированного[5] базиса (базиса прямоугольных декартовых координат с единичным масштабом по всем осям, состоящего из единичных векторов по всем осям) выполняется[6] следующее:

где косым крестом обозначена операция векторного умножения.

По умолчанию же общепринято использовать положительные (и таким образом правые) базисы. Левые базисы в принципе принято использовать в основном когда использовать правый очень неудобно или вообще невозможно (например, если у нас правый базис отражается в зеркале, то отражение представляет собой левый базис, и с этим ничего не поделаешь).

Поэтому правило для векторного произведения и правило для выбора (постороения) положительного базиса взаимно согласованы.

Они могут быть сформулированы так:

Для векторного произведения

Правило буравчика (винта) для векторного произведения: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет завинчиваться в направлении вектора-произведения.

• (Под винтом и буравчком здесь имеются в виду винт с правой резьбой, каковых абсолютное большинство в технике и что является в ней повсеместным стандартом[7], или буравчик также с правым винтом на острие, каково также абсолютное большинство реальных инструментов).
• Это можно переформулировать в терминах часовой стрелки, поскольку правый винт по определению это такой винт, который завинчивается (вперед), когда мы вращаем его по часовой стрелке.

Вариант правило буравчика (винта) для векторного произведения через часовую стрелку: Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю и смотреть с той стороны, чтобы это вращение было для нас по часовой стрелке, вектор-произведение будет направлен от нас (завинчиваться вглубь часов).

Правило правой руки для векторного произведения (первый вариант):

Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения.

Правило правой руки для векторного произведения (второй вариант):

Если нарисовать векторы так, чтобы их начала совпадали и первый (большой) палец правой руки направить вдоль первого вектора-сомножителя, второй (указательный) — вдоль второго вектора-сомножителя, то третий (средний) покажет (приблизительно) направление вектора-произведения (см. рисунок).

Для базисов

Все эти правила могут быть, конечно, переписаны для определения ориентации базисов. Перепишем только два из них: Правило правой руки для базиса:

x, y,z — правая система координат.

Если в базисе (состоящем из векторов вдоль осей x, y,z) первый (большой) палец правой руки направить вдоль первого базисного вектора (то есть по оси x), второй (указательный) — вдоль второго (то есть по оси y), а третий (средний) окажется направленным (приблизительно) в направлении третьего (по z), то это правый базис (как и оказалось на рисунке).

Правило буравчика (винта) для базиса: Если вращать буравчик и векторы так, чтобы первый базисный вектор кратчайшим образом стремился ко второму, то буравчик (винт) будет завинчиваться в направлении третьего базисного вектора, если это правый базис.

• Всё это, конечно, соответствует расширению обычного правила выбора направления координат на плоскости (х — вправо, у — вверх, z — на нас). Последнее может быть еще одним мнемоническим правилом, в принципе способным заменить правило буравчика, правой руки и т.д. (впрочем, пользование им, вероятно, требует иногда определенного пространственного воображения, так как надо мысленно повернуть нарисованные обычным образом координаты до совпадения их с базисом, ориентацию которого мы хотим определить, а он может быть развернут как угодно).

Формулировки правила буравчика (винта) или правила правой руки для специальных случаев

Выше упоминалось о том, что все разнообразные формулировки правила буравчика (винта) или правила правой руки (и другие подобные правила), в том числе все упоминаемые ниже, не являются необходимыми. Их не обязательно знать, если знаешь (хотя бы в каком-то одном из вариантов) общее правило, описанное выше и знаешь порядок сомножителей в формулах, содержащих векторное произведение.

Однако многие из описанных ниже правил хорошо приспособлены к специальным случаям их применения и поэтому могут быть весьма удобны и легки для быстрого определения направления векторов в этих случаях[8].

Правило правой руки или буравчика (винта) для механического вращения скорости

Правило правой руки или буравчика (винта) для угловой скорости

Известно, что вектор скорости данной точки связан с вектором угловой скорости и вектором , проведенным из неподвижной точки в данную, как их векторное произведение:

Очевидно, поэтому к определению направления вектора угловой скорости применимы правило винта и правило правой руки, описанные выше для векторного произведения.

Этого в принципе достаточно.

Однако в данном случае правила могут быть сформулированы в еще более простом и запоминающемся варианте, так как речь идет о вполне реальном вращении:

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором вращается тело, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.

Правило правой руки: Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении.

Правило правой руки или буравчика (винта) для момента импульса

Полностью аналогичны правила для определения направления момента импульса, что неудивительно, поскольку момент импульса пропорционален угловой скорости с положительным коэффициентом[9].

Правило правой руки или буравчика (винта) для момента сил

Для момента сил (вращающего момента)

(где  — сила, приложенная к i-ой точке тела,  — радиус-вектор,  — знак векторного умножения),

правила тоже в целом аналогичны, однако сформулируем их явно.

Правило буравчика (винта): Если вращать винт (буравчик) в том направлении, в котором силы стремятся повернуть тело, винт будет завинчиваться (или вывинчиваться) в ту сторону, куда направлен момент этих сил.

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Правило правой руки и буравчика (винта) в магнитостатике и электродинамике

Для магнитной индукции (закона Био - Савара)

Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.

Правило правой руки

Правило правой руки: Если обхватить проводник правой рукой так, чтобы оттопыренный большой палец указывал направление тока, то остальные пальцы покажут направление огибающих проводник линий магнитной индукции, поля, создаваемого этим током и огибающих проводник, а значит и направление вектора магнитной индукции, направленного везде по касательной к этим линиям.

Для соленоида оно формулируется так: Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Наука не в состоянии объяснить, почему вокруг проводника с током, как экспериментально установлено, вектор магнитной индукции направлен вправо, а не влево, или спонтанно в каждом конкретном случае.

Для тока в проводнике, движущемся в магнитном поле

Правило правой руки: Если ладонь правой руки расположить так, чтобы в нее входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.

Для уравнений Максвелла

Поскольку операция ротор (обозначаемая rot), используемая в двух уравнениях Максвелла, может быть записана формально как векторное произведение (с оператором набла), а главное потому, что ротор векторного поля может быть уподоблен (представляет собой аналогию) угловой скорости[10] вращения жидкости, поле скоростей течения которой изображает собой данное векторное поле, можно воспользоваться для ротора теми формулировками правила, которые уже описаны выше для угловой скорости.

Таким образом, если крутить буравчик в направлении завихрения векторного поля, то он будет ввинчиваться в направлении вектора ротора этого поля.

Или: если направить четыре пальца правой руки, сжатой в кулак, в направлении завихрения, то отогнутый большой палец покажет направление ротора.

Из этого следуют правила для закона электромагнитной индукции, например: если указать отогнутым большим пальцем правой руки направление магнитного потока через контур, если он растет, и противоположное направление, если он убывает, то согнутые пальцы, охватывающие контур, покажут направление, противоположное (из-за знака минус в формуле) направлению ЭДС в этом контуре, индуцируемой меняющимся магнитным потоком.

Правила для закона Ампера - Максвелла в целом совпадают с правилами, приведенными выше для вектора магнитной индукции, создаваемой током, только в данном случае надо добавить к электрическому току через контур поток быстроты изменения электрического поля через этот контур и говорить о магнитном поле можно в терминах его циркуляции по контуру.

Правила левой руки

Первое правило левой руки

Если расположить ладонь левой руки так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно к ней, а четыре пальца направлены по току, то отставленный на 90° большой палец укажет направление силы, действующей на проводник.

Второе правило левой руки

Если движется заряд, а магнит покоится, то для определения силы действует правило левой руки: «Если левую руку расположить так, чтобы линии индукции магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по току (по движению положительно заряженной частицы или против движения отрицательно заряженной), то отставленный на 90° большой палец покажет направление действующей силы Лоренца или Ампера».

Примечания

1. ↑ Математические детали общего понятия ориентации базиса, о котором здесь идет речь — см. в статье Ориентация.
2. ↑ Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
3. ↑ Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
4. ↑ Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
5. ↑ Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
6. ↑ Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведенное здесь определение, указано там.
7. ↑ Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса. Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
8. ↑ В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более легким, чем запоминание всего одного общего правила.
9. ↑ Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
10. ↑ Строго говоря, при этом сопоставлении есть еще постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

См. также

Cсылки

3dic.academic.ru

Правило правой руки - Википедия

Материал из Википедии — свободной энциклопедии

(перенаправлено с «»)Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 апреля 2017; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 апреля 2017; проверки требует 1 правка. Прямой провод с током. Ток (I), протекая через провод, создаёт магнитное поле (B) вокруг провода.

Пра́вило бура́вчика (пра́вило винта́), или пра́вило правой руки, — варианты мнемонического правила для определения направления векторного произведения и тесно связанного с этим выбора правого базиса[1] в трёхмерном пространстве, соглашения о положительной ориентации базиса в нём, и соответственно — знака любого аксиального вектора, определяемого через ориентацию базиса.

В частности, это относится к определению направления[2] таких важных в физике аксиальных векторов, как вектор угловой скорости, характеризующий скорость вращения тела, вектор магнитной индукции B и многих других, а также для определения направления таких векторов, которые определяются через аксиальные, например, направление индукционного тока при заданном векторе магнитной индукции.

• Для многих из этих случаев кроме общей формулировки, позволяющей определять направление векторного произведения или ориентацию базиса вообще, имеются специальные формулировки правила, особенно хорошо приспособленные к каждой конкретной ситуации (но гораздо менее общие).

В принципе, как правило, выбор одного из двух возможных направлений аксиального вектора считается чисто условным, однако он должен происходить всегда одинаково, чтобы в конечном результате вычислений не оказался перепутан знак. Для этого и служат правила, составляющие предмет этой статьи (они позволяют всегда придерживаться одного и того же выбора).

• Под названием правила правой руки существует несколько достаточно различающихся правил.
• Существует также несколько вариантов правила левой руки.
• В принципе можно ограничиться выбором из всего набора этих правил в разных формулировках (или из им подобных) какого-то одного, относящегося к универсальному типу (определению знака векторного произведения или ориентации базиса). Это минимально необходимый выбор (хотя бы один вариант правила нужен: без него вообще не только в принципе невозможно следовать общепринятым соглашениям, но и крайне трудно быть последовательным даже в собственных вычислениях). Но в принципе этого и достаточно: вместо всех правил, упоминаемых в этой статье или других им подобных в принципе[3]можно пользоваться всего одним, если только знать порядок сомножителей в формулах, содержащих векторные произведения.

encyclopaedia.bid

---

• 
  Лучший шуруповерт 2018
• 
  Оптоволоконный светильник
• 
  Аэрогрили отзывы какой лучше
• 
  Для чего уф лампа
• 
  Электрический котел расход электроэнергии
• 
  Где производят стиральные машины
• 
  Лампочка энергосберегающая моргает
• 
  Применение самоиндукция
• 
  Неисправности микроволновых печей
• 
  Телефонные розетки rj 11
• 
  Как восстановить пальчиковые батарейки