ул.Симферопольская
дом 5, офис 9
![]() Корзина
Корзина
Корзина пуста
Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца. Объясните зависимость сопротивления металла от температуры
Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
(14.11)
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.ρ=ρ0(1+αt) (14.12)
где ρ0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α <0.
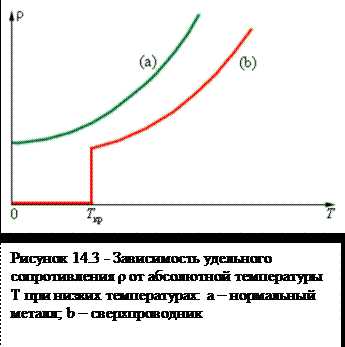 На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега <ℓ>, т.е. чем больше <ℓ>, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости <υτ>. Тепловая скорость при повышении температуры возрастает пропорционально , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега <ℓ>, т.е. чем больше <ℓ>, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости <υτ>. Тепловая скорость при повышении температуры возрастает пропорционально , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью. В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н.Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
(14.13)
(n – концентрация атомов, m -масса атома, <ℓ> -средняя длина свободного пробега электрона, cV-удельная теплоёмкость).
Для одноатомного газа
(k -постоянная Больцмана, М –молярная масса).
Тогда
(14.14)
Из уравнений (14.7) и (14.14) находим отношение теплопроводности и электропроводности металла:
(14.15)
Из кинетической теории газов известно, что , тогда
(14.16)
( k и е – постоянные величины).
Поэтому отношение теплопроводности и электропроводности металла пропорционально термодинамической температуре, что и было установлено законом Видемана-Франца. Так как k =1,38∙10-23Дж/К; е = 1,6∙10-19Кл, то
(14.17)
Закон Видемана-Франца для большинства металлов выполняется при температуре 100-400 К, но при низкой температуре закон существенно нарушается. Имеются металлы (бериллий, марганец) которые совсем не подчиняются закону Видемана-Франца. Выход из непреодолимых противоречий был найден в квантовой электронной теории металлов.
Похожие статьи:
poznayka.org
Закон Джоуля-Ленца в классической электронной теории
На основании классической электронной теории проводимости металлов можно объяснить закон Джоуля-Ленца.
Упорядоченное движение электронов происходит под действием сил поля. Как и выше, будем считать, что в момент соударения с положительными ионами кристаллической решётки электроны полностью передают ей свою кинетическую энергию. К концу свободного пробега скорость электрона 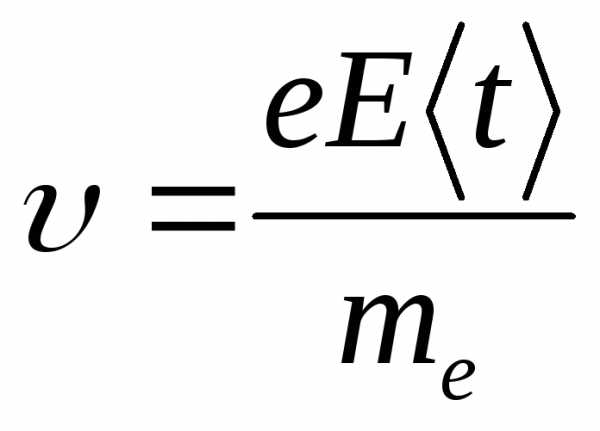
(14.9)
Мощность, выделяемая единицей объёма металла (плотность мощности), равна произведению энергии одного электрона на число соударений в секунду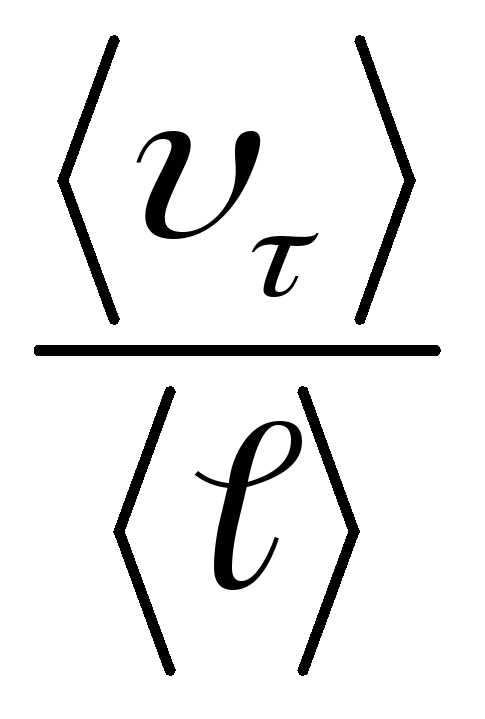 и на концентрациюn электронов:
и на концентрациюn электронов:
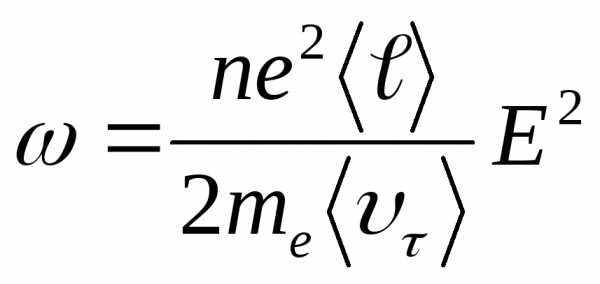 (14.10)
(14.10)
Учитывая (14.7), имеем
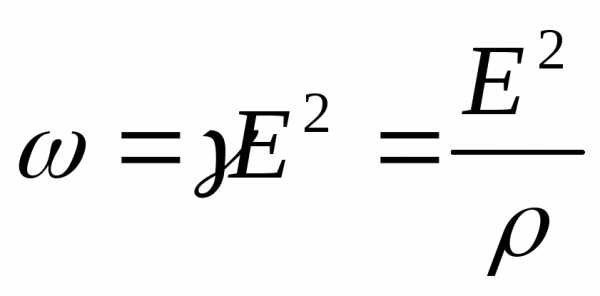
- закон Джоуля-Ленца в дифференциальной форме.
Если нас интересует энергия, выделяемая проводником длиной ℓ, площадью поперечного сечения S за промежуток времени dt, то выражение (14.10) нужно умножить на объём проводника V=St и время dt:
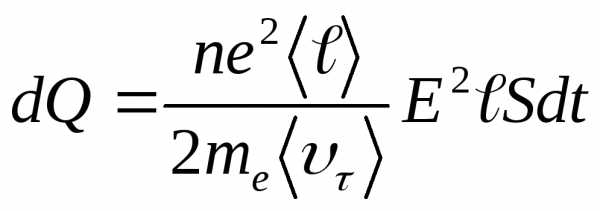
Учитывая, что 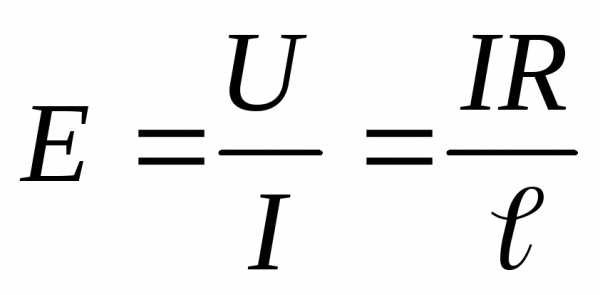
§ 14.3 Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
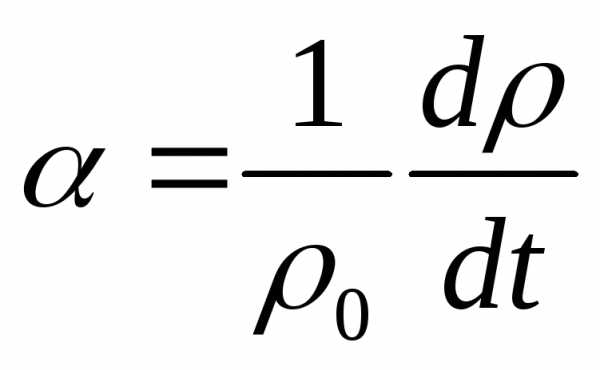 (14.11)
(14.11)
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Рисунок 14.3
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.ρ=ρ0(1+αt) (14.12)
где ρ0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α <0.
На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега <ℓ>, т.е. чем больше <ℓ>, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости <υτ>. Тепловая скорость при повышении температуры возрастает пропорционально 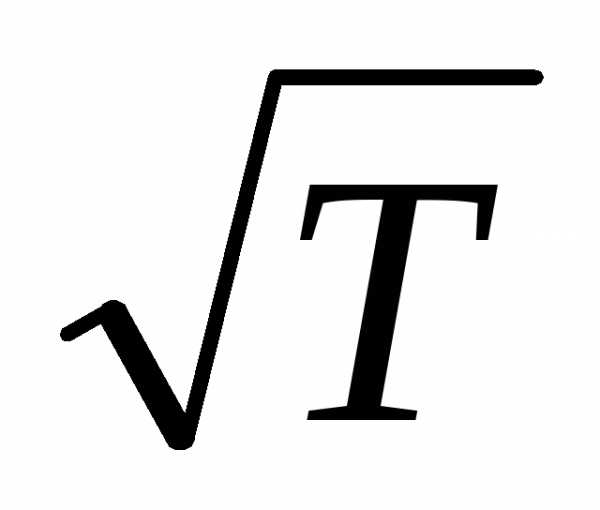 , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
, что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью. В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н.Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
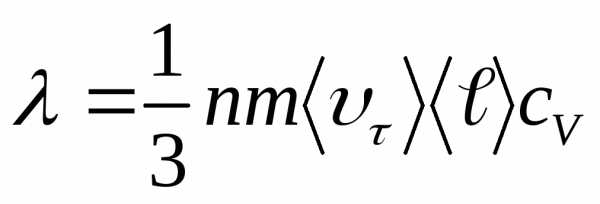 (14.13)
(14.13)
(n – концентрация атомов, m -масса атома, <ℓ> -средняя длина свободного пробега электрона, cV-удельная теплоёмкость).
Для одноатомного газа
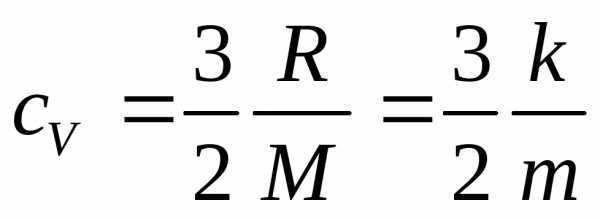
(k -постоянная Больцмана, М –молярная масса).
Тогда
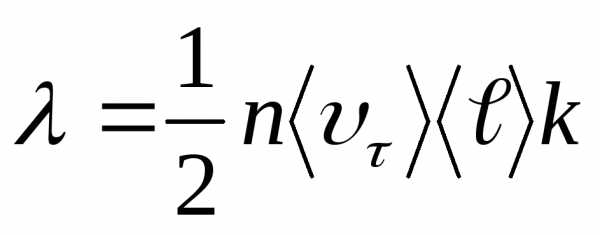 (14.14)
(14.14)
Из уравнений (14.7) и (14.14) находим отношение теплопроводности и электропроводности металла:
(14.15)
Из кинетической теории газов известно, что 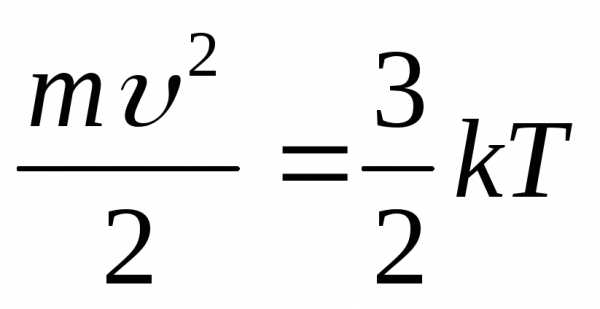 , тогда
, тогда
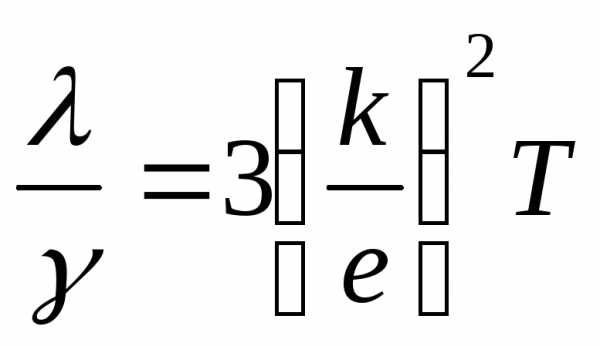 (14.16)
(14.16)
( k и е – постоянные величины).
Поэтому отношение теплопроводности и электропроводности металла пропорционально термодинамической температуре, что и было установлено законом Видемана-Франца. Так как k =1,38∙10-23Дж/К; е = 1,6∙10-19Кл, то
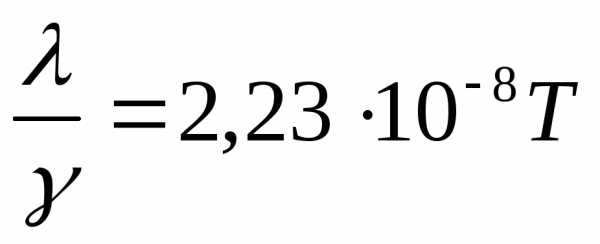 (14.17)
(14.17)
Закон Видемана-Франца для большинства металлов выполняется при температуре 100-400 К, но при низкой температуре закон существенно нарушается. Имеются металлы (бериллий, марганец) которые совсем не подчиняются закону Видемана-Франца. Выход из непреодолимых противоречий был найден в квантовой электронной теории металлов.
studfiles.net
Зависимость сопротивления проводника от температуры. Сверхпроводимость
Зависимость сопротивления проводника от температуры. Сверхпроводимость
«Физика - 10 класс»
Какую физическую величину называют сопротивлением От чего и как зависит сопротивление металлического проводника?
Различные вещества имеют разные удельные сопротивления. Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0 °С, сопротивление проводника равно R0, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.
Температурный коэффициент сопротивления — величина, равная отношению относительного изменения сопротивления проводника к изменению его температуры.
Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К (на 1 °С).
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов
У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается. Для них α < 0. Например, для 10%-ного раствора поваренной соли α = -0,02 К-1.
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения Вычисления приводят к следующему результату:
ρ = ρ0(1 + αt), или ρ = ρ0(1 + αΔТ), (16.2)
где ΔТ — изменение абсолютной температуры.
Так как а мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 16.2).
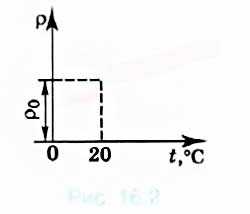
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10-5 К-1; удельное сопротивление Константина велико: ρ ≈ 10-6 Ом • м. Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10-3 К-1. Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления.
На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы. Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.
Обычно в качестве основного рабочего элемента термометра сопротивления берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость.
Сопротивление металлов уменьшается с уменьшением температуры. Что произойдёт при стремлении температуры к абсолютному нулю?
В 1911 г. голландский физик X. Камерлинг-Оннес открыл замечательное явление — сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,1 К очень резко падает до нуля (рис. 16.3).
Явление падения до нуля сопротивления проводника при критической температуре называется сверхпроводимостью.
Открытие Камерлинг-Оннеса, за которое в 1913 г. ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже было открыто много других сверхпроводников.
Сверхпроводимость многих металлов и сплавов наблюдается при очень низких температурах — начиная примерно с 25 К. В справочных таблицах приводятся температуры перехода в сверхпроводящее состояние некоторых веществ.
Температура, при которой вещество переходит в сверхпроводящее состояние, называется критической температурой.
Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово имеет структуру алмаза с кубической кристаллической решёткой и является полупроводником, а белое олово обладает тетрагональной элементарной ячейкой и является серебристо-белым, мягким, пластичным металлом, способным при температуре, равной 3,72 К, переходить в сверхпроводящее состояние.
У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств, так что правильнее говорить не о сверхпроводящем состоянии, а об особом, наблюдаемом при низких температурах состоянии вещества.
Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается.
Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения тепла в сверхпроводящей обмотке не происходит.
Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано и током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превысить которое, не нарушая сверхпроводящего состояния, нельзя.
Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих механическую энергию струи раскалённого ионизованного газа, движущегося в магнитном поле, в электрическую энергию.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г. американскими учёными Дж. Бардиным, Л. Купером, Дж. Шриффером и советским учёным, академиком Н. Н. Боголюбовым.
В 1986 г. была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов (керамики) с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).
Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике, конструировании ЭВМ. Сейчас прогресс в этой области тормозится необходимостью охлаждения проводников до температур кипения дорогого газа — гелия.
Физический механизм сверхпроводимости довольно сложен. Очень упрощённо его можно объяснить так: электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов. Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Надо надеяться, что удастся создать сверхпроводники и при комнатной температуре. Генераторы и электродвигатели станут исключительно компактными (уменьшатся в несколько раз) и экономичными. Электроэнергию можно будет передавать на любые расстояния без потерь и аккумулировать в простых устройствах.
Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электрический ток в различных средах - Физика, учебник для 10 класса - Класс!ная физика
Электрическая проводимость различных веществ. Электронная проводимость металлов --- Зависимость сопротивления проводника от температуры. Сверхпроводимость --- Электрический ток в полупроводниках. Собственная и примесная проводимости --- Электрический ток через контакт полупроводников с разным типом проводимости. Транзисторы --- Электрический ток в вакууме. Электронно-лучевая трубка --- Электрический ток в жидкостях. Закон электролиза --- Электрический ток в газах. Несамостоятельный и самостоятельный разряды --- Плазма --- Примеры решения задач по теме «Электрический ток в различных средах»
class-fizika.ru
Изучение зависимости сопротивления металлов от температуры
Цель работы:оценить температурный коэффициент сопротивления
Приборы и принадлежности: исследуемые проводники, термометр,
мост.
Из квантовой теории известно, что электроны обладают волновыми свойствами. Электрон в металле должен рассматриваться как волна и, поскольку длина волны электрона по порядку величины сравнима с постоянной решетки, он должен испытывать сильную дифракцию (рассеяние). Отсюда ясно, что именно волновые свойства электрона определяют его поведение в металле (следовательно, сопротивление металла).
Квантовая теория выяснила, что если кристалл абсолютно лишен искажений, его решетка идеально периодична, т.е. все ионы неподвижны и находятся в узлах решетки, то электронная волна проходит через решетку почти так же, как через пустое пространство.
Зато любые нарушения периодичности решетки - дефекты, примеси, тепловые колебания - являются причиной рассеивания электронных волн. Это рассеяние уменьшает ток, т.е. вызывает электрическое сопротивление. Повышение температуры, усиливающее тепловые колебания ионов решетки, должно усиливать рассеяние электронных волн, и, следовательно, увеличивать сопротивление металла, что и наблюдается в действительности.
Исходя из квантовых представлений о природе сопротивления, можно дать рекомендации по созданию металлических проводников с большим сопротивлением. В качестве таких проводников надо брать сплавы с возможно более «испорченной» решеткой. Такими сплавами являются, например, нихром, константан, манганин и др. Они имеют удельное сопротивление в несколько десятков раз больше, чем у серебра.
Поскольку электрон рассеивается только на "испорченных местах" решетки, средняя длина его свободного пробега гораздо больше, чем постоянная решетка. При комнатной температуре см. Это дает правильную по порядку величины проводимость.
Разумеется, зависит от температуры, уменьшаясь с её повышением (чем выше температура, тем больше рассеяние на колебаниях решетки). В области температур, далекой от абсолютного нуля, длина свободного пробега обратно пропорциональна температуре:
. (1)
Опыт показывает, что в первом приближении изменение сопротивления с температурой описывается линейным законом:
(2)
где R0- сопротивление проводника при 00С, t- температура проводника в оС, α-температурный коэффициент сопротивления, который показывает относительное изменение сопротивления при изменении температуры на один Кельвин.
Для чистых металлов:
В общем случае α зависит от температуры. Однако для многих металлов при не слишком больших температурах этим можно пренебречь.
Порядок выполнения работы
Исследуемый проводник R помещают в пробирку П с маслом и опускают в сосуд С с водой, установленный на электрическом нагревателе Н. Отсчет температуры производится по показаниям термометра Т (рис.1).
Сначала мостом М измеряют сопротивление проводника при комнатной температуре. Затем включается нагреватель и, по мере нагрева, производятся измерения сопротивления через каждые 5-6 градусов. Для большей точности нагреватель на время измерений можно отключить. Измерения проводят до температуры 80-90°С. Полученные результаты заносят в таблицу.
| Т, °С | |||||||||
| R, Ом |
По полученным данным строятся графики сопротивления как функции температуры. Поскольку изменения сопротивления невелики, то для большей наглядности и точности ось сопротивлений следует "сдвинуть", выбрав затем достаточно удобный масштаб. Данные измерений наносятся на график в виде точек, затем "на глаз" проводится прямая линия, проходящая как можно ближе ко всем нанесенным точкам (рис.2).Продолжив график до пересечения с осью сопротивлений, находим значение сопротивления при 0°С, т.е. Rо. Зная R0 и взяв из графика какое-либо значение Rt и соответствующую ему температуру (для большей точности следует брать это значение при достаточно большой температуре), вычисляют значение α:
(3)
Задачи
1. Сопротивление медного проводника при 200С равно 50 Ом. Его сопротивление при – 300С (α = 0,004ºС-1) равно:
Ответы: а) 100 Ом; б) 30 Ом; в) 40,74 Ом; г) 56,71 Ом; д) 81,13 Ом.
2. Сопротивление угольного проводника при температуре 00С равно 15 Ом, а при температуре 2200С оно равно 13,5 Ом. Температурный коэффициент сопротивления угля равен…
Ответы: а) 0,0028 ºС-1; б) - 0,00045 ºС-1; в) 0,004 ºС-1; г) 0,00015 ºС-1;
д) нет ответа.
3. На сколько следует повысить температуру медного проводника, взятого при 0ºС, чтобы его сопротивление увеличилось в 3 раза? (α=0,0033ºС-1)
4. Сопротивление вольфрамовой нити при t1 = 100С равно R1 = 0,53 Ом. Когда по нити идет ток, сопротивление возрастет до R2 = 6,22 Ом. Какова температура нити, если температурный коэффициент сопротивления вольфрама α=0,0060С-1?
5. Металлическую проволоку, включенную в цепь последовательно с амперметром, подогрели на спиртовой горелке. Амперметр показал при этом уменьшение тока. На основании этого опыта объясните, как изменяется сопротивление металлов при изменении температуры?
Контрольные вопросы
1. Как объясняет квантовая теория сопротивление металлов?
2. Что называется температурным коэффициентом сопротивления и в каких единицах он измеряется?
3. Как зависит сопротивление металла от температуры?
4. Что такое R0?
5. Для чего строят график рис. 2?
Литература
1. Савельев И. В. Курс общей физики. М.: Наука. Т.2, 1982. § 34.
2. Трофимова Т. И. Курс физики. М.: Высшая школа. 2002, § 98.
3. Бондарев Б. В., Калашников Н. П., Спирин Г. Г. Курс общей физики. М.: Высшая школа. 2003, кн. 2. § 4.2
Лабораторная работа 2.4
stydopedia.ru
Изучение зависимости сопротивления металлов от температуры
⇐ ПредыдущаяСтр 4 из 16Следующая ⇒Цель работы:оценить температурный коэффициент сопротивления
Приборы и принадлежности: исследуемые проводники, термометр,
мост.
Из квантовой теории известно, что электроны обладают волновыми свойствами. Электрон в металле должен рассматриваться как волна и, поскольку длина волны электрона по порядку величины сравнима с постоянной решетки, он должен испытывать сильную дифракцию (рассеяние). Отсюда ясно, что именно волновые свойства электрона определяют его поведение в металле (следовательно, сопротивление металла).
Квантовая теория выяснила, что если кристалл абсолютно лишен искажений, его решетка идеально периодична, т.е. все ионы неподвижны и находятся в узлах решетки, то электронная волна проходит через решетку почти так же, как через пустое пространство.
Зато любые нарушения периодичности решетки - дефекты, примеси, тепловые колебания - являются причиной рассеивания электронных волн. Это рассеяние уменьшает ток, т.е. вызывает электрическое сопротивление. Повышение температуры, усиливающее тепловые колебания ионов решетки, должно усиливать рассеяние электронных волн, и, следовательно, увеличивать сопротивление металла, что и наблюдается в действительности.
Исходя из квантовых представлений о природе сопротивления, можно дать рекомендации по созданию металлических проводников с большим сопротивлением. В качестве таких проводников надо брать сплавы с возможно более «испорченной» решеткой. Такими сплавами являются, например, нихром, константан, манганин и др. Они имеют удельное сопротивление в несколько десятков раз больше, чем у серебра.
Поскольку электрон рассеивается только на "испорченных местах" решетки, средняя длина его свободного пробега гораздо больше, чем постоянная решетка. При комнатной температуре см. Это дает правильную по порядку величины проводимость.
Разумеется, зависит от температуры, уменьшаясь с её повышением (чем выше температура, тем больше рассеяние на колебаниях решетки). В области температур, далекой от абсолютного нуля, длина свободного пробега обратно пропорциональна температуре:
. (1)
Опыт показывает, что в первом приближении изменение сопротивления с температурой описывается линейным законом:
(2)
где R0- сопротивление проводника при 00С, t- температура проводника в оС, α-температурный коэффициент сопротивления, который показывает относительное изменение сопротивления при изменении температуры на один Кельвин.
Для чистых металлов:
В общем случае α зависит от температуры. Однако для многих металлов при не слишком больших температурах этим можно пренебречь.
Порядок выполнения работы
Исследуемый проводник R помещают в пробирку П с маслом и опускают в сосуд С с водой, установленный на электрическом нагревателе Н. Отсчет температуры производится по показаниям термометра Т (рис.1).
Сначала мостом М измеряют сопротивление проводника при комнатной температуре. Затем включается нагреватель и, по мере нагрева, производятся измерения сопротивления через каждые 5-6 градусов. Для большей точности нагреватель на время измерений можно отключить. Измерения проводят до температуры 80-90°С. Полученные результаты заносят в таблицу.
| Т, °С | |||||||||
| R, Ом |
По полученным данным строятся графики сопротивления как функции температуры. Поскольку изменения сопротивления невелики, то для большей наглядности и точности ось сопротивлений следует "сдвинуть", выбрав затем достаточно удобный масштаб. Данные измерений наносятся на график в виде точек, затем "на глаз" проводится прямая линия, проходящая как можно ближе ко всем нанесенным точкам (рис.2).Продолжив график до пересечения с осью сопротивлений, находим значение сопротивления при 0°С, т.е. Rо. Зная R0 и взяв из графика какое-либо значение Rt и соответствующую ему температуру (для большей точности следует брать это значение при достаточно большой температуре), вычисляют значение α:
(3)
Задачи
1. Сопротивление медного проводника при 200С равно 50 Ом. Его сопротивление при – 300С (α = 0,004ºС-1) равно:
Ответы: а) 100 Ом; б) 30 Ом; в) 40,74 Ом; г) 56,71 Ом; д) 81,13 Ом.
2. Сопротивление угольного проводника при температуре 00С равно 15 Ом, а при температуре 2200С оно равно 13,5 Ом. Температурный коэффициент сопротивления угля равен…
Ответы: а) 0,0028 ºС-1; б) - 0,00045 ºС-1; в) 0,004 ºС-1; г) 0,00015 ºС-1;
д) нет ответа.
3. На сколько следует повысить температуру медного проводника, взятого при 0ºС, чтобы его сопротивление увеличилось в 3 раза? (α=0,0033ºС-1)
4. Сопротивление вольфрамовой нити при t1 = 100С равно R1 = 0,53 Ом. Когда по нити идет ток, сопротивление возрастет до R2 = 6,22 Ом. Какова температура нити, если температурный коэффициент сопротивления вольфрама α=0,0060С-1?
5. Металлическую проволоку, включенную в цепь последовательно с амперметром, подогрели на спиртовой горелке. Амперметр показал при этом уменьшение тока. На основании этого опыта объясните, как изменяется сопротивление металлов при изменении температуры?
Контрольные вопросы
1. Как объясняет квантовая теория сопротивление металлов?
2. Что называется температурным коэффициентом сопротивления и в каких единицах он измеряется?
3. Как зависит сопротивление металла от температуры?
4. Что такое R0?
5. Для чего строят график рис. 2?
Литература
1. Савельев И. В. Курс общей физики. М.: Наука. Т.2, 1982. § 34.
2. Трофимова Т. И. Курс физики. М.: Высшая школа. 2002, § 98.
3. Бондарев Б. В., Калашников Н. П., Спирин Г. Г. Курс общей физики. М.: Высшая школа. 2003, кн. 2. § 4.2
Лабораторная работа 2.4
Читайте также:
lektsia.com
Зависимость сопротивления металлических проводников от температуры. Температурный коэффициент сопротивления | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Сопротивление проводников зависит от вещества, из которого они изготовлены, и их геометрических размеров
R = ρ • l / S,
где ρ — удельное сопротивление вещества, из которого изготовлен проводник; l —длина проводника; S — площадь поперечного сечения проводника.
Сопротивление проводников входит в закон Ома для однородного участка цепи I = U / R, из которого и может быть определено R = U / I.
Из последней формулы выходит, что сопротивление проводника постоянно, поскольку, в соответствии с законом Ома, во сколько раз увеличиваем напряжение на концах проводника, во столько же раз возрастает и сила тока в нем.
Но на практике можно наблюдать и другие явления. Составим электрическую цепь, схема которой показана на рис. 7.2. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, например автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напряжение U1 и отмечаем силу тока I1. Если теперь увеличить напряжение, например в 2 раза (U2 = 2U1), то по закону Ома и сила тока должна увеличиться в 2 раза (I2 = 2I1). Однако амперметр показывает силу тока значительно меньшую, чем 2I1. Следовательно, в данном случае закон Ома не выполняется.
| Рис. 7.2. Электрическая цепь с лампой накала |
Возникло несоответствие между вашими предшествующими знаниями и новым для вас фактом — закон Ома не всегда справедлив. Такое несоответствие в науке называется проблемой.
Проблема (гр. — задача, затруднение) — сложный теоретический или практический вопрос, требующий решения.
Можно высказывать разные предположения, что является попыткой объяснить наблюдаемое явление. Однако в ходе опыта бросается в глаза, что при увеличенном напряжении лампа светится ярче, чем в первом случае. Это является свидетельством того, что температура спирали лампы во втором случае выше, чем в первом. Возможно, именно изменение температуры является причиной изменения сопротивления металлической спирали лампы.
| Рис. 7.3. Исследование зависимости сопротивления металлического проводника от температуры |
Как же можно проверить такое предположение (гипотезу)? Составляем электрическую цепь (рис. 7.3), в которой есть металлический проводник в виде спирали, например пружинка от шариковой ручки, и устанавливаем в цепи ток определенной силы. Нагревая спираль в пламени свечи или спички, заметим:
при нагревании спирали и при постоянном напряжении сила тока в цепи уменьшается, что свидетельствует об увеличении сопротивления спирали при повышении ее температуры.
Тщательные исследования показывают, что сопротивление металлических проводников зависит от их температуры практически линейно
R = R0(1 + αt°),
где R0 — сопротивление проводника при 0 °C или +20 °C (это удобнее для техники). График такой зависимости представлен на рис. 7.4.
| Рис. 7.4. График зависимости сопротивления металлического проводника от температуры |
Если иметь в виду, что размеры металлов при нагревании изменяются мало, то соответствующую формулу можно записать и для удельного сопротивления металлических проводников
ρ = ρ0(1 + αt°).
Рассмотрим, что означает коэффициент в полученных формулах. Если при 0°C сопротивление проводника R0, а при t° C сопротивление его R, то относительное изменение сопротивления, как показывает эксперимент, (R — R0) / R0 = αt° C. Материал с сайта http://worldofschool.ru
Коэффициент пропорциональности называется температурным коэффициентом сопротивления, который характеризует зависимость сопротивления вещества от его температуры.
Температурный коэффициент сопротивления равен относительному изменению сопротивления проводника при изменении его температуры на 1 К.
Для всех металлических проводников α > 0 и мало зависит от температуры.
Почему же возрастает сопротивление металлических проводников с повышением температуры? Дело в том, что при нагревании металла возрастает интенсивность колебаний ионов кристаллической решетки и скорость хаотического движения электронов.
Электроны чаще сталкиваются с ионами, что и уменьшает скорость их направленного движения, которое и является электрическим током.
В технике зависимость сопротивления металлических проводников от температуры используется в термометрах сопротивления.
Датчик температуры (например, платиновая проволочка) устанавливается в тех точках, где необходимо измерять температуру, а его сопротивление измеряют омметром, шкала которого градуируется в единицах температуры. Таких датчиков, при необходимости, может быть любое количество, а измерительный прибор — один.
На этой странице материал по темам:Зависимость сопротивления от температуры в вакууме формула
Зависимость сопротивления металлических проводников от температуры
Датчик температуры сопротивление металла при нагревании
Электрический ток в вакууме зависимость сопротивления от температуры
Зависимость удельного сопротивления от температуры в вакууме
От чего и как зависит сопротивление металлических проводников при постоянной температуре?
Как зависит сопротивление металлических проводников от температуры?
Где используется зависимость сопротивления металлических проводников от температуры?
worldofschool.ru
2. Температурная зависимость сопротивления металлов
Согласно классической теории металлов газ свободных электронов движется хаотично, и электроны претерпевают многочисленные столкновения с ионами кристаллической решетки. При включении электрического поля движение электронов становиться упорядоченным, однако, в результате столкновений электронов с ионами решетки их движение тормозится, что и является причиной наличия сопротивления. С ростом температуры возрастает вероятность столкновений электронов с решеткой, поэтому согласно классическим представлениям сопротивление металлов возрастает с ростом температуры11.
Однако согласно расчетам выполненным в рамках классической теории электропроводности сопротивление должно повышаться с ростом температуры пропорционально Т-½, в то время как на опыте сопротивление растет пропорционально Т. Расчет электропроводности основанный на квантовой статистике Ферми-Дирака дал правильную температурную зависимость сопротивления металлов от температуры. Согласно квантовым представлениям свободный электрон в металле обладает свойствами волны. Такая волна в идеальной решетке кристалла должна была бы двигаться беспрепятственно. Однако на практике происходит рассеивание волны на неоднородностях кристаллической решетки. В первую очередь такие искажения решетки возникают в результате тепловых колебаний атомов возле положения равновесия12. Таким образом, основная причина зависимости сопротивления металлов от температуры состоит в том, что электроны рассеиваются на колебаниях решетки, величина которых возрастает с ростом температуры.13
Унекоторых металлов (ртуть, свинец) при температуре, близкой к абсолютному нулю сопротивление скачком уменьшается до нуля (явление сверхпроводимости). У специальных сплавов, таких как константан (60% Cu, 40% Ni) и манганин (86% Cu, 2% Ni, 12% Mn) сопротивление очень слабо зависит от температуры. Эти сплавы применяются при изготовлении высокоточных сопротивлений. Зависимость удельного сопротивления (удельной проводимости ) от температуры для некоторых материалов показана на рис. 6.3. Ниже 20 К сопротивление меди не меняется, что связано с дефектами решетки, а чистый свинец при 7.3 К переходит в сверхпроводящее состояние.
Температурным коэффициентом сопротивления называется отношение относительного изменения сопротивления к изменению температуры14.
(6.2)
При нелинейной зависимости сопротивления от температуры более корректным является определение
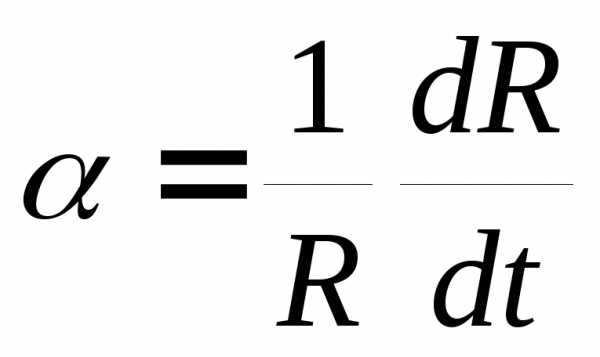
Для определенности, в таблицах значения величин приводятся при температуре 20С. Зависимость сопротивления от температуры для металлов описывается выражением
Rt = R20[1+(t - 20C)] (6.3)
здесь Rt – сопротивление проводника при температуре t, R20 - сопротивление проводника при 20C. Температурные коэффициенты для некоторых металлов и сплавов при 20С приведены в таб. 1.
Пользуясь экспериментальным графиком зависимости сопротивления от температуры и определив тангенс угла наклона прямой линии (выражение (6.2)) можно найти .
Таблица 1
| Металл, сплав15 | , 10-3 К-1 |
| Медь | 4.3 |
| Железо | 6.5 |
| Нихром | 0.1 |
| Константан | 0.03 |
| Манганин | 0.02 |
studfiles.net












