Закон Ома в дифференциальной форме. Закон ома в дифференциальной форме формула

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника.

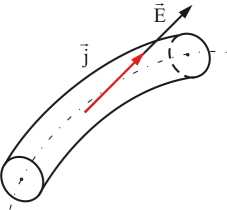
Вывод формулы Закона Ома в дифференциальной форме

Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

К концу пробега скорость упорядоченного движения достигнет значения

Тут t — среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости. В этом приближении

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Полученную формулу подставим в

И у нас получилось

В Формуле мы использовали :

— Вектор плотности тока

— Удельная проводимость

— Вектор напряжённости электрического поля

— среднее значение длины свободного пробега

— скорость теплового движения электронов

xn--b1agsdjmeuf9e.xn--p1ai

Закон Ома в дифференциальной форме

Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

(7.6.1)

Для однородного линейного проводника выразим R через ρ:

(7.6.2)

ρ – удельное объемное сопротивление; [ρ] = [Ом·м].

Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.

В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля коллинеарны (рис. 7.6).

Рис. 7.6

Исходя из закона Ома (7.6.1), имеем:

А мы знаем, что или . Отсюда можно записать

(7.6.3)

это запись закона Ома в дифференциальной форме.

Здесь – удельная электропроводность.

Размерность σ – [].

Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :

Обозначим , тогда ;

(7.6.4)

Теперь, если удельную электропроводность σ выразить через е, n и b: то вновь получим выражение закона Ома в дифференциальной форме:

Закон Ома для неоднородного участка цепи Работа и мощность тока. Закон Джоуля – Ленца

ens.tpu.ru

Закон Ома в дифференциальной форме

При детальном изучении силы тока в сильно неоднородном проводнике закон Ома в обычной форме не подходит, так как он не учитывает локальные параметры проводника. Рассмотрим, например, проводник у которого вдоль оси значительно изменяется электрическое сопротивление и его поперечное сечение. Очевидно, что такой проводник можно представить, как один резистор с интегральным сопротивлением (такое, которое одновременно учитывает все неравномерности), однако если встает вопрос как именно течет ток в таком резисторе, то обычная формулировка закона Ома не применима.

Давайте выведем закон Ома в дифференциальной форме. Рассмотрим проводник с переменным поперечным сечением и сопротивлением вдоль оси z (см. рисунок 1). Разделим этот проводник по середине на две части. Затем полученные два кусочка разделим ещё на две части. Заметим, что при разбиении, каждая часть становится более однородной, нежели проводник в совокупности (см. рис. 2).

Рис.1. Проводник с переменным поперечным сечением и сопротивлением вдоль оси

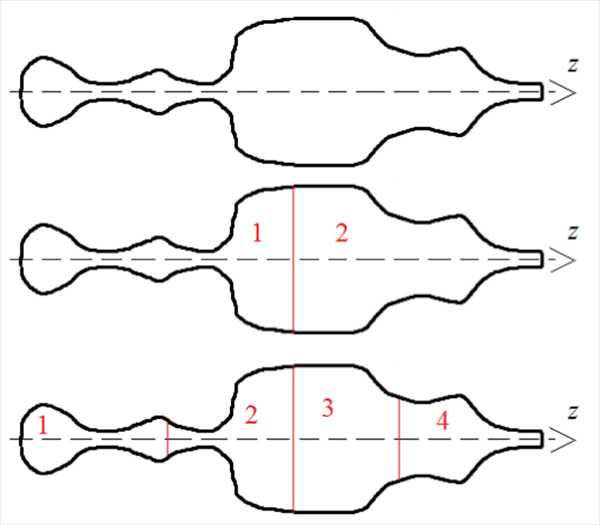
Рис. 2. Разбиение неоднородного проводника на части

А теперь, внимание! Делим полученные кусочки на две части и так далее до бесконечности! Т.е. проводник теперь состоит из бесконечного числа бесконечно малых проводников. Интерес представляет такой бесконечно малый кусочек, ведь он строго однороден. У него постоянная толщина и постоянное сопротивление. Вообще такой кусочек проводника разумно было бы показать в виде тонкой вертикальной линии, но для наглядности покажем, что проводник толщину имеет хоть она бесконечно мала (см. рис. 3).

Рис. 3. Бесконечно малый проводник

Итак, закон Ома в дифференциальной форме связывает плотность тока, с удельной проводимостью и напряженностью для бесконечно малого участка проводника.

Строгая формулировка закона Ома в дифференциальной может быть записана так: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.

Выведем формулу закона Ома в дифференциальной форме. Запишем связь между потенциальном и напряжённостью

zakon-oma.ru

Закон Ома. Закон Ома в дифференциальной форме

Закон Ома. Закон Ома в дифференциальной форме.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источникаили электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

— ЭДС источника напряжения(В),
— сила тока в цепи (А),
— сопротивление всех внешних элементов цепи (Ом),
— внутреннее сопротивление источника напряжения (Ом).

Из закона Ома для полной цепи вытекают следствия:

При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S).

(7.6.3)

это запись закона Ома в дифференциальной форме.

Здесь – удельная электропроводность.

Размерность σ – [].

Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :

Обозначим , тогда ;

(7.6.4)

studfiles.net

Закон ома в дифференциальной форме

Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению:

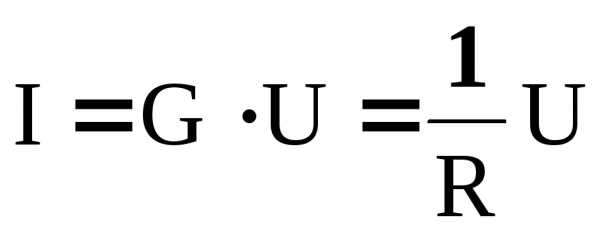, (11)

где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением

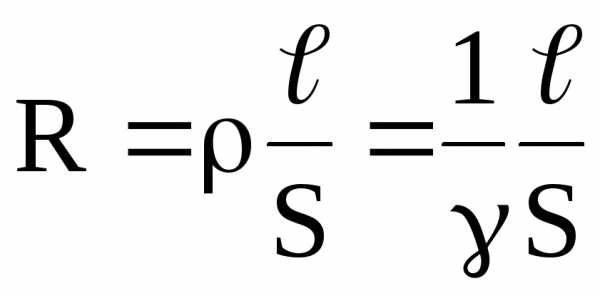, (12)

где γ = 1 / ρ – удельная электропроводность материала, ρ – удельное сопротивление, S – площадь поперечного сечения проводника, 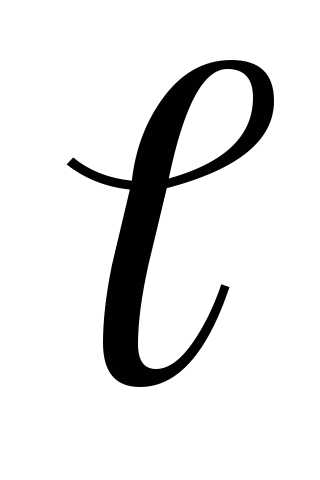– его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид:

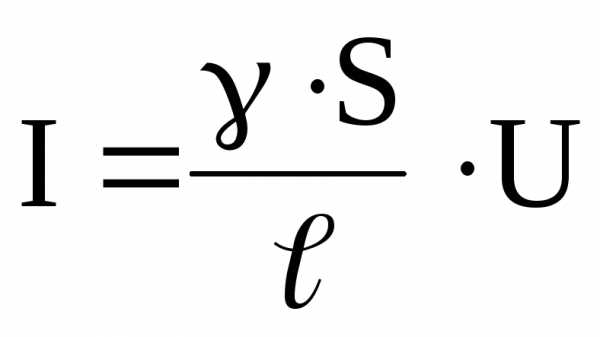. (13)

Теперь для плотности тока (2) с учётом, что – напряжённость поля в проводнике, получим:

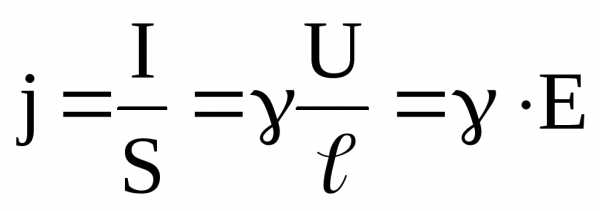. (14)

Выражение (14) в векторной форме это закон Ома в дифференциальной форме:

. (15)

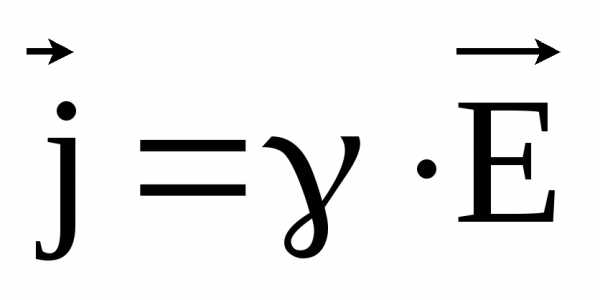
Получим в дифференциальной форме закон Джоуля-Ленца. Количество теплоты, выделяющееся в элементе проводника, объёмом 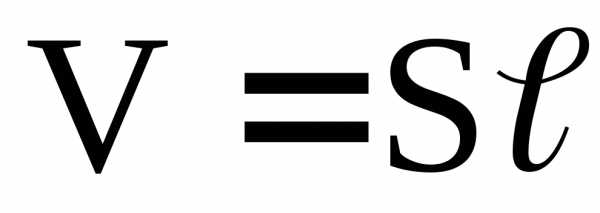за времяdt:

. (16)

Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет:

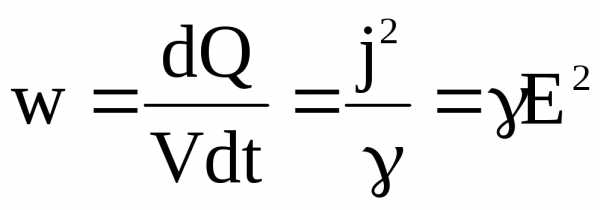. (17)

Эта величина называется удельной тепловой мощностью тока.

Э л е к т р и ч е с к и й т о к в м е т а л л а х

Ток в металлах представляет собой движение не связанных с ионами кристаллической решеткой электронов. Первое опытное подтверждение того, что в создании тока в металлах ионы участия не принимают, было получено еще в 1901 г. в опыте немецкого ученого К. Рикке (1845 – 1915). В течение года ток пропускали через три последовательно составленных и тщательно пришлифованных цилиндраAl – Cu – Al. При этом в телах не было обнаружено даже мизерного переноса вещества или каких-либо химических изменений. Т.е. металлы относятся к проводникам первого рода. Впоследствии этот факт был подтвержден другими опытами.

Сопротивление чистых металлических проводников при не очень низких температурах:

R = R0 (1+ α·t0C), откуда

R = α R0T, (18)

где α = 1/273 К-1 – температурный коэффициент сопротивления, R0 – сопротивление проводника при 00 С.

В области низких температур (Т < 20 К) сопротивление многих металлов (Al, Pb, Zn) и их сплавов резко падает до нуля. Это явление сверхпроводимости.

Электрический ток в электролитах и расплавах

Если в электролит или расплав ввести две твердотельных пластинки (электроды) и подать на них напряжение, то возникает электрический ток, который создаётся направленным движением ионов. Достигнув соответствующих электродов, ионы отдают или приобретают электроны и превращаются в нейтральные атомы или молекулы. В результате химических реакций вторичные продукты либо оседают на электродах, либо переходят в раствор. Явление осаждения составных частей электролита на электродах получило название электролиза. Материалы, в которых при прохождении тока происходят химические превращения, относятся к проводникам второго рода. Т.е. электролиты и расплавы это проводники второго рода.

Количественно электролиз описывается законами Фарадея:

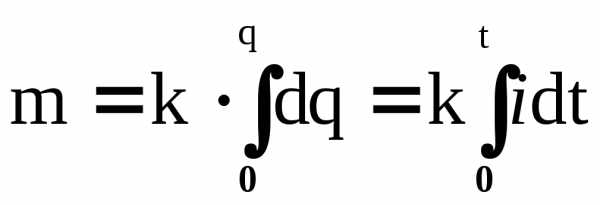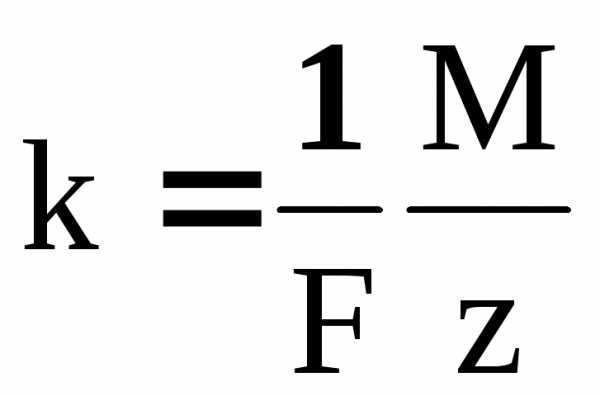,, (19)

где m – масса осевшего на электроде вещества, k – его электрохимический эквивалент, i = f(t) – сила тока, t – время его протекания, F – число Фарадея (F = 96,497∙106 Кл/моль.), М – молярная масса вещества, z – валентность, F/z – называется химическим эквивалентом вещества.

Если величина тока I в процессе электролиза не меняется, то (18) принимает вид:

(20)

Ионы, как носители электрического заряда в электролитах, образуются в растворах солей, щелочей или кислот в воде и некоторых других жидкостях в результате электролитической диссоциации.

В растворе каждая полярная молекула растворенного вещества окружена дипольными молекулами растворителя. Причем к положительно заряженной части молекулы растворенного вещества молекулы растворителя повернуты своими «отрицательными» концами, а к отрицательно заряженной соответственно «положительными». Это ослабляет силы электростатического притяжения ионов, образующих молекулу растворенного вещества. В результате теплового движения может произойти разрыв связи. Образующиеся ионы (анионы и катионы) начинают странствовать по раствору. При сближении на достаточно малое расстояние анион и катион могут снова соединится. Этот процесс называется рекомбинация (или молизация). В растворе процессы диссоциации и рекомбинации идут параллельно. В конечном итоге в растворе при постоянных внешних условиях устанавливается динамическое равновесие. Этому состоянию соответствует определенная степень диссоциации, которую принято характеризовать коэффициентом диссоциации – α, который показывает долю распавшихся молекул растворенного вещества – α = n' / n0, где n0 – концентрация растворённого вещества, n' – концентрация распавшихся молекул.

При невысоких температурах ионы бывают окружены облепившими их ионами растворителя. Это явление получило название сольватации (для водных растворов – гидратации), а сам комплекс из иона и удерживаемой его силовым полем оболочки из молекул растворителя называют сольватом.

Рассмотрим механизм электролитической проводимости. При наложении электрического поля на электролит на каждый ион будет действовать кулоновская сила Fк = Еq, которая вызовет ускоренное упорядоченное движение. Ионы, а тем более сольваты, из-за своих раз-меров испытывают при движении сопротивление пропорциональное скорости упорядоченного движения – υ: Fс = kυ. Скорость υ будет расти пока кулоновская сила Fк не станет равной силе сопротивления Fс: Еq = kυ. Откуда: 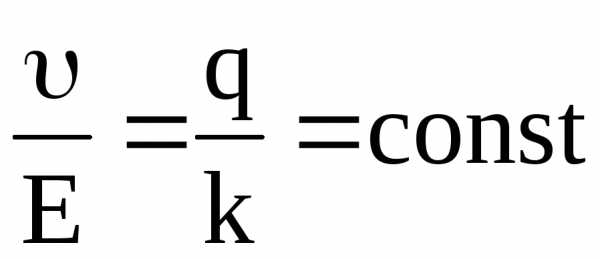, т.к. для данного раствора k =const и q = const. Отношение

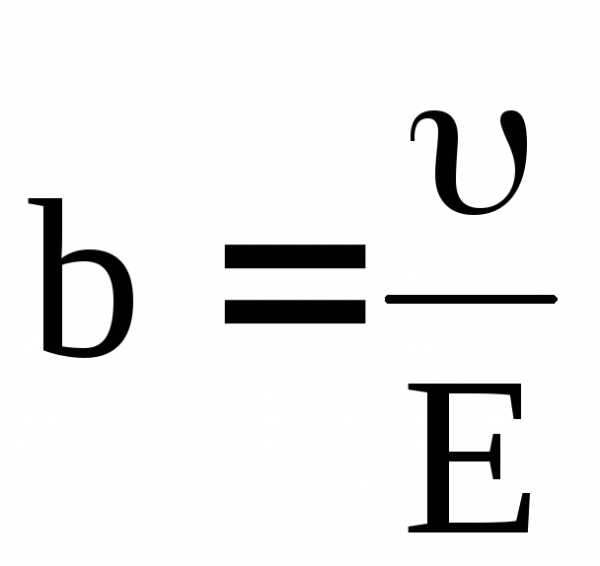(21)

называется подвижностью ионов, которая представляет среднюю

скорость дрейфа заряженных частиц в поле с напряженностью 1 В/м). [b] = м2 / (В·с). Подвижность ионов b зависит от их природы, свойств растворителя и температуры. При комнатной температуре для водных растворов подвижность по порядку величины равна 10-8 – 10-7 м2/В∙с.

Для установившегося движения, в соответствии с (5) и учетом (20) плотность тока в электролите будет:

j = (n+ q+ b+ + n- q- b-)Е (22)

Величина в скобках не зависит от напряженности поля – Е. Это значит, ток в электролитах подчиняется закону Ома. Если каждая молекула диссоциирует на два иона, то

j = αnq(b+ + b-)Е. (23)

Выражение

γ = αnq(b+ + b-) (24)

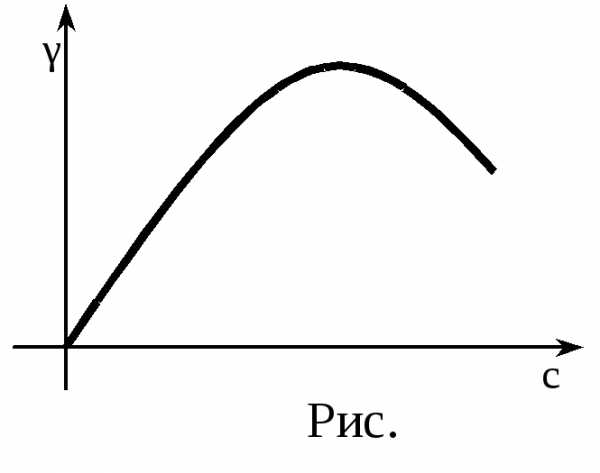
представляет собой электропроводность электролита. Как видно из выражения (23), проводимость электролитов растет с повышением температуры, т.к. при этом увеличивается коэффициент диссоциации и подвижность ионов. Зависимость γ от концентрации довольно сложная (рис.): Для слабых растворов, когда α ≈ 1, γ растет пропорционально с. В дальнейшем с увеличением концентрации коэффициент диссоциации α убывает, поэтому рост проводимости замедляется, а затем даже начинает уменьшаться.

Электрофорез – направленное движение заряженных частиц (ионов, капелек жидкости, взвешенных и коллоидных части) под воздействием электрического поля в какой-то среде. Скорость упорядоченного движения при электрофорезе определяется уравнением Смолуховского:

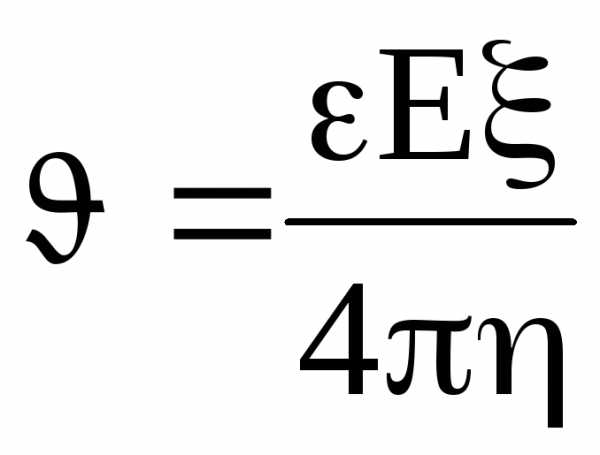, (25)

где ε – диэлектрическая проницаемость среды, Е – напряженность электрического поля, η – вязкость среды, ξ – электрокинетический (дзета) потенциал. (Более подробно материал изложен в лабораторной работе «Электрофорез»)

studfiles.net

Закон Ома в дифференциальной форме

Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):

В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке.

Сопротивление R участка цепи зависит от длины l этого участка, поперечного сечения S и удельного сопротивления проводника ρ. Зависимость сопротивления от материала проводника и его геометрических размеров выражается формулой:

которая справедлива только для проводников постоянного сечения. Для проводников переменного сечения соответствующая формула не будет столь простой. В проводнике переменного сечения сила тока в различных сечениях будет одинаковой, однако плотность тока будет разной не только в различных сечениях, но даже и в различных точках одного и того же сечения. Различное значение будет иметь и напряженность, а, следовательно, и разность потенциалов на концах различных элементарных участков. Усредненные значения I, U и R по всему объему проводника не дают информации об электрических свойствах проводника в каждой его точке.

Для успешного изучения электрических цепей необходимо получить выражение закона Ома в дифференциальной форме с тем, чтобы оно выполнялось в любой точке проводника любой формы и любых размеров.

Зная связь напряженности электрического поля с разностью потенциалов на концах некоторого участка , зависимость сопротивления проводника от его размеров и материала и используя закон Ома для однородного участка цепи в интегральной форме найдем:

Обозначив где σ — удельная электропроводность вещества, из которого сделан проводник, получим:

где — плотность тока. Плотность тока — это вектор, направление которого совпадает с направлением вектора скорости перемещения положительных зарядов. Полученное выражение в векторной форме будет иметь вид:

Оно выполняется в любой точке проводника, по которому течет электрический ток. Для замкнутой цепи следует учесть тот факт, что в ней, кроме напряженности поля кулоновских сил, действуют сторонние силы, создающие поле сторонних сил, характеризующееся напряженностью Ест. С учетом этого закон Ома для замкнутой цепи в дифференциальной форме будет иметь вид:

В таком виде закон Ома входит в систему уравнений Максвелла, представляющую собой фундамент классической электродинамики.

vestishki.ru

О законе Ома: интегральная и дифференциальная формы

Немецкий физик Георг Ом в XIX веке экспериментально вывел основную закономерность, по которой функционируют и проектируются электрические цепи. Она заключается в том, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Данная формулировка описывает закон Ома в интегральной форме.

Дифференциальный вид закона Ома

Действие электродвижущих сил

Работая с электричеством, следует помнить, что сопротивление проводника зависит от его размера, формы и материала, из которого он изготовлен. Поэтому данный показатель при решении теоретических и прикладных задач рассчитывается как отношение длины к площади, умноженное на величину удельного сопротивления материала.

Дополнительная информация. Величина сопротивления также зависит и от температуры, где находится проводник. Как правило, такая зависимость носит линейный характер: чем выше температура, тем больше сопротивление проводящего вещества.

Чтобы в цепи появилось электричество, необходимо наличие в ней свободных заряженных частиц (обычно электронов). Кроме того, они должны обладать способностью перемещаться в определенном направлении (от источника тока к его потребителю, от отрицательно заряженного предмета к месту с положительным зарядом). Такое движение создает электрическое поле. Следовательно, чтобы движение частиц не прекращалось, необходимо энергию этого поля каким-либо образом восполнять.

Если соединить проводом два тела, у одного из которых положительный, а у другого отрицательный заряд, из-за кулоновских сил начнется движение электронов. Однако достаточно быстро такое перемещение прекратится, поскольку разница потенциалов из-за действия законов природы восстановится. Таким образом, наличие в электрической цепи только электростатических сил явно недостаточно, чтобы обеспечить постоянное движение электронов в сети.

Важно! Чтобы поддерживать постоянное наличие тока в сети, необходимо обеспечивать разность потенциалов на ее концах. Естественным образом такую ситуацию создать невозможно. Следовательно, необходимы сторонние силы, которые называются электродвижущими.

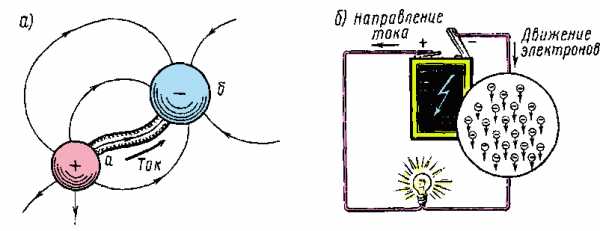
Электродвижущие силы

Благодаря внешнему воздействию, электроны движутся в направлении, противоположном действию электрического поля, за счет чего поддерживается постоянная разница потенциалов. Создает электродвижущие силы источник тока за счет механического действия, химической реакции и так далее. Следовательно, интегрального вида записи закона Ома для описания функционирования электрической цепи недостаточно, поскольку, помимо разницы потенциалов и сопротивления проводника, на движение электронов действует еще ряд факторов. Решить эту задачу позволяет закон Ома в дифференциальной форме.

Движение тока по неоднородным проводникам

Дифференциальная форма записи выявленной Омом закономерности особенно актуальна, когда проводящий элемент по своему составу неоднороден – на всем протяжении движения электронов у него меняется площадь сечения и уровень сопротивления. Это создает определенные сложности при расчете мощности источника тока, параметров изоляции и так далее, чтобы обеспечить стабильность работы сети, а главное – ее безопасность.

Чтобы сформулировать закон Ома в дифференциальной форме, следует представить проводник не как однородное тело, а как набор бесконечного числа бесконечно малых частей. Это позволит считать каждый элемент однородным, а значит, у него постоянная толщина и постоянный уровень сопротивления, и на таком бесконечно малом участке действуют стандартные принципы закона Ома.

Обратите внимание! При записи закономерности Ома в дифференциальном виде необходимо ввести такие понятия, как плотность тока и удельная проводимость, поскольку именно они являются ключевыми для расчета параметров электрической цепи с неоднородным проводником.

Под плотностью понимается векторная величина, которая демонстрирует уровень силы тока, протекающий через единицу площади. Учет плотности приводит к тому, что при неоднородном проводящем элементе в схеме потребуется установка различных дополнительных устройств для выравнивания напряжения и обеспечения стабильности и безопасности работы.

Плотность и проводимость проводника

Удельная проводимость – это величина, обратная удельному сопротивлению, которая позволяет оценить способность единицы какого-либо вещества обеспечивать прохождение через себя электронов. Знание такой характеристики также позволяет корректно спроектировать схему из различных проводников.

Итак, закон Ома является базовым для понимания устройства электрической цепи. Возможность записать его в разных видах позволяет учесть при проектировании схем устройств и приборов толщину, проводимость и другие характеристики материалов. Необходимо отметить, что такая деятельность требует знаний в области высшей математики (владение основами дифференциальных и интегральных вычислений).

Видео

Оцените статью:

elquanta.ru