Каждый закон Кирхгофа прост и понятен. Закон кирхгофа 2 формула

Первый и второй закон Кирхгофа, с примерами

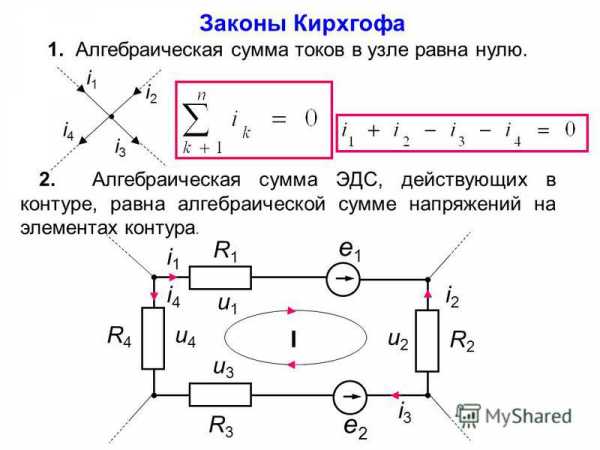
Корректнее данные утверждения, которые в заголовке названы первым и вторым законами Кирхгофа было бы называть правилами Кирхгофа. Данные правила применяют при расчетах параметров сложных разветвленных электрических цепей постоянного тока. Электрические цепи могут содержать множество сопротивлений, источников тока, иметь в своем составе несколько замкнутых контуров и узлов. Параметры, характеризующие подобную цепь можно вычислить, если использовать хорошо известные законы Ома и сохранения заряда. Правила Кирхгофа являются следствиями этих основных законов. Однако при помощи правил Кирхгофа можно существенной упростить процедуру составления уравнений, которые свяжут силы тока, сопротивления и электродвижущие силы (ЭДС) источников в разветвленной цепи постоянного тока. Существует два правила Кирхгофа для электрических цепей постоянного тока. Первое правило Кирхгофа называют правилом узлов. Оно связывает в одно уравнение токи, сходящиеся в узле. Второе правило Кирхгофа относится к замкнутым контурам, которые можно выделить в сложной цепи.

Первый закон Кирхгофа

В разветвлённой электрической цепи в одной точке могут сходиться более двух проводников, по которым текут токи, такую точку цепи называют узлом (разветвлением) цепи. Помня, что сила тока является алгебраической величиной, запишем ее сумму в узле с учетом знаков:

где N – число токов, которые сходятся в узле. Выражение (1) называют первым правилом Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.

Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.

Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи m узлов.

Первое правило Кирхгофа является следствием закона сохранения заряда.

Второй закон Кирхгофа

Второе правило Кирхгофа формулируется для замкнутых контуров, поэтому его называют правилом контуров: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа — это следствие закона Ома.

Примеры решения задач

ru.solverbook.com

2. Второй закон Кирхгофа | 5. Схемы делителей и законы Кирхгофа | Часть1

2. Второй закон Кирхгофа

Второй закон Кирхгофа

Давайте посмотрим на нашу последовательную схему с другой стороны. На этот раз мы пронумеруем все точки схемы, чтобы к ним можно было привязать напряжения:

Если мы подключим вольтметр к точкам 1 и 2 (красный щуп к точке 2, а черный - к точке 1), то он зарегистрирует напряжение +45 В. Обычно дисплей цифрового электроизмерительного прибора знак "+" не показывает, но так как в рамках нашей статьи полярность напряжения имеет очень важное значение, мы будем показывать положительные числа с этим знаком:

Когда рядом с напряжением указываются два символа (символы "2-1" в обозначении U2-1), это означает, что напряжение в первой точке (2) измеряется по отношению ко второй точке (1). Напряжение обозначенное как "Ucd" скажет нам о том, что красный щуп измерительного прибора подсоединяется к точке "с", а черный - к точке "d", то есть это напряжение измеряется в точке "c" относительно точки "d":

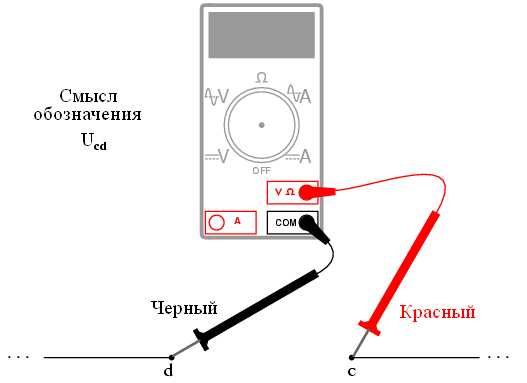
Если мы теперь возьмем тот же самый вольтметр и измерим напряжения на каждом резисторе цепи, обходя ее по часовой стрелке (подсоединяя при этом красный щуп к первой точке, а черный - ко второй), то получим следующие показания:

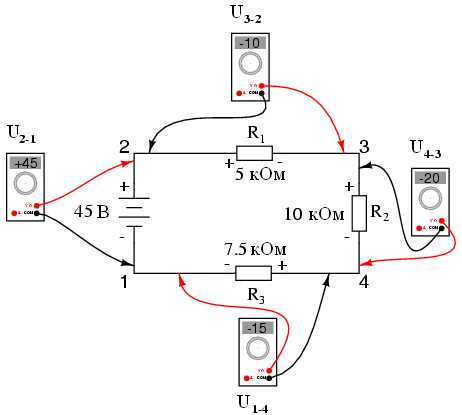
Ранее вы познакомились с одним из принципов последовательной цепи, который гласит что общее напряжение такой цепи складывается из напряжений ее отдельных участков. Но, если при измерении напряжения мы будем учитывать его полярность (математический знак), то пред нами откроется новый аспект этого принципа - суммарное напряжение цепи будет равно нулю:

Этот принцип известен как Второй Закон Кирхгофа или Закон напряжений Кирхгофа (открыт в 1847 году немецким физиком Густавом Кирхгофом), и гласит он следующее:

"Алгебраическая сумма всех напряжений любой замкнутой цепи должна равняться нулю"

Здесь под словом "алгебраическая" понимается учет математического знака (полярности) напряжения, а под словом "замкнутой цепи" - понимается последовательный путь, проложенный вокруг этой цепи из одной ее точки к другим точкам, и обратно к первой точке. В приведенном выше примере замкнутая цепь сформирована последовательностью точек 1-2-3-4-1. Не имеет абсолютно никакого значения с какой точки мы начнем и в каком направлении мы будем двигаться; сумма напряжений все равно будет равняться нулю. В качестве еще одного примера можно подсчитать напряжение в последовательности точек 3-2-1-4-3 этой же схемы:

Все это будет более понятно, если перерисовать нашу последовательную цепь таким образом, чтобы все ее компоненты находились на одной линии:

Перед вами все та же последовательная цепь, только ее компоненты расположены иным способом. Обратите внимание на полярность напряжений резисторов относительно батареи: напряжение последней отрицательно слева и положительно справа, тогда как напряжения на всех резисторах ориентированы в другую сторону (положительны слева и отрицательны справа). Различия в полярности обусловлены тем, что резисторы сопротивляются потоку электронов, производимому батареей.

На следующем рисунке вы можете увидеть показания цифровых вольтметров на каждом компоненте этой цепи:

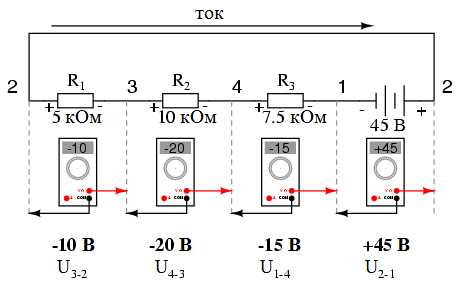
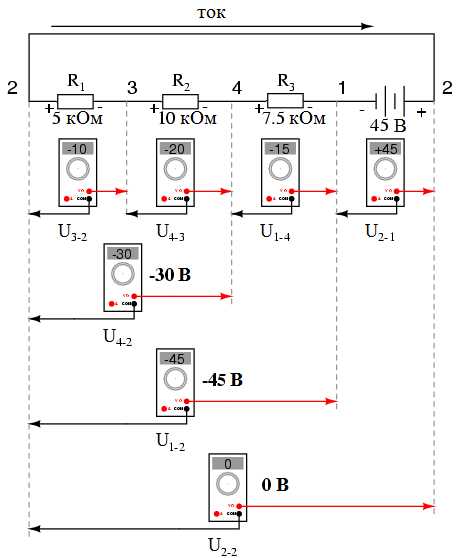
Если мы произведем замеры напряжения на группах компонентов, начиная с левой стороны цепи (с резистора R1), то увидим, что напряжения складываются алгебраически (к нулевому результату):

То, что напряжения последовательной цепи складываются, является очевидным фактом, и в этом сложении очень важную роль играет полярность напряжения. Измеряя напряжение на резисторах R1, R1--R2, R1--R2--R3 (символ двойного тире "--" используется для того, чтобы показать последовательное соединение между резисторами R1, R2, и R3) мы видим, что его величина (хоть и отрицательная) последовательно увеличивается от начальной точки к каждому последующему резистору. Такое увеличение является следствием одинаковой ориентации (полярности) напряжения на всех резисторах ("+" слева, "-" справа). Сумма напряжений на резисторах R1, R2, и R3 нашей схемы будет равна 45 вольт, что аналогично напряжению на выводах батареи, за тем исключением, что полярность батареи ("-" слева, "+" справа) противоположна полярности суммарного напряжения резисторов. Таким образом, общее напряжение на всей линейке компонентов схемы будет равно нулю (45В + (-45В) = 0).

Полученное в результате суммирования итоговое напряжение, величиной 0 вольт, вполне закономерно. Посмотрев на схему можно увидеть, что ее крайняя левая точка (точка № 2 слева от резистора R1) непосредственно связана с крайней правой точкой (точкой № 2 справа от батареи). Поскольку непосредственно связанные точки являются электрически общими по отношению друг к другу, напряжение между ними должно быть равно нулю.

Второй закон Кирхгофа будет работать не только на последовательной конфигурации цепи, но и на любой другой. Посмотрите как он работает на следующей параллельной цепи:

В параллельной цепи, как вы знаете, напряжение на каждом резисторе равно напряжению батареи, которое в нашем случае составляет 6 вольт. Подсчитав напряжение в последовательности точек 2-3-4-5-6-7-2, мы получим:

Обратите внимание, суммарное напряжение мы обозначили как U2-2. А обозначили мы его так из за того, что начали измерения в точке 2, и закончили в этой же точке. Алгебраическая сумма напряжений в этом случае будет равна напряжению между точками 2-2, которое конечно-же равно нулю.

Тот факт, что эта цепь параллельная а не последовательная, никак не влияет на справедливость второго закона Кирхгофа. Любая схема вообще может быть "черным ящиком", а ее конфигурация может быть полностью скрыта от нашего взгляда. При этом, если контрольные точки этой схемы будут открыты, то замеры напряжения между ними подтвердят верность данного закона:

Попробуйте в вышеприведенной схеме измерить напряжения любой последовательностью шагов между любыми ее точками (возвращаясь при этом в исходную точку), и вы увидите, что алгебраическая сумма напряжений всегда равна нулю.

Последовательность точек, к которой можно применить закон, не обязательно должна соответствовать реальному потоку электронов. Единственным условием, которое необходимо выполнить, является то, что последовательность должна начинаться и заканчиваться в одной точке цепи, при этом полярность при проведении замеров должна неукоснительно соблюдаться. Давайте рассмотрим абсурдный пример, замерив напряжения в последовательности точек 2-3-6-3-2 этой же цепи:

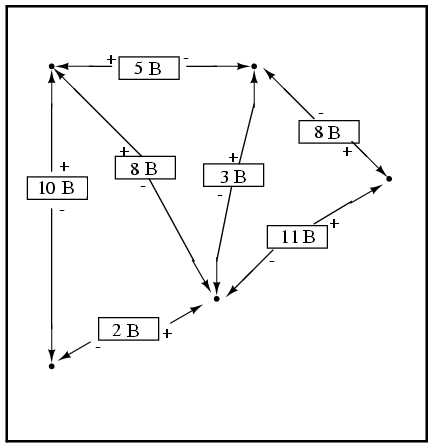
Второй закон Кирхгофа можно использовать для определения неизвестного напряжения сложной цепи, в которой остальные напряжения выбранной последовательности точек известны. Возьмем в качестве примера следующую сложную цепь (представляющую две последовательные цепи, основания которых соединены проводом):

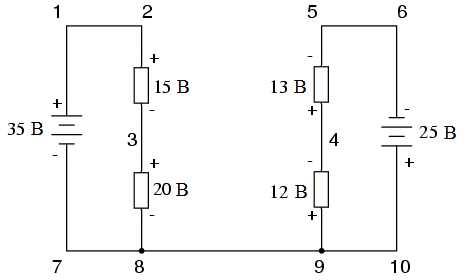
Для упрощения задачи мы опустим значения сопротивлений, оставив только значения напряжений на каждом резисторе. Так как две изображенные на рисунке последовательные схемы имеют общий провод (провод 7-8-9-10), у нас появляется возможность измерить между ними напряжение. Если мы хотим определить напряжение между точками 4 и 3, то его нужно подставить в уравнение Второго закона Кирхгофа как неизвестное:

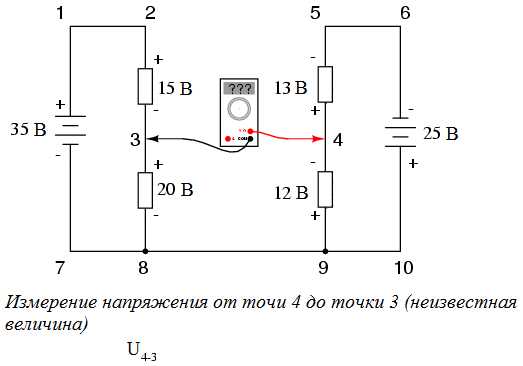
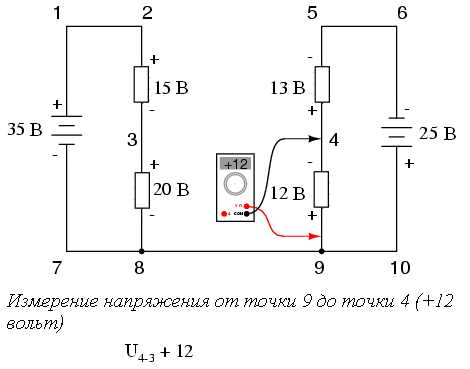
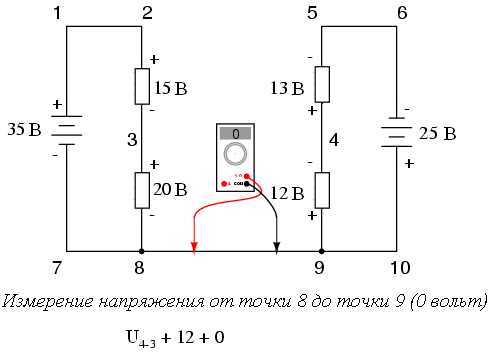
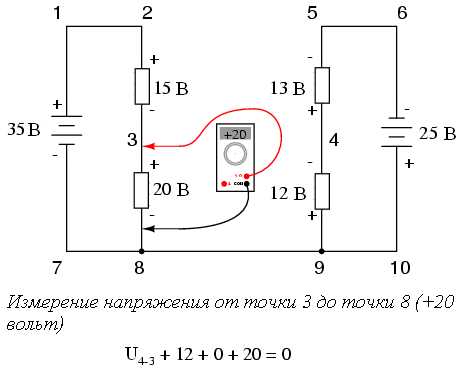
В ходе измерения напряжений в последовательности точек 3-4-9-8-3 мы записывали числа так, как их отображал цифровой вольтметр. При этом красный щуп прибора подсоединялся к первой точке, а черный - ко второй. Таким образом, напряжение от точки 9 до точки 4 оказалось положительным +12 вольт, так как красный щуп подключался к точке 9, а черный - к точке 4. Напряжение от точки 3 до точки 8 так же положительно + 20 вольт (красный щуп к точке 3, черный - к точке 8). И напряжение от точки 8 до точки 9 имеет нулевое значение, потому что эти две точки являются электрически общими.

Итак, окончательным ответом для напряжения от точки 4 до точки 3 будет -32 вольта. Именно такое напряжение покажет вольтметр, если мы подключим его красный щуп к точке 4, а черный - к точке 3:

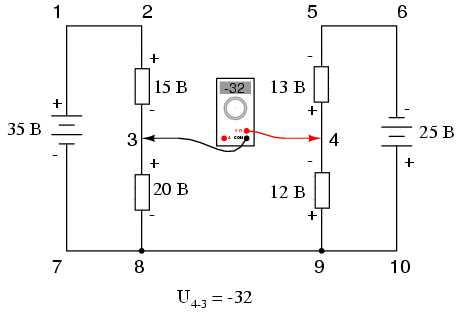
Если бы наше уравнение начиналось с U3-4 вместо U4-3, то последовательность измерений проводилась бы при противоположной ориентации тестовых проводов мультиметра. В этом случае окончательный ответ был бы следующим - U3-4=+32 В:

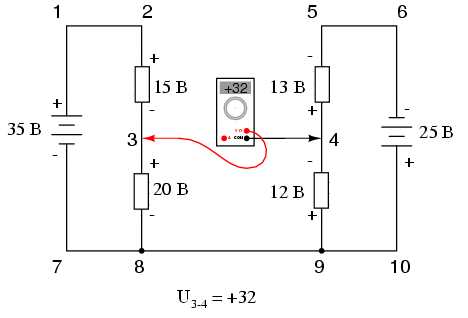
Здесь важно понять, что оба подхода являются правильными. В обоих случаях мы достигаем правильной оценки напряжения между точками 3 и 4.

www.radiomexanik.spb.ru

Первый закон Кирхгофа: определение, формулы, физический смысл

Первый закон Кирхгофа основан на принципе непрерывности и применим к узлу электроцепи.

Первый закон Кирхгофа определяет взаимосвязь между суммой токов, сходящихся в одном узле, и формулируется следующим образом:

Алгебраическая сумма величин токов Ik, сходящихся в любой точке (узле) электроцепи, равна нулю в любой момент времени

∑ Ik = 0,

при этом k — количество ветвей, сходящихся в узле цепи;

Ik – мгновенная величина тока для k-й ветви.

Физически Первый закона Кирхгофа означает: движение электрических зарядов осуществляется таким образом, что ни в одном из участков цепи он не имеет тенденцию к накоплению.

Отсюда, вытекает еще одна формулировка закона: в любом узле электроцепи сумма токов направленных к узлу оказывается равной сумме токов, направленных от этого узла, или:

∑ Ik = ∑ Im,

при этом k — количество ветвей, втекающих в узел;

m- — количество ветвей, вытекающих из узла.

Узлом электрической цепи принято называть точку подключения 3-х и более ветвей. ток принимается со знаком «+», если он втекает в узел, и со знаком «-», если вытекает.

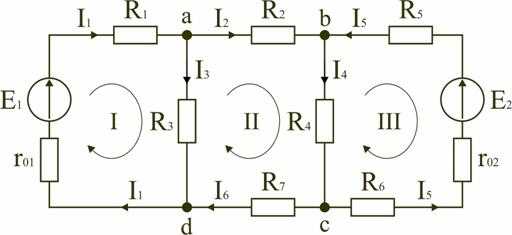
К примеру, рассмотрим баланс токов на примере схемы:

I1 + I2 + I3 – I4 – I5 = 0, либо

I1 + I2 + I3 = I4 + I5.

Очевидным фактом, является то, что формулировка формы записи может иметь различный характер. Существенным является лишь принимаемая договоренность о знаке токов: нельзя использовать разнонаправленное направление в пределах одной электрической цепи для одного или нескольких узлов.

Направление тока для каждой цепи определяют произвольно. При этом нет необходимости стремиться, чтобы для всех узлов использовались токи различных направлений. Также может иметь место ситуация, что в каком-то узле все токи будут направлены от узла или к нему, что тем самым нарушает принцип непрерывности. Но в такой ситуации в процессе определения значений токов один или несколько будут отрицательными, что будет служить признаком об их протекании в противоположном направлении от принятого.

При расчете разветвленных электроцепей используются второй закон Кирхгофа. Они были сформулированы в 1945г. великим физиком 19 в. Густавом Робертом Кирхгофом.

pue8.ru

Каждый закон Кирхгофа прост и понятен :: SYL.ru

Густав-Роберт Киргоф, выдающийся немецкий физик и математик позапрошлого века, открыл и сформулировал два электротехнических закона, названных в его честь.

Открытия Кирхгоффа

При всей видимой простоте и понятности, законы Кирхгофа стали фундаментальными основами современной науки и базой для методов схематических расчетов. Их практическое значение трудно переоценить. Базой для научных изысканий профессора Кирхгофа стали законы сохранения заряда и энергии, открытые ранее. Некоторые специалисты считают, что правильнее называть описанные Кирхгоффом закономерности правилами, чтобы не путать их с другими замечательными открытиями этого физика, касающимися способностей тел излучать и поглощать энергию, а также зависимости скорости протекания химических реакций от температуры. Однако в научной и технической литературе принято все же пользоваться термином «закон Кирхгофа», тем самым подчеркивая заслуги этого великого ученого в области электротехники. Итак, их два.

1. Закон Кирхгофа о токах в узлах

Узлами в электротехнике называют точки соединения проводников в количестве не менее трех. Для того чтобы понять действие Первого закона Киргофа, достаточно представить себе обычный водопроводный тройник. Если в одну из труб подается вода, то в две остальные она вытекает. Возможен и другой вариант, когда отводная труба одна, а приточных две, но в любом случае, сколько воды в тройник затечет, столько же и вытечет. Теперь задачу можно усложнить, допустив, что количество входов и выходов в узле сколь угодно большое. Однако результат будет тот же, количество поступающей и уходящей жидкости будет равным, то есть, говоря языком математики, алгебраическая сумма расходов равна нулю. Первый закон Кирхгофа рассматривает электрические токи в узлах, которые ведут себя так же, как и вода в тройнике. Если есть входящие и выходящие токи, то их сумма с учетом знака будет нулевой. При этом величина входящих токов обозначается положительным знаком «плюс», а выходящих – отрицательным «минус». Математическая формула выглядит примерно так:

∑(I вх., … I вых.) = 0

где I вх. - величины входящих токов со знаком «+»;

I вых. - величины выходящих токов со знаком «-».

2. Закон Кирхгофа о сумме падений напряжений

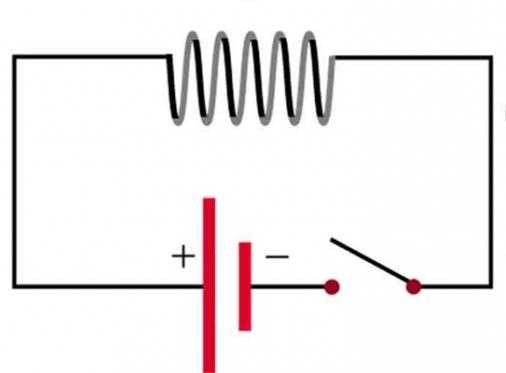
Второй закон Кирхгофа понять несколько сложнее, у него нет столь прямых и наглядных ассоциаций как у первого, тем не менее, он тоже несложен. Для начала следует представить себе замкнутую простейшую электрическую цепь, состоящую из источника питания и активной нагрузки в виде сопротивления. При замыкании клемм выключателя через резистор пойдет ток, и все подаваемое напряжение на нем же упадет. Задача вновь усложняется, и количество сопротивлений изменяется. Теперь их много, и у всех разная величина. При прохождении через них электрического тока он будет в цепи одинаковым и, согласно закону Ома, равен напряжению источника, поделенному на сумму всех сопротивлений. На каждом из них будет падать его часть. Так вот, Второй закон Кирхгофа гласит, что общая сумма падений напряжений на каждом из участков цепи равна величине напряжения питания. Говоря иными словами, общая алгебраическая сумма вместе с источником равна нулю.

Простейшая математическая формула описывает Второй закон Кирхгофа следующим образом:

∑U ц = 0

где U ц – падения напряжений на разных участках замкнутой электрической цепи (контура).

www.syl.ru

Закон Кирхгофа в элекротехнике

В расчетах электрических цепей переменного и постоянного тока кроме знаменитой формулы Ома также применяется закон Кирхгофа. Человек, работа которого связана с электротехникой, должен даже среди ночи без запинки дать определения для каждого из двух законов. Часто это необходимо не столько для выполнения расчетов, сколько для понимания происходящих процессов.

В далеком 1845 году германский физик Густав Кирхгоф на основании трудов Максвелла (сохранение заряда и свойства электростатического поля) сформулировал два Правила, позволяющие указать соотношение между током и напряжением в замкнутой электрической цепи. Благодаря этому стало возможно решать практически любые прикладные задачи, связанные с электричеством. Закон Кирхгофа, используемый для расчета линейной электрической цепи, дает возможность получить классическую систему линейных уравнений, учитывающих напряжения и токи, которые становятся известными после решения поставленной задачи.

Формулировка предполагает использование терминов электрических «контур, узел и ветвь». Ветвь – это любой двухсторонний участок цепи, произвольный ее отрезок. Контур – это система зацикленных ветвей, то есть, начав мысленное движение из произвольной точки по любой ветви, в итоге все равно попадешь в место, откуда движение началось. Более понятно ветви называть «закольцованными», хотя это не совсем корректно. Узел – это точка, в которой сходятся две или более ветвей.

1 закон Кирхгофа очень прост. Он основывается на фундаментальном законе сохранения заряда. Первый закон Кирхгофа гласит: сумма токов (алгебраическая), стекающихся по ветвям к единому узлу, равна нулю. То есть, I1+I2+I3=0. Для расчетов принято считать, что значение втекающих в узел токов имеет знак «+», а вытекающих «-». Поэтому расширенная формула приобретает вид I1 + I2 - I3 = 0. Другими словами: количество втекающего в узел тока равно количеству вытекающего. Этот закон Кирхгофа очень важен для понимания принципов работы электрооборудования. Например, он поясняет, почему при соединении обмоток электрического двигателя по схеме «звезда» или «треугольник» не происходит межфазного короткого замыкания.

2 закон Кирхгофа обычно используют для расчета замкнутого контура с определенным количеством ветвей. Он непосредственно взаимосвязан с третьим законом Максвелла (неизменное магнитное поле). Правило гласит, что алгебраическая сумма падений напряжений на каждой из веток контура приравнивается к сумме значений ЭДС для всех ветвей рассчитываемого контура. Очевидно, что при отсутствии в замкнутой цепи источников электрической энергии (ЭДС), итоговое падение напряжений также будет равняться нулю. Говоря более простым языком, энергия источника лишь преобразуется на потребителях, а при возвращении стремится к своему исходному значению. Использование данного закона имеет ряд особенностей, как и в случае с первым.

Составляя уравнение цепи, принято считать, что численное значение ЭДС имеет положительный знак, если изначально принятое направление обхода контура (обычно по часовой стрелке) совпадает с ее направлением, и отрицательное, если направления противоположны. То же самое касается резисторов: если направление движения тока такое же, как у выбранного обхода, то падению напряжения на нем приписывается знак «+». Например, E1 - E2 + E3 = I1R1 - I2R2 + I3R3 + I4R4…

В результате обхода всех ветвей, входящих в контур, составляется система линейных уравнений, решив которую, удается узнать все токи ветвей (и узлов). Решаются полученные соотношения с помощью метода контурных токов.

Сложно переоценить значение законов Кирхгофа для электротехники. Простота написания формул и их решение с помощью способов классической алгебры явились причиной для широкого их использования.

fb.ru

Законы Кирхгофа - это... Что такое Законы Кирхгофа?

Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.

Формулировка

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений для переменных напряжений

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример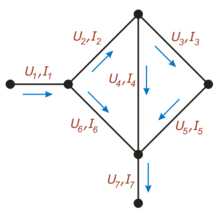

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

Особенности составления уравнений для расчёта токов

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме;
- положительные направления обхода контуров для составления уравнений по второму закону.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.[источник не указан 912 дней]

Закон излучения

Закон излучения Кирхгофа — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Примечания

Литература

Матвеев А. Н. Электричество и магнетизм — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи — 11-е издание. — М.: Гардарики, 2007.

biograf.academic.ru