Законы Кирхгофа для цепей синусоидального тока. Второй закон кирхгофа для цепи

Второй закон Кирхгофа. Второе правило Киргофа для расчета цепей постоянного тока

Второй закон Кирхгофа

Алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре.
Алгебраическая сумма падений напряжений в замкнутом контуре равна сумме действующих ЭДС в этом контуре. Если в контуре нет источников электродвижущей силы, то суммарное падение напряжений равно нулю.
Алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю.
Алгебраическая сумма падений напряжений на пассивных элементах равна алгебраической сумме ЭДС и напряжений источников тока, действующих в этом контуре.

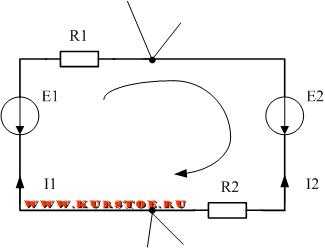
Т.е. падение напряжения на R1 со своим знаком плюс падение напряжения на R2 со своим знаком равно напряжение источника эдс 1 со своим знаком плюс напряжение на источнике электродвижущей силы 2 со своим знаком. Алгоритм расстановки знаков в уравнениях по закону Кирхгофа описан на отдельной странице.

Уравнение для второго закона Кирхгофа

Составлять уравнения по второму закону Кирхгофа можно разными способами. Самым удобным считается первая формула.

Так же можно уравнения писать в таком виде.

Физический смысл второго закона Кирхгофа

Второй закон устанавливает связь между падением напряжения на замкнутом участке электрической цепи и действием источников ЭДС на этом же замкнутом участке. Он связан с понятием работы по переносу электрического заряда. Если перемещение заряда выполняется по замкнутому контуру, возвращаясь в ту же точку, то совершенная работа равна нулю. Иначе бы не выполнялся закон сохранения энергии. Это важное свойство потенциального электрического поля описывает 2 закон Кирхгофа для электрической цепи.

www.kurstoe.ru

Второй закон Кирхгофа — третий кит электротехники

Удивительно не то, как просто всё рассчитывается, когда знаешь два понятных всем правила расчёта — первый и второй Законы Кирхгофа, а то, как гениально это было придумано.

Ведь не было тогда бытовой электрической сети. Куда просто вкрутил лампочку, нажал выключатель, и всё — заработало напряжение, побежал ток, разогрелась спираль лампочки и засиял свет. Вот она, понятная работа электричества. Её нам сейчас ничуть не труднее осознать, чем бурчание воды в отоплении или гудение воздуха в инструменте трубача.

Закон Ома — первый кит электротехники

А когда Георг Симон Ом, изучая гальванические, как тогда называли, цепи, вывел своё простейшее соотношение, этого понять не мог никто, кроме немногих посвящённых. Просто потому, что обыденный мозг тогда сразу упирался в нечто невообразимое, а значит, непреодолимое: что это за течение такое, ток частиц, которых не то что пощупать, но и представить нельзя ввиду абсолютно исчезающей малости. Да ещё «текущих» в металле, твёрдом предмете. Уж не то, что попытаться составлять какие-либо точные формулы.

Теперь это соотношение кажется простым и ясным, как удар молнии. Видимо, он сумел почувствовать это явление — электрическое напряжение. Если цепь разомкнута, то тока ещё никакого нет, ничего не нагревается и не пузырится (как вода под током), а напряжение вот оно — попробуй, тронь! Видимо, как-то сумел гений потрогать и попробовать.

Собственно, вся любая электрическая цепь и описана законом Ома. Источник, дающий напряжение и нагрузка, подставляющая напряжению своё тело, отчего получается электрический ток. Соотношение простейшее — чем больше напряжение, тем больше ток. А конкретно каким он получится, определяет пропускная способность нагрузки, G, или проводимость.

I=U*G

Удобнее и нагляднее оказалось вместо проводимости пользоваться понятием сопротивления, R, величиной обратной проводимости (R=1/G).

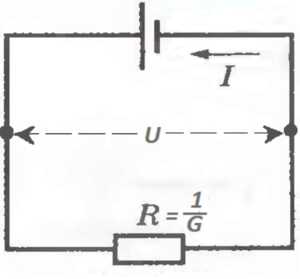
И обозначения на первой электросхеме самые простейшие: прямоугольничек — нагрузка, две линии поперёк тока — батарейка.

Самая первая электрическая схема

Видимо, и подключали поначалу что-то одно к чему-то одному. Но вот и эта схема «под напором реальности» усложняется. Во-первых, сама батарейка имеет сопротивление.

Как это изобразить, вот так?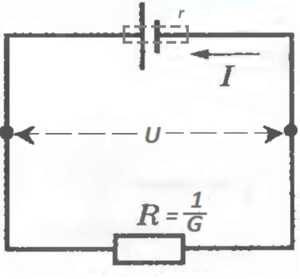

Некрасиво.

Лучше располагать рядом так:

Есть искушение поставить этот прямоугольничек на другую сторону, рядом с нагрузкой, а нельзя, всё-таки батарейка и её внутреннее сопротивление — одно нераздельное физическое устройство.

Чтобы видеть действие тока, лучше в качестве нагрузки использовать лампочку. Понятно, с выключателем.

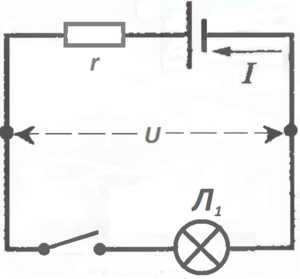
Мы получили последовательную цепочку.

Ток во всех её частях обязан быть одним и тем же, то есть одинаковый везде.

Это логично, и если включить выключатель, лампочка сразу загорится.

При этом никто и не задумывается, что если у нас через лампочку течёт ток всего в один ампер, то это значит, что каждую секунду через неё пробегает:

6 квинтиллионов 241 квадриллион 509 триллионов 125 миллиардов 493 миллиона 690 тысяч с небольшим электронов.

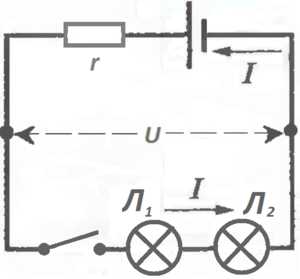
И все они вышли из небольшой батареечки и в неё же и вернутся с другой стороны.

Если поставить вместо одной лампочки две одинаковых, то они загорятся вполнакала, то есть ток I, протекающей последовательно из батарейки через выключатель сначала в лампочку Л1, потом в лампочку Л2 и снова в батарейку, станет меньше, чем был, когда стояла одна лампочка.

Это значит, что сопротивление стало больше: было R у одной лампочки, стало R+R, то есть 2R.

Токи и напряжения в сети

Точную величину тока можно подсчитать, если применить закон Ома ко всей нашей цепи, общее сопротивление которой есть сумма сопротивлений всех её нагрузок.

(1) А если оставить в формуле сопротивление только одной лампочки, то, зная, что ток у нас везде один и тот же, можно вычислить напряжение Uл конкретно для этого потребителя, лампочки.

Это напряжение, которое падает именно на нашу лампочку, так и называется «падение напряжения». Оно примерно вдвое меньше нашего напряжения питания U. Примерно — потому что в формуле (1) среди сопротивлений есть ещё небольшой довесок в виде r, внутреннего сопротивления нашей батареи. Что делать, она не идеальна, и вместе со всеми остальными потребляет энергию (свою же собственную) и даже греется от этого. Хотя сопротивление её достаточно малое.

А теперь взглянем на нашу цепь как на единый контур, который можно обходить по часовой или против часовой стрелки. Ток наш идёт, как нарисовано, против часовой стрелки. Двинемся по этому направлению с любого места и пройдём всё, складываем падения напряжения на всех попадающихся по дороге приборах.

Для токов — узлы, для напряжений — контуры

Получится:

Последним напряжением добавлено то, которое вырабатывается батареей, только со знаком минус, так как оно работает не на потребление, а наоборот, вырабатывается и поставляется в сеть нашей героической батареей. И что у нас получилось?

Правило Кирхгофа для напряжений (2й закон)

А получилось ровно 0. Потому что вся энергия от батареи потребляется лампочками + внутреннее сопротивление батареи. И понятно, это есть высшая справедливость природы. То есть второй закон Кирхгофа в действии.

И вдруг у нас случился… прорыв.

Правило Кирхгофа для токов (1й закон)

К нам в двух точках — А и B — подключились неизвестные, скорее всего, инопланетяне.

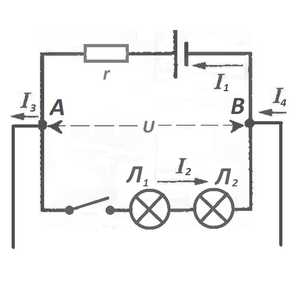
И начали качать от нас энергию. И теперь мы знаем, что ток I3 и ток I4 — не наши, они инопланетянские. И наша схема может быть безнадёжно испорчена.

Но!

А обойдём ка мы контур снова. Может быть, не всё ещё потеряно. И вот:

Ur=I1*r

Uл1=I2*R=Uл2

И, наконец:

U=Uг+Uл1+Uл2.

Потому что I1=I2+I3. И I1=I2+I4.

То есть сколько току вытекло в качестве тока I3 в точке А, столько его и вернулось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А помогло нам при этом здравое рассуждение, о том, что в любой точке цепи, где электрическая сеть разветвляется, общее количество тока, вытекающего из узла, то есть этой точки, равно количеству тока, втекающего в этот узел. Поэтому смело рисуем схему, зная, что нам помог уже первый, а не второй закон Кирхгофа:

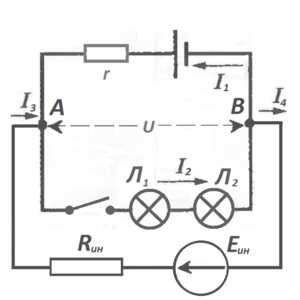Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.

Ох уж эти выдумки инопланетянские! С нашей стороны осталось только в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин) в противоположное направление. Потому что мы сначала подумали, что инопланетяне плохие, а они оказались хорошими.

Расчёт цепи по законам Кирхгофа интуитивно понятен — правила позволяют рассчитывать электрические цепи, то есть определять все неизвестные параметры — токи, напряжения — любой, сколь угодно замысловатой цепи.

Применение законов Кирхгофа для расчёта сложных цепей

Цепь состоит из ветвей, соединяющихся в узлах. Ветвь — это несколько последовательно соединённых электрических приборов. В узлах могут соединяться три и более ветвей. Это значит, что через узел проходят токи, выходящие из ветвей, которые в нём соединяются.

Ну и теперь, вооружившись проверенными нами базовыми законами электротехники, решим пример, зная, что всё и для любой электрической цепи решаемо.

Смело решаем задачу.

Путь таков:

Составляются уравнения для токов в узлах — работает первый закон Кирхгофа. Составляются уравнения для падений напряжений по всем независимым контурам — дело второго закона Кирхгофа.
Уравнения сводятся в систему и решаются методами математики для системы из N линейных уравнений с N неизвестными.
Делается проверка решения другим способом, например, подсчётом общей мощности сети

Составляем уравнения для токов, втекающих/вытекающих в узлы. Узлов сего три, значит, уравнений будет 3-1, то есть два.

Теперь составляем уравнения для контуров и падений напряжения в них. Контуров у нас независимых три (в которых в каждом есть хотя бы одна ветвь, не встречающаяся в других).

Вот и получается три уравнения по второму закону Кирхгофа: Собрав все пять уравнений вместе, получаем систему из пяти уравнений с пятью неизвестными.

Остальное — дело королевы наук, то есть математики. Такие системы она щёлкает не глядя.

И получаются вполне похожие на правду ответы:

А мы знаем, хорош тот ответ, который поддаётся проверке.

Сделаем-ка мы расчёт мощности, выделяемой на всех устройствах данной схемы при полученной нами картине токов и напряжений двумя способами, пользуясь немного разными определениями для мощности:

мощность как произведение тока на напряжение
мощность, как квадрат силы тока, умноженный на сопротивление

Как видим, всё у нас правильно, задача нашего непростого примера решена.

instrument.guru

Законы Кирхгофа для цепей синусоидального тока — КиберПедия

Математическая формулировка двух законов Кирхгофа для цепей синусоидального тока зависит от выбранного представления синусоидальных величин. Будем далее пользоваться для аналитического представления синусоидальных величин тригонометрическими функциями и соответствующими им комплексными значениями. При тригонометрической форме представления законы Кирхгофа определяют зависимость между мгновенными значениями соответствующих синусоидальных величин. При втором виде представления законы Кирхгофа определяют зависимость между комплексными значениями соответствующих синусоидальных величин.

Первый закон Кирхгофа.

По первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю. Для цепей синусоидального тока это означает, что в ветвях, сходящихся в любом узле, алгебраическая сумма мгновенных значений токов равна нулю:

или

где n – число ветвей, сходящихся в узле.

Принято соглашение о том, что все синусоидальные токи, положительные направления которых выбраны к узлу (от узла), записываются со знаком плюс (минус).

Положим

Тогда по первому закону Кирхгофа

для любого момента времени.

Чтобы получить математическую формулировку первого закона Кирхгофа в комплексной форме, представим все синусоидальные токи соответствующими им комплексными значениями. Тогда первый закон Кирхгофа запишется следующим образом:

то есть алгебраическая сумма комплексных значений тока всех ветвей, сходящихся в каком-либо узле электрической цепи, равна нулю.

Векторная диаграмма токов:

Второй закон Кирхгофа.

По второму закону Кирхгофа алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах (пассивные элементы) в любом контуре электрической цепи в каждый момент времени равна алгебраической сумме ЭДС этого контура. В цепях синусоидального тока значения напряжений на пассивных элементах любого контура непрерывно изменяются, но, тем не менее, алгебраические суммы мгновенных значений напряжений и ЭДС одинаковы:

или

где n – количество пассивных элементов в контуре, m – количество источников ЭДС в контуре. Будем считать, что все синусоидальные напряжения uk и ЭДС ek, для которых положительные направления совпадают с произвольно выбранным направлением обхода контура, записываются со знаком плюс и в противном случае со знаком минус.

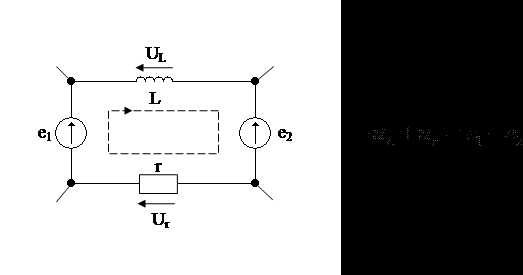
Чтобы получить математическую формулировку второго закона Кирхгофа в комплексной форме, представим все синусоидальные напряжения и ЭДС соответствующими комплексными значениями.

Второй закон Кирхгофа в комплексной форме записывается:

то есть алгебраическая сумма комплексных значений напряжений на всех пассивных элементах какого-либо контура электрической цепи равна алгебраической сумме комплексных значений всех ЭДС этого контура. В этом случае комплексные значения напряжений и ЭДС положительны, если совпадают с произвольно выбранным направлением обхода контура.

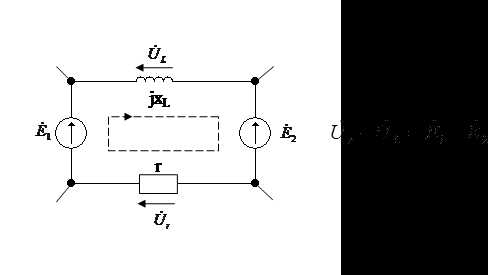
Векторная диаграмма ЭДС и напряжений:

cyberpedia.su

Законы Кирхгофа для электрических цепей. — КиберПедия

Законы Кирхгофа для электрических цепей.

Первый закон Кирхгофа.

Первый закон Кирхгофа показывает связь токов и узлов электрической цепи.

Сумма токов всех ветвей, которые сходятся в один узел электроцепи, равняется нулю.

Второй закон Кирхгофа.

Второй закон Кирхгофа описывает алгебраическую зависимость между электродинамической силой и напряжением в замкнутой электроцепи.

В любом замкнутом контуре сумма электродинамической силы равна сумме падания напряжения на сопротивлениях, относящихся к данному контуру.

Для написания формул, определяющих второй закон Кирхгофа, берут положительное значение электродинамической силы и падение напряжений, если направление на относящихся к ним отрезках контура совпадает с произвольным направлением обхода контура. А если же направление электродинамической силы и токов противоположны выбранному направлению, то эти электродинамические силы и падение напряжений берут отрицательными:

Алгоритм определения знака величины электродинамической силы и падения напряжений:

1.Выбираем направление обхода контурных цепей. Тут возможны несколько вариантов: либо по часовой стрелке, либо против часовой стрелки.

Произвольным образом выбираем направление движения токов протекающих через элементы контурных цепей.

3.Расставляем знаки для электродинамической силы и падения напряжений (не забывая о совпадении или несовпадении направления электродинамической силы с направлением движения обхода контура).

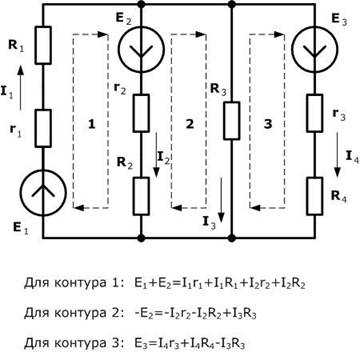
Расчет простых цепей при различных схемах соединения потребителей.

Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры.

Существует последовательное и параллельное соединение потребителей.

Последовательное соединение (в) — это такое соединение, при котором все потребители включены один за другим в одну линию. Поэтому по всем потребителям проходит ток одинаковой силы.

I = U/R = 12 В / З Ом = 4 А

Общее сопротивление внешней цепи равно сумме сопротивлений всех включенных потребителей.

R = R1 + R2 = 1 Ом + 2 Ом = 3 Ом

При параллельном соединении (г) к одной точке цепи подключают по одному выводу каждого потребителя, а к другой точке цепи другие выводы. В нашем примере внешняя цепь имеет два разветвления, т. е. две параллельные ветви. Оба потребителя R1 и R2 находятся под одинаковым напряжением U = 12 В.

Сила тока в цепи каждого потребителя зависит от величины его сопротивления:

В цепи первого потребителя I1 = U/R1 = 12 В / 1 Ом = 12 А

В цепи второго потребителя I2 = U/R2 = 12 В / 2 Ом = 6 А

Общая сила тока во внешней цепи равна сумме сил токов в цепях всех параллельно включенных потребителей:

I = I1 +I2 = 12+6 = 18 А

Методы расчета сложных электрических цепей.

Выбирают положительные направления токов в ветвях электрической цепи.

Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.

3) Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов ветвей можно использовать одиночные цифры.

Порядок расчета

Выбираются независимые контуры, и задаются произвольные направления контурных токов.В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях:

(4)

(5)

Суммарное сопротивление данного контура называется собственным сопротивлением контура.Собственные сопротивления контуров схемы:

, .

Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров:

где R12 - общее сопротивление между первым и вторым контурами;R21 - общее сопротивление между вторым и первым контурами.E11 = E1 и E22 = E2 - контурные ЭДС.В общем виде уравнения ( 4 ) и ( 5 ) записываются следующим образом:

Собственные сопротивления всегда имеют знак "плюс".Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению. Решая уравнения ( 4 ) и ( 5 ) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях. Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

Магнитная цепь и ее расчет.

Магнитная цепь (МЦ) — это устройство из ферромагнитных сердечников с воздушными зазорами или без них, по которым замыкается магнитный поток. Применение ферромагнетиков имеет целью получение наименьшего магнитного сопротивления, при котором требуется наименьшая МДС для получения нужной магнитной индукции или магнитного потока.

Простейшая магнитная цепь — это сердечник кольцевой катушки. Применяются магнитные цепи неразветвленные и разветвленные, отдельные участки которых выполняются из одного или из разных материалов. Расчет магнитной цепи сводится к определению МДС по заданному магнитному потоку, размерам цепи и ее материалам. Для расчета цепь делят на участкиl1, l2и т. д. с одинаковым сечением по всей длине участка, т. е. с однородным полем, определяют магнитную индукциюВ= на каждом из них и по кривым намагничивания находят соответствующие напряженности магнитного поля. Магнитная цепь (MЦ) состоит из двух основных элементов: - источника магнитной энергии; - магнитопровода.

Источник магнитной энергии в реальных МЦ бывает двух видов:

- постоянный магнит; - электромагнит.

Пример расчета неразветвленных магнитных цепей.

Рассмотрим расчет магнитной цепи, размеры и и материалы которой, а также количество и расположение обмоток с токами известны. Расчет проводится с использованием закона полного тока. Такой расчет предусматривает решение одной из двух задач: прямой задачи и обратной задачи.

Прямая задачарасчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Если одна из величин I или W задана, то определяется только другая величина.

Законы Кирхгофа для электрических цепей.

Первый закон Кирхгофа.

cyberpedia.su

Законы Кирхгофа - это... Что такое Законы Кирхгофа?

Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.

Формулировка

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений для переменных напряжений

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример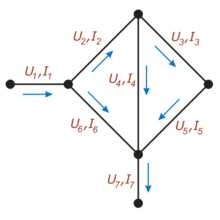

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

Особенности составления уравнений для расчёта токов

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме;
- положительные направления обхода контуров для составления уравнений по второму закону.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.[источник не указан 912 дней]

Закон излучения

Закон излучения Кирхгофа — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Примечания

Литература

Матвеев А. Н. Электричество и магнетизм — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи — 11-е издание. — М.: Гардарики, 2007.

dic.academic.ru

§ 10. Законы Кирхгофа

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значения токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

Первый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

?I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А (рис. 23, а)

I1 + I2 + I3 – I4 – I5 = 0 (17)

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах (рис. 23, б).Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

?E = ?IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2

(рис. 24, а), внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,получим:

E1 – E2 = IR01 + IR02 + IR1 + IR

При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной.Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можнорассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарееЕсли же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В неко-

Рис 24. Схемы электрических цепей с несколькими источниками и приемниками электрической энергии: а и б — неразветвленных; в — разветвленной

торых случаях такое включение недопустимо, так как ток в цепи резко возрастает.Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

electrono.ru

1.2. Законы Кирхгофа

Первый закон Кирхгофа: алгебраическая сумма всех токов, втекающих в любой узел, равна нулю. Токи, втекающие в узел, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот). Если, например, в узел втекает ток II, а вытекают токи 12 и 13, то первый закон Кирхгофа может быть записан в виде выражения: 11-12-13=0.

Второй закон Кирхгофа: алгебраическая сумма ЭДС любого замкнутого контура равна алгебраической сумме падений напряжений на всех участках контура.

При применении второго закона Кирхгофа необходимо учитывать знаки ЭДС и выбранное направление токов на всех участках контура. Направление обхода контура выбирается произвольным; при записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода независимо от направления протекающего через них тока, принимаются положительными, а ЭДС обратного направления принимаются отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех участках, в которых положительное направление тока совпадает с направлением обхода независимо от направления ЭДС на этих участках, и со знаком минус — на участках, в которых положительное направление тока противоположно направлению обхода.

Общая методика применения законов Кирхгофа для расчета сложных многоконтурных цепей такова. Устанавливается число неизвестных токов, которое равно числу ветвей р. Для каждой ветви задается положительное направление тока. Число независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов q (точек соединения не менее чем трех проводников) минус единица, т.е.д-1. Число независимых уравнений, составляемых по второму закону Кирхгофа, равно числу контуров n=p-q+\. Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов р. Решение этой системы уравнений и дает значения искомых токов.

Для иллюстрации изложенной методики рассмотрим многоконтурную цепь постоянного тока на рис. 5.4. В этой цепи всего три узла: А, В и С (q =3), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. При числе ветвей цепи р=5 число контуров п=5-3+1=3, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, будет равно числу неизвестных токов в пяти ветвях схемы.

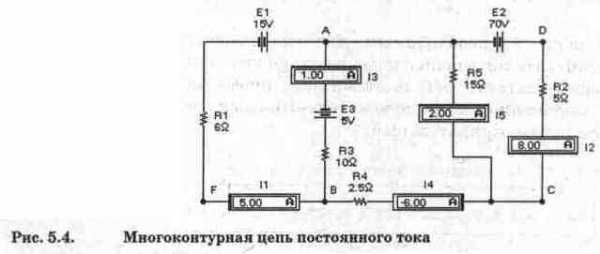
Выберем положительные направления токов, которые на схеме обозначены соответствующим включением амперметров. Например, ток II течет справа налево и втекает в узел А (положительное направление тока), поскольку отрицательная клемма, отмеченная утолщенной черной линией, находится слева и ток через амперметр будет течь справа налеро. Ток 12 вытекает из узла А, поскольку ток через одноименный амперметр будет течь сверху вниз (к отрицательному зажиму, расположенному на нижней грани иконки) и т.д.

Составим систему уравнений Кирхгофа:

для узла А 11-12+13-15=0;

для узла В -11-13-14=0;

для контура ABFA E1+E2=I1-R1-I3-R3;

для контура АВСА E3=-I3-R3+I4-R4+I5-R5;

для контура ADCA E2=I2-R2+I5-R5.

После подстановки в полученные уравнения числовых значений они приобретают следующий вид:

11-12+13-15=0;

11-13-14=0;

6-11-10-13=20;

-10-13+2,5-14+15-15=5;

5-12+15-15=70. Решая полученную систему уравнений, будем иметь: 11=5 А; 12=8 А; 13=1 А;

14=- 6 А; 15=2 А, что соответствует показаниям приборов. Отрицательный знак для тока 14 означает, что истинное направление этого тока противоположно принятому.

Контрольные вопросы и задания

1. Сформулируйте первый и второй законы Кирхгофа. Чем отличается второй закон Кирхгофа от закона Ома для полной цепи?

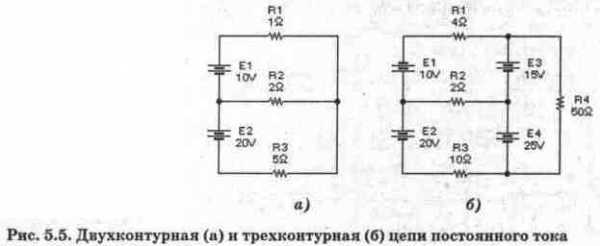
2. Проведите расчеты по определению токов в ветвях с использованием законов Кирхгофа для цепей на рис. 5.5. После подключения к схемам необходимых измерительных приборов проведите их моделирование. Сравните полученные данные с результатами расчетов.

riostat.ru