При каких параметрах цепи возникают резонанс тока и напряжения. В каких цепях и при каких условиях возникает резонанс напряжения

Резонанс напряжений и резонанс токов

В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.

Резонанс напряжений

Резонанс напряжений возникает в последовательной RLC-цепи.

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.

При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.

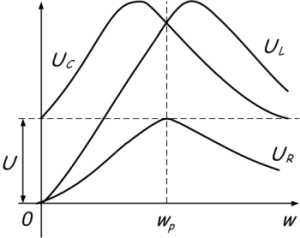
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

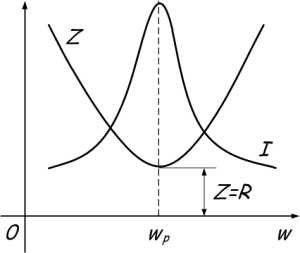
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.

Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.

Резонанс токов

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.

Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

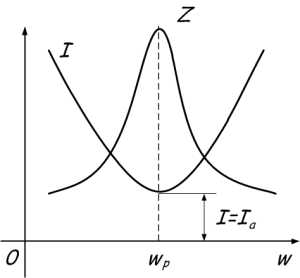
Выразим резонансную частоту

Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.

Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.

electroandi.ru

§56. Резонанс напряжений и резонанс токов

Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хси полное сопротивление Z становится равным активному сопротивлению R:

Z = ?( R2 + [?0L — 1/(?0C)]2 ) = R

В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.

Угловая частота ?0, при которой имеют место условия резонанса, определяется из равенства ?oL = 1/(?0С).

Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Отсюда имеем

?o = 1/?(LC) (74)

Если плавно изменять угловую частоту ? источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ?o), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ?oL = 1/(?oC). Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной частицепи при резонансе I=U?(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.

Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ?0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения

Рис. 197. Зависимость тока I и полного сопротивления Z от ? для последовательной (а) и параллельной (б) цепей переменного тока

Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов

в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.

Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1 и R2, будет равенство реактивных проводимостей BL = BC ветвей, в которые включены индуктивность и емкость.

Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.

Если в рассматриваемой параллельной цепи изменять частоту ?о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.

В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ?0.

Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.

electrono.ru

При каких параметрах цепи возникают резонанс тока и напряжения

В цепи переменного тока с активным сопротивлением, индуктивностью и емкостью, при их последовательным соединении, сила тока будет максимальной, ограниченной только активным сопротивлением. Поэтому при равенстве индуктивного и емкостного сопротивлений в последовательной цепи наступает - резонанс напряжений.

Резонанс напряжений в энергосистемах иногда возникает непредвиденно и приводит к тому, что на отдельных установках возникают перенапряжения, в несколько раз превышающие рабочие напряжения.

Явление резонанса состоит в том, что напряжение на индуктивности и напряжение на емкости, т.е. частичные напряжения в цепи, могут получить очень большие значения, во мгого раз превышающие напряжение источника тока. Если при этом активное сопротивление цепи невелико, то сила тока в цепи должна сильно возрасти и при отсутствии в цепи активного сопротивления, достаточно самого небольшого напряжения, чтобы в случае резонанса вызвть ток, бесконечно большой силы. При этом вполне очевидно, что угол сдвига фаз равно нулю. . Таким образом электрическая цепь при резонансе напряжений, вследствие взаимокомпенсации индуктивных и емкостных сопротивлений, ведет себя по отношению к внешней ЭДС, как чисто активное сопротивление.

При параллельном соединении активного, индуктивного и емкостного сопротивлений и отсутствии сдвига фаз между током и напряжением на зажимах цепи наступает резонанс токов. Т.е. при равенстве индуктивного и емкостного сопротивлений в цепи параллельного включения их с активным ток в цепи достигает своего минимального значения.

Явление резонанса токов наступает вследствие взаимокомпенсации индуктивных и емкостных проводимостей, а потому электрическая цепь в этом случае ведет себя по отношению к внешней ЭДС, как чисто активная проводимость, следовательно, угол сдвига фаз в главной цепи при резонансе токов равен нулю.

Следует отметить, что при резонансе токов возможны случаи, когда токи в индуктивной катушке и в конденсаторе могут превосходить, и иногда намного, суммарный ток в цепи. При резонансе токов энергия магнитного поля индуктивности переходит в энергию электрического поля конденсатора и наоборот, а энергия от источника расходуется только в активных сопротивлениях.

www.eti.su

Резонанс токов

Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. BL=BC.

Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Данная схема соответствует цепи, представленной на рис. 8, а, для которойR2 = 0, а R1=Rк (здесьRк – активное сопротивление катушки индуктивности). Полная проводимость такой цепиY=.

Условие резонанса токов (BL=BC) можно записать через соответствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивлениеRк, определяется выражениемBL=XL/=L/(Rк2+2L2), а проводимость конденсатора без учета его активного сопротивления (RC= 0)BC=XC/= 1/XC=C, то условие резонанса может быть записано в виде

L/(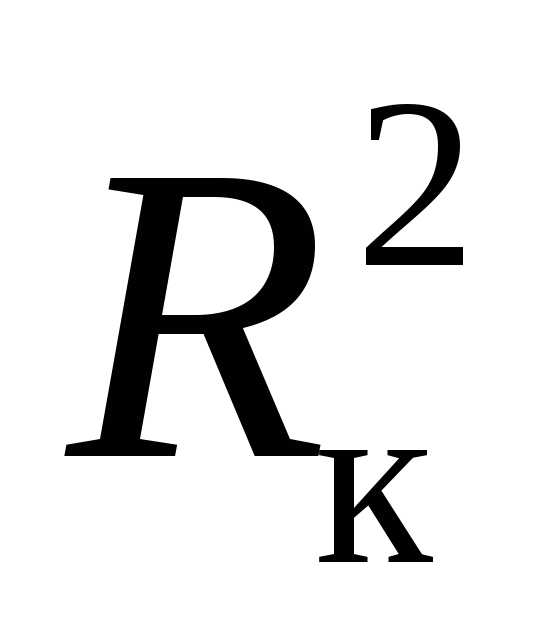+2L2) = C.

Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров Rк,L,Cипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров.

Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.

В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L, путем изменения емкостиСбатареи конденсаторов. С изменением емкостной проводимостиBC=C, пропорциональной емкости конденсатора, происходит изменение полной проводимостиY, общего токаIи коэффициента мощности cos. Указанные зависимости приведены на рис. 10,a. Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (BL=BC) своего минимума, а затем возрастает с увеличениемС, в пределе стремясь к бесконечности. Общий токI=YU, потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости.

Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G/Y. В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями.

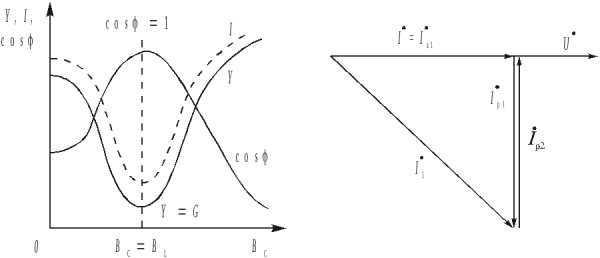
a)б)

Рис. 10

1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей:

Y = =G.

2. Минимальное значение проводимости обусловливает минимальное значение тока цепи:

I = YU = GU.

3. Емкостный ток ICи индуктивная составляющаяIL тока катушкиIкоказываются при этом равными по величине, а активная составляющая тока катушкиIа1 становится равной токуI, потребляемому из сети:

Iр1 = IL = BLU = BCU = IC = Iр2; Iа = Iа1 =GU = YU =I.

При этом реактивные составляющие токов IL иICв зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI, потребляемый электрической цепью из сети.

4. Реактивная составляющая полной мощности цепи при BL=BCоказывается равной нулю:

Q = BLU2  BCU2 = QL  QC = 0.

При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу.

5. Полная мощность цепи при резонансе равна ее активной составляющей:

S = YU 2 = GU 2 = P.

6. Коэффициент мощности всей цепи при резонансе:

cos = P/S = GU 2/YU 2 = 1.

Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б. В табл. 2 методических указаний по выполнению работы обозначениямIL, IK, IC соответствуют обозначенияIр1, I1, Iр2 на векторной диаграмме токов (рис. 10,б).

Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность. К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах.

studfiles.net

Вопрос10. Какую опасность для электрических устройств представляет резонанс напряжений? Где используется резонанс напряжений?

Ответ10. При резонансе, напряжения на емкости и на индуктивности равны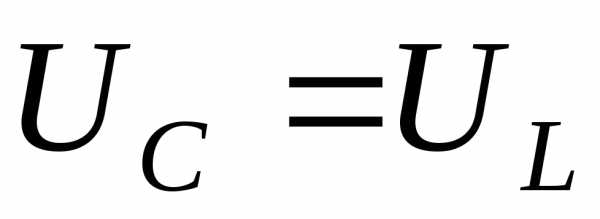и могут значительно превышать подводимое напряжениеU, есл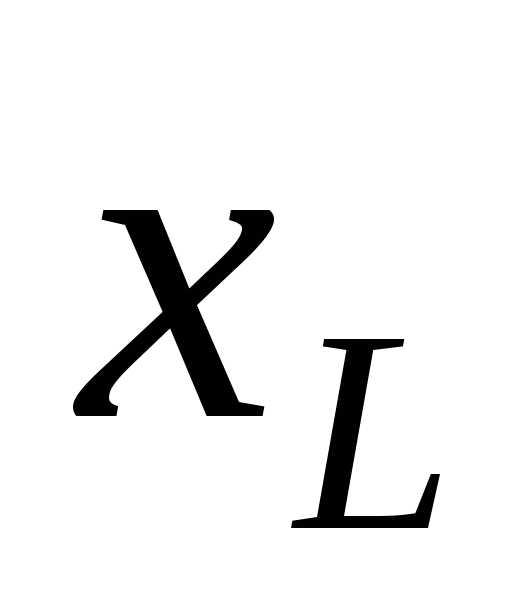ии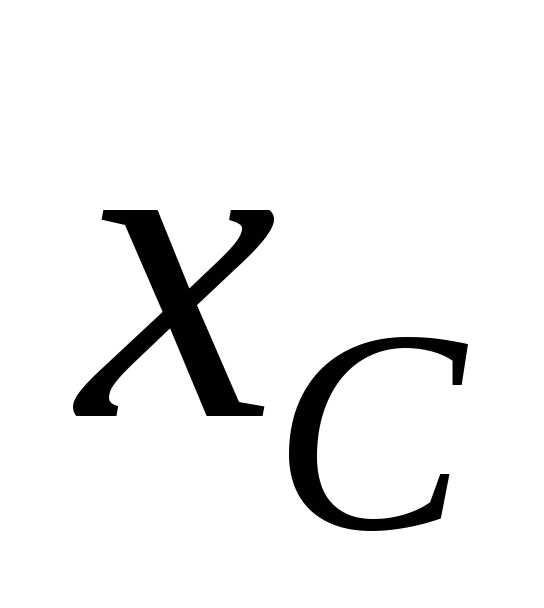значительно превышаютR:

, .

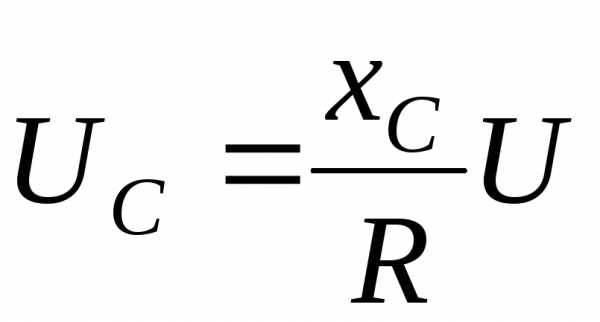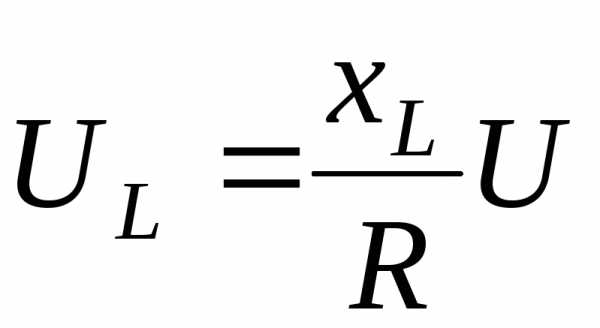Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробоя изоляции.

В тоже время, резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике в различных приборах и устройствах, основанных на резонансных явлениях. Радиоприемники настраиваются на волну( частоту) радиостанции путем изменения емкости. При резонансе, частота передающей станции и частота контура LCсовпадают, что приводит к значительному усилению только этого сигнала на входе приемника. ОтношениеXC/Rможет достигать 104, поэтому напряжение на емкостиUCбудет больше входного сигнала антенныUво столько же раз.

Тема №3. ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ ФАЗ НАГРУЗКИ «ЗВЕЗДОЙ»

Цель работы: 1) ознакомиться с трехфазной цепью переменного тока и ее основными режимами работы при соединении фаз приемника «звездой»

2) по опытным данным выяснить влияние нейтрального провода на работу трехфазной цепи;

3) усвоить методику построения векторных диаграмм для основных режимов работы;

4) изучить способы измерения напряжений, токов и активной мощности цепи.

Приборы и оборудование

Исследование трехфазной цепи проводится на универсальном стенде, где имеется нагрузка в виде трех ламповых реостатов (активная нагрузка). Для измерения величины токов и напряжений используются амперметр PA1 и вольтметрPV1 с вилками. При включении амперметраPA1 в гнезда соответствующей фазы тумблер, замыкающий эти гнезда, на время измерения ставится в положение «отключено» (SA3 для фазыa,SA5 для фазыbиSA7 для фазыc). С помощью двухэлементного ваттметраPW1 иPW2 измеряется активная мощность при трехпроводной системе.

Контрольные вопросы

Вопрос1. Как обозначаются зажимы трехфазного источника и приемника?

Ответ1. Большими буквами А,В,С и X,Y,Z обозначают начала и концы обмоток генератора. Концы и начала сопротивлений нагрузки обозначают малыми буквами a,b,с и x,y,z соответственно.

Вопрос2.Как соединяются электроприемники «звездой»?

Ответ2. Существуют 2 варианта соединения приемника и генератора по схеме звезда: а) трехпроводная и б) 4-х проводная или схема соединения с нейтральным проводом.

Для соединения фаз приемника «звездой» без нейтрального провода концы сопротивлений фаз приемника (x,y,z) соединяют в одну общую точкуn, называемую нулевой, или нейтральной точкой приемника (рис. 5а), начала фаз приемника (a,b,c) присоединяют к проводам, идущим к соответствующим фазам генератора (A,B,C). Эти провода называются линейными.

Для соединения фаз приемника «звездой» с нейтральном проводом, к предыдущей схеме добавляют провод, соединяющий нейтральную точку нагрузки nи нейтральную точку генератораN (рис.5б). Этот провод называютнейтральным.

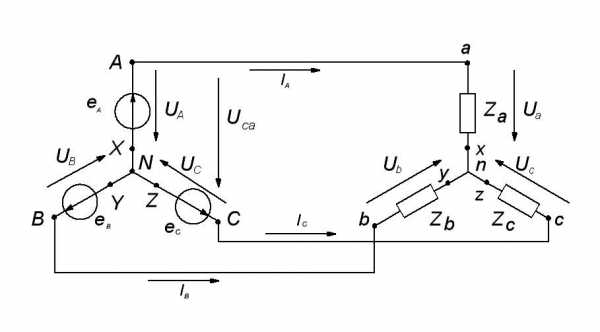
Рис. 5а

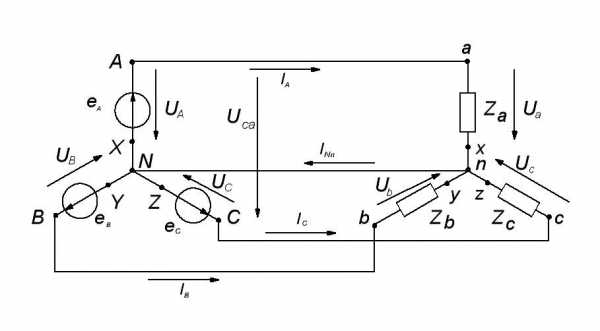
Рис. 5б

studfiles.net

Резонансные режимы в цепи. Резонанс напряжения, резонанс

Токов. Частотные характеристики резонансных цепей

Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Поэтому возможны такие сочетания этих элементов, когда входное реактивное сопротивление или входная реактивная проводимость всей цепи равны нулю. При этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи называются резонансными.

Резонанс напряжений. На рис.2.7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (рис.2.10). Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения.

Ток в резонансном режиме достигает максимума, так как полное сопротивление zцепи имеет минимальное значение:

Условие возникновения резонанса: .

Частоту называют резонансной частотой:

. (2.46)

Из (2.46) следует, что режима резонанса можно добиться следующими способами:

1) изменением частоты;

2) изменением индуктивности;

3) изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, значительно превышающие напряжение на входе цепи, если реактивные сопротивления значительно превышают активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости:

Отношение Q называют добротностью контура.

Добротность показывает, во сколько раз напряжения на реактивных элементах превышают входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные свойства характеризуют также величиной обратной добротности , называемой затуханием контура.

Волновое сопротивление контура или характеристическое сопротивление определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:

При резонансе напряжений малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Покажем, что при резонансе в любой момент времени суммарная энергия магнитного и электрического полей остается постоянной:

. (2.47)

Пусть ток в резонансном контуре , тогда напряжение на емкости отстает по фазе от тока на 900 .

Суммарная энергия магнитного и электрического полей (2.47) равна:

При резонансе

, .

Следовательно, const.

Если в схеме (рис.2.10) величина ЭДС и параметры R, L, C неизменны, но меняется частота , то изменяется реактивное сопротивление X и, следовательно, полное сопротивление угол . Зависимости параметров двухполюсника (действительной и мнимой части входного сопротивления или входной проводимости) от частоты называют частотными характеристиками.

Реактивное сопротивление

при трех характерных значениях частоты принимает предельные значения, равные нулю, либо бесконечности (рис.2.21).

При , при , при имеет место резонанс напряжений и X=0. Аргумент функции, при котором она принимает бесконечное значение, называется полюсом функции, а аргумент, при котором она принимает нулевое значение, называется нулевым значением. Отметим, что в момент резонанса происходит изменение характера реактивного сопротивления: при реактивное сопротивление имеет емкостной характер, а при - индуктивный характер.

Рис. 2.21

Величина действующего тока в цепи и напряжения на индуктивности и емкости также зависят от изменения частоты:

Зависимости действующих значений тока и напряжений на элементах цепи при изменении частоты называют резонансными кривыми. Резонансные характеристики , , приведены на рис.2.23.

Напряжение на емкости при стремится к U, а при стремится к нулевому значению, напряжение на индуктивности при равно нулю, при стремится к U. При резонансной частоте и взаимно компенсируются, ток цепи максимален, напряжение источника приложено к активному сопротивлению.

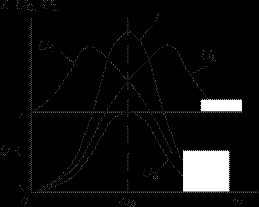
Рис. 2.22

Из рис. 2.22 видно, что максимум напряжения на индуктивности и максимум напряжения на емкости имеют место при частотах не равных резонансной частоте. Максимум имеет место при частоте меньшей , а максимум при частоте большей .

В электроэнергетических устройствах влияние резонанса, как правило, нежелательное, так как при резонансе напряжения на индуктивных и емкостных элементах могут значительно превышать номинальные значения. Такие явления могут возникать при подключении к зажимам синхронного генератора или трансформатора длинной линии передачи или кабеля, не замкнутых на приемник нагрузки. Генератор и трансформатор имеют индуктивное сопротивление, а линия или кабель обладают емкостью и индуктивностью. При отсутствии нагрузки на конце линии затухание такой цепи очень мало и возникают перенапряжения, если частота близка к резонансной.

Явление резонанса напряжений широко используется в радиопередающих и радиоприемных устройствах.

Резонанс токов. На рис.2.11 приведена цепь, включающая параллельно соединенные активное сопротивление, идеальная индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи (рис.2.14). При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов.

Из условия возникновения резонанса тока получим формулу для резонансной частоты тока:

Полученное выражение для резонансной частоты совпадает с (2.46). Резонанса токов можно добиться изменением частоты, изменением индуктивности либо емкости.

В режиме резонанса тока полная (входная) проводимость цепи - минимальна, а полное сопротивление - максимально. Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение. В идеализированном случае при R = 0,

и .

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.

При резонансе токов возможны режимы, когда токи через индуктивность и емкость значительно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии

Величина имеет размер проводимости и называется волновой проводимостью контура.

Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности и емкости над током в неразветвленной части схемы :

Величина обратная добротности является затуханием контура.

Энергетические процессы при резонансе токов аналогичны энергетическим процессам при резонансе напряжений. Малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Суммарная энергия магнитного и электрического полей при резонансе токов также в любой момент времени остается постоянной.

Частотные характеристики проводимостей ветвей с индуктивностью , с емкостью и входной проводимости приведены на рис. 2.23.

Рис. 2.23

При , при , при имеет место резонанс токов и b=0. В момент резонанса происходит изменение характера входной проводимости: при входная проводимость имеет индуктивный характер, а при - емкостной характер.

Резонансные характеристики , , при неизменном входном токе (I = const) и неизменных величинах активного сопротивления, индуктивности и емкости (R = const, L=const, C = const) определяются выражениями

, ,

и приведены на рис. 2.24.

При сопротивление индуктивности равно нулю и весь ток протекает через катушку , . При сопротивление конденсатора стремится к нулю и ток проходит только через конденсатор , . При частоте резонанса , токи в индуктивности и конденсаторе взаимно компенсируются, входной ток равен току через активное сопротивление . Максимумы токов через индуктивность и емкость не совпадают с максимумом напряжения при резонансной частоте . Максимум имеет место при частоте меньшей , а максимум при частоте большей .

Рис. 2.24

В энергетике процесс уменьшения угла сдвига фаз между напряжением на приемнике и током, потребляемым из сети, называют компенсацией угла сдвига фаз. Входное сопротивление большинства промышленных предприятий имеет индуктивный характер вследствие массового использования асинхронных двигателей. Для уменьшения величины потребляемого тока за счет компенсации его реактивной составляющей и соответственно потерь электроэнергии в сети, параллельно приемнику энергии включают батареи конденсаторов. Экономически выгодно подключать конденсаторы на возможно более высокое напряжение, так как ток через конденсаторы пропорционален напряжению . Компенсация угла сдвига фаз обычно выполняется до значения коэффициента мощности cos = 0,9 0,95.

infopedia.su

Контрольные вопросы

1. Записать выражение закона Ома для цепи с последовательным соединением конденсатора и индуктивной катушки. Чему равны полное сопротивление цепи и коэффициент мощности cos ?

I=U/Z

Коэффициент мощности cosφ при резонансе напряжений равен единице.

Cosφ=P/s= UR/U

2. Условие, признак и применение резонанса напряжений. В каком случае резонанс напряжений вреден? Почему?

Режим, при котором в цепи с последовательным соединением индуктивного и емкостного элемента напряжение на входе совпадает по фазе с током, резонанс напряжения.

внезапное возникновение резонансного режима в цепях большой мощности может вызывать аварийные ситуацию, привести к пробою изоляции проводов и кабелей и создать опасность для персонала.

3. Какими способами можно достичь резонанса напряжений?

При подключении колебательного контура, состоящего из катушки индуктивности и конденсатора, к источнику энергии могут возникнуть резонансное явление. Возможны два основных типа резонанса: при последовательном соединение катушки и конденсатора- резонанс напряжений, при их параллельном соединении- резонансов токов.

4. Почему при резонансе напряжений U2>U1?

Где R – активное сопротивление

I – сила тока

XL – индуктивное сопротивление катушки

XC – емкостное сопротивление конденсатора

Z – полное сопротивление переменного тока

При резонансе: UL = UС,

Где UС – напряжение катушки,

UL – напряжение конденсатора

Напряжение можно найти:

U=UR+UL+UC =>U=UR,

Где UR – напряжение катушки, к которой подключен вольтметр V2, значит напряжение V2=V1

5. Какова особенность резонанса напряжений? Объяснить ее.

Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки L, емкости конденсата С или частоты входного напряжения ω.

6. Записать выражение закона Ома через проводимости для цепи с параллельным соединением конденсатора и индуктивной катушки. Чему равна полная проводимость?

Закон Ома через проводимости для цепи переменного тока с параллельным соединение ветвей.

7. Условие, признак и применение резонанса токов.

т.е равенство индуктивной и емкостной проводимостей.

8. Какими способами можно достичь резонанса токов?

Режим, при котором в цепи, содержащей параллельное ветви с индуктивным и емкостным элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением , резонансом токов.

9. Почему при резонансе токов I2>I1?

Потому что, исходя из векторной диаграммы токов при резонансе график будет представлять собой прямоугольный треугольник, где токи I и I1 будут являться катетами, а ток I2 – гипотенузой. Следовательно, и I2 будет больше чем I1.

10. Какова особенность резонанса токов? Объяснить ее.

При резонансе токов токи в ветвях значительно больше тока неразветвленной части цепи. Это свойство-усилие тока- является важнейшей особенностью резонанса токов.

11. Объяснить построение векторных диаграмм.

Целью ее построения является определение активной и реактивной составляющих напряжения на катушке и угла сдвига фаз между напряжением на входе цепи и током

Расчеты

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. - B 3-х кн.: кн.1 /В. Г. Герасимов и др.; Под ред. В. Г. Герасимова. М.: Энергоатомиздат, 1996. – 288 с.
Касаткин А. С., Немцов М. В. Электротехника. М.: Высш. шк., 1999. – 542 с.
Электротехника /Под ред. Ю. Л. Хотунцева. М.: АГАР, 1998. – 332с.
Борисов Ю. М., Липатов Д. Н., Зорин Ю. Н. Электротехника. Энергоатомиздат, 1985. – 550 с.
ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. М.: Издательство стандартов, 1974.
ГОСТ 2.710-81 ЕСКД. Обозначения буквенно-цифренные в электрических схемах.

studfiles.net