ул.Симферопольская
дом 5, офис 9
![]() Корзина
Корзина
Корзина пуста
Вопрос №2. Параллельное соединение приемников в однофазных цепях (10 мин.). Резонанса напряжений условие
условия возникновения, резонансная частота, волновое сопротивление, добротность, векторная диаграмма.
Резонанс напряжений наблюдается в последовательных цепях. Рассмотрим режим резонанса напряжений для последовательной RLC-цепи.
Для схемы на рис. 4.1 справедливо
. (4.1)
Изменим частоту генератора или параметры катушки индуктивности или емкости так, чтобы для этой схемы было , тогданапряжение на входе, т.е. ток и напряжение на входе совпадают по фазе. В цепи – режим резонанса:
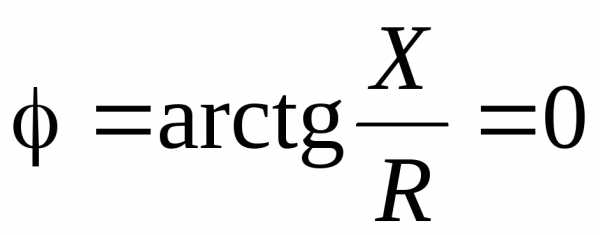 .
.
Частота, при которой наблюдается резонанс,  может быть определена из соотношения
может быть определена из соотношения
.
Ток в цепи в режиме резонанса
т.е. максимально возможный при данных параметрах контура.
Полная мощность цепи , т.е. равна мощности, выделяемой на активном сопротивлении.
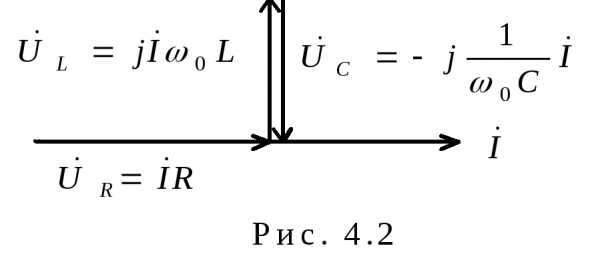
В каждый момент времени . Учитывая, что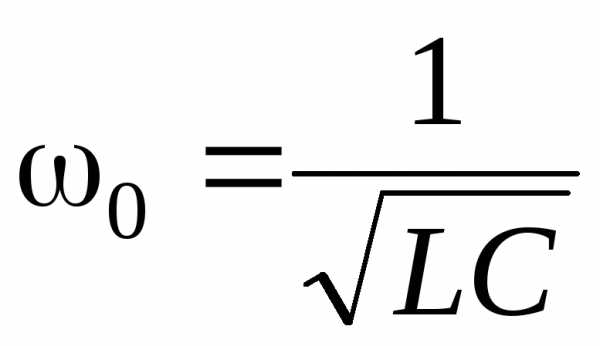 , получаем
, получаем
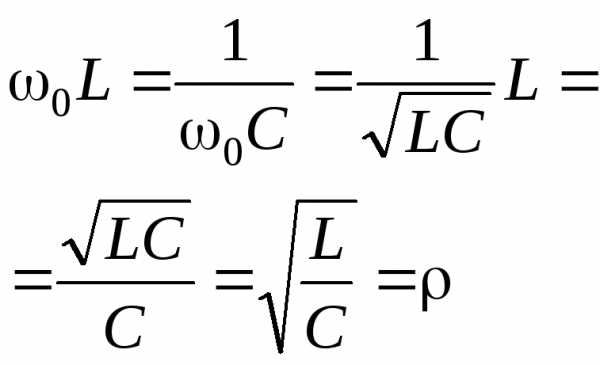
где – характеристическое, или волновое сопротивление резонансного контура, измеряемое в омах.
Отношение напряжения на реактивных элементах (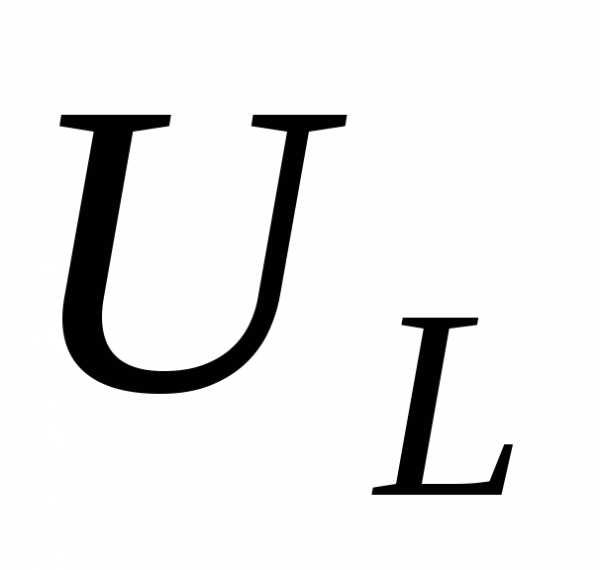 и
и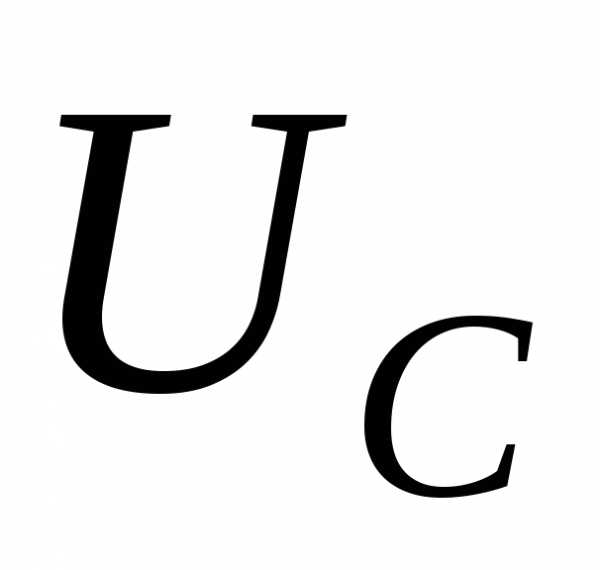 ) к напряжению на входе в режиме резонанса называютдобротностью контура:
) к напряжению на входе в режиме резонанса называютдобротностью контура:
. (4.5)
Чем больше 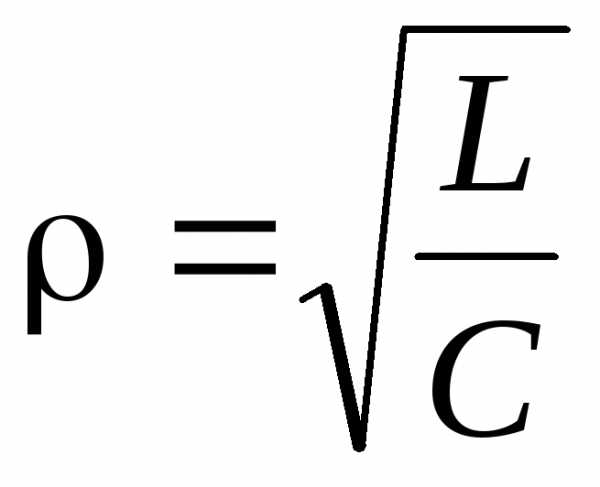 и чем меньше активное сопротивление в цепи, тем выше напряжение на реактивных элементах по сравнению с напряжением на входе контура.
и чем меньше активное сопротивление в цепи, тем выше напряжение на реактивных элементах по сравнению с напряжением на входе контура.
44) Частотные характеристики и резонансные кривые последовательного резонансного контура.
Зависимости параметров контуров RLC-контура от частоты называют частотными характеристиками. Это индуктивное сопротивление , емкостное сопротивление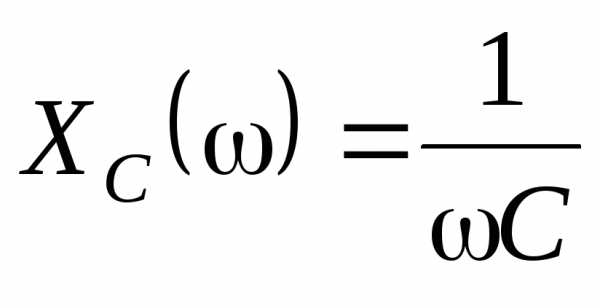
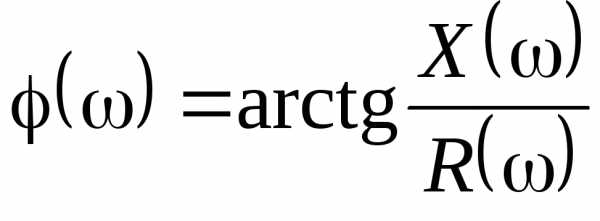 .
. В момент резонанса 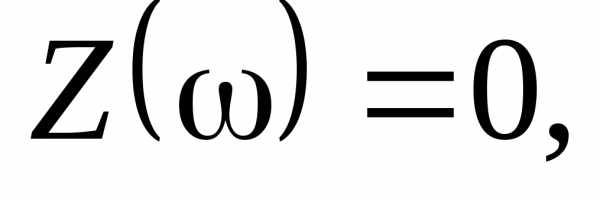
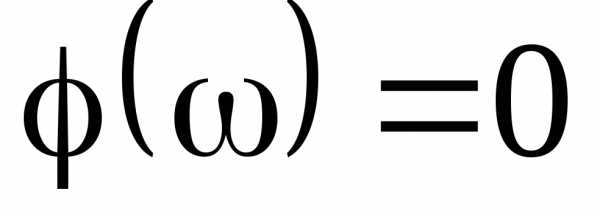 .
.
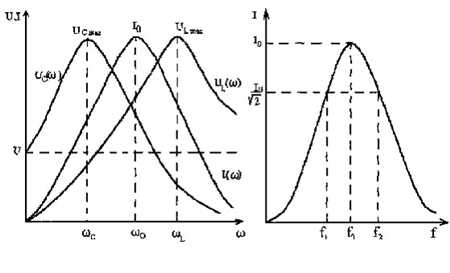
Зависимости тока I(), напряжения на индуктивности UL(), напряжения на емкости UC() называют резонансными характеристиками.
При добротности контура Q < 5 максимумы напряжений UL и UC смещаются друг от друга на одно и то же значение частоты от резонансной 0. При добротности контура Q >5 максимумы этих напряжений при резонансной част,оте = 0 сливаются.
45) Резонанс токов: условие возникновения, резонансная частота, волновая проводимость, добротность, векторная диаграмма. Контур с потерями.
Р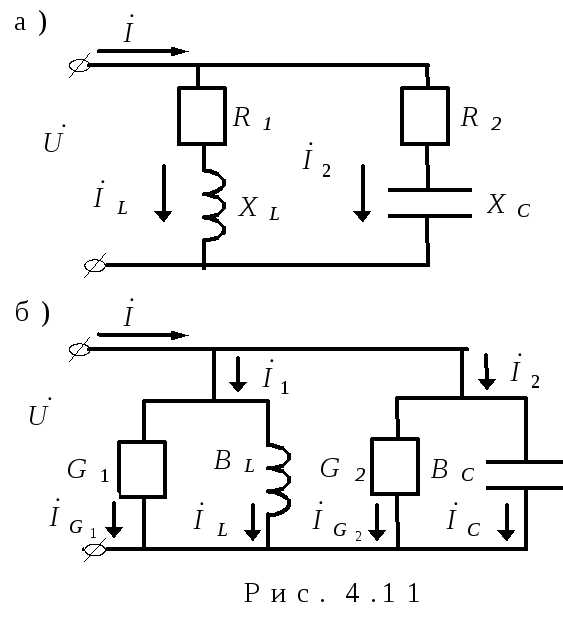 езонанс токов наблюдается в параллельных ветвях. При резонансе токов по фазе совпадают ток общей ветви и напряжение на параллельном участке. Рассмотрим резонанс токов в схеме с параллельными ветвямиRL и RC (рис. 4.11, а).
езонанс токов наблюдается в параллельных ветвях. При резонансе токов по фазе совпадают ток общей ветви и напряжение на параллельном участке. Рассмотрим резонанс токов в схеме с параллельными ветвямиRL и RC (рис. 4.11, а).
Заменим данную схему эквивалентной, приведенной на рис. 4.11, б.
В этой схеме приняты следующие обозначения:
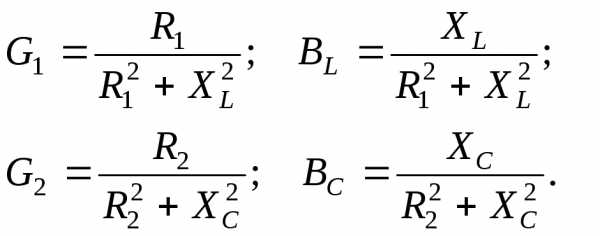 (4.8)
(4.8)
Для данной схемы справедливо
В режиме резонанса 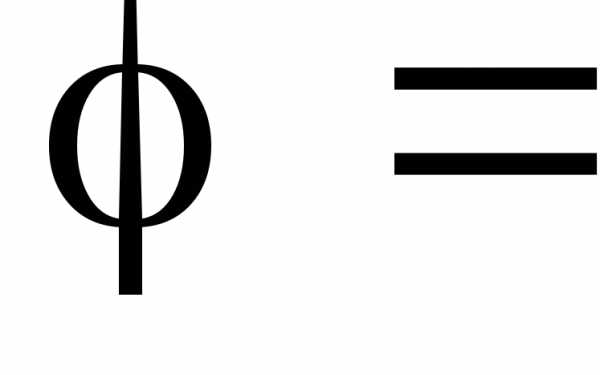
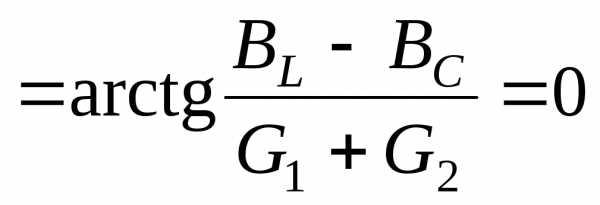 . Это возможно, если будет выполнено условие
. Это возможно, если будет выполнено условие
и соответственно
При резонансе полная мощность, которая потребляется контуром, минимальна и носит активный характер
.
В режиме резонанса ток на входе параллельного контура , т.е. минимальный ток для этой схемы при неизменном напряжении на входе. ПриG 0 I 0. Сопротивление такой цепи Z . Для резонансной частоты 0 такой контур принято называть фильтром - пробкой.
Величина резонансной частоты для приведенной схемы определяется из условия
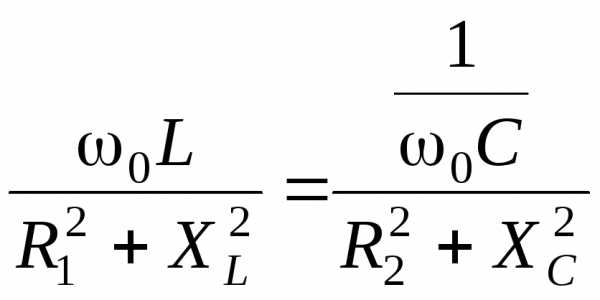 .
.
Приведя к общему знаменателю и умножив обе части на 0, после преобразований получим.
Резонанс в такой схеме может иметь место, если только выполняются следующие условия:
;
.
П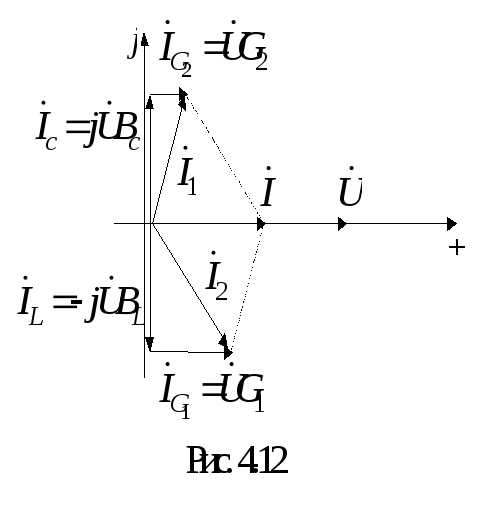 рисхема находится в резонансе при любых частотах. Это так называемыйвсеволновой резонанс.
рисхема находится в резонансе при любых частотах. Это так называемыйвсеволновой резонанс.
Основой для построения векторной диаграммы является описание схемы с помощью выражения (4.9). При построении совместим с вещественной осью напряжение , тогда векторная диаграмма будет иметь вид, представленный на рис. 4.12, если учесть, что.
Под добротностью контура при резонансе токов понимают отношение тока на реактивных элементах IL или IС к току на входе контура I
. (4.14)
При незначительных потерях в контуре токи IL и IC могут многократно превышать токи на входе схемы.
Вопрос №2. Параллельное соединение приемников в однофазных цепях (10 мин.)
Расчет цепи с параллельным соединением проводников (рис. 7,а) можно осуществить различными способами: методом векторных диаграмм, методом проводимостей и методом комплексных чисел. Первый метод не позволяет с большой точностью осуществить расчеты (рис. 7, б), поэтому были введены методы комплексных чисел и метод проводимостей. Рассмотрим метод проводимостей подробнее.
а) б)
Рис. 7. Схема разветвленной цепи и векторная диаграмма
резонанса напряжений
где g1, g2 – активные проводимости ветвей;
b1, b2 – реактивные проводимости ветвей.
Необходимо отметить, что знак реактивных проводимостей получается автоматически, т.к. ,. Т. к.XL2 и XC1 равны нулю, то b1>0, b2<0.
Общий ток
где – полная проводимость цепи, См.
Треугольник проводимостей представлен на рис. 8.
Рис. 8. Треугольники проводимостей
Функции угла φ определяют так:
;
Выражения для мощностей принимают такой вид:
;
Выводы по второму вопросу: таким образом, для расчета цепей с параллельным соединением приемников используются методы векторных диаграмм, проводимостей и комплексных чисел.
Вопрос №3. Резонанс напряжений и токов (20 мин.)
Резонансным режимом работы цепи – режим, при котором ее сопротивление является чисто активным.
Различают два основных режима: резонанс напряжений и резонанс токов.
3.1. Резонанс напряжений
Резонанс напряжений – это явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
Рис. 9. Схема последовательного колебательного контура
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как tgφ=X/R.
Условие резонанса
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение является формулой Томсона, определяющей зависимость собственной частоты колебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f0. Вследствие потери колебания в контуре будут затухать, время затухания зависит от значения возникших потерь.
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 10.
Признаки резонанса напряжений:
а) сопротивление цепи Z=R минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которой тем больше, чем меньше потери в цепи.
Рис. 10. Векторная диаграмма и резонансная
кривая последовательного контура
Характеристики резонанса:
1) Волновое сопротивление контура
2) Добротность контура
3) Резонансная кривая характеризует способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот (рис. 10, б).
4) Полное сопротивление цепи при резонансе
На рис. 11 показана зависимость реактивного сопротивления Х=ХL -Хс от частоты источника f. Анализ этого графика показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При частотах, близких к fo, реактивное сопротивление мало и ток контура велик.
Рис. 11
studfiles.net
Резонанс напряжений, условие возникновения
Явление резонанса электрических напряжений наблюдается в цепи последовательного колебательного контура, состоящего из емкости (конденсатора), индуктивности и резистора (сопротивления). Для обеспечения энергетической подпитки колебательного контура в последовательную цепь включается также источник электродвижущей силы Е. Источник вырабатывает переменное напряжение с частотой W. При резонансе ток, циркулирующий в последовательной цепи, должен совпадать по фазе с э.д.с. Е. Это обеспечивается, если общее сопротивление схемы Z = R+J(WL – 1/WС) будет лишь активным, т.е. Z=R. Равенство:
(L – 1/WС) = 0 (1),
является математическим условием резонанса в колебательном контуре. При этом величина тока в цепи составит I = E/R. Если преобразовать равенство (1), то получим:
WL = 1/WС.
В этом выражении W - является резонансной частотой контура.
Важно то, что в процессе резонанса напряжение на индуктивности равно напряжению на конденсаторе и составляет:
UL = U = WL * I = WLE/R
Общая сумма энергий в индуктивности и емкости (магнитного и электрического полей) постоянна. Это объясняется тем, что между этими полями происходит колебательный обмен энергиями. Суммарное ее количество в любой момент неизменно. При этом обмена энергией между ее источником Е и цепью не происходит. Вместо этого имеет место непрерывное преобразование одного вида энергии в другой.
Для колебательных контуров применятся термин добротность, которая показывает, как соотносятся напряжение на реактивном элемента (емкость или индуктивность) и входное напряжение контура. Добротность вычисляется по формуле:
Q = WL/R
Для идеальной последовательной цепи с нулевым активным сопротивлением возникновение резонанса сопровождается незатухающими колебаниями. На практике затухание колебаний компенсируется подпиткой контура от генератора колебаний с частотой резонанса.
Явление колебательного резонанса широко используется в радиоэлектронике. В частности, входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, изменяемая с помощью регулировки емкости конденсатора, совпадает с частотой сигнала радиостанции, которую необходимо принять.

В электроэнергетике возникновение резонанса напряжений вследствие сопутствующих ему перенапряжений чревато нежелательными последствиями. Например, в случае подключения к генератору или промежуточному трансформатору длинной кабельной линии (являющейся колебательным контуром с распределенной емкостью и индуктивностью), не соединенной на приемном конце с нагрузкой (это называется режимом холостого хода), весь контур может оказаться в резонансом состоянии. В такой ситуации напряжения, возникающие на некоторых участках цепи, могут оказаться выше расчетных. Это может грозить пробоем изоляции кабеля и выходом его из строя. Такая ситуация предотвращается применением вспомогательной нагрузки.
www.strodom.ru
Явление резонансов напряжений и токов в электроцепях и условия их возникновения
Любая электрическая цепь, содержащая элементы со свойствами индуктивности и ёмкости, может являться разновидностью колебательного контура – системы, в которой обязательно возникают незатухающие (в идеальном случае) колебания электроэнергии на частоте собственного резонанса. Определяют резонансную частоту параметры ёмкости – С и индуктивности – L. В общем случае, частота (F) описывается формулой:

Простейший контур
При подключении заряженного конденсатора к выводам катушки в последней возникает электродвижущая сила самоиндукции, начальный ток которой равен и противоположен по направлению току разряда. В течение разряда в катушке накапливается магнитная энергия, достигающая максимального значения, когда конденсатор полностью разряжается. Емкостное сопротивление при этом минимально, и катушка индуктивности накопленную энергию передаёт в конденсатор, далее начинается заряд напряжением противоположной полярности до момента полного преобразования магнитной энергии в ёмкость и последующей передачей обратно. При этих процессах токи, проходящие через конденсатор и индуктивность, больше тока всего контура, поэтому возникает резонанс токов.
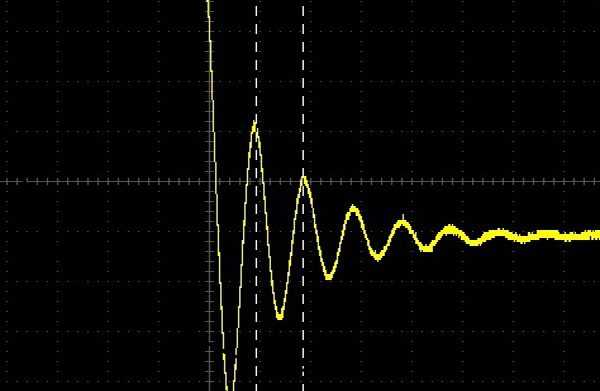
Подключение конденсатора к катушке
Затухание колебаний происходит вследствие потерь энергии в проводниках схемы и катушки, утечек в конденсаторе. Реальный колебательный контур, в котором присутствуют условия резонанса, всегда используется с внешним источником колебаний – генератором, сетью переменного тока, радиосигналом.
Резонанс токов
В случае параллельного подключения индуктивности, ёмкости и нагрузки к источнику переменного напряжения с частотой, равной резонансной контура, наблюдается значительное увеличение тока через элементы контура и возрастание его сопротивления.
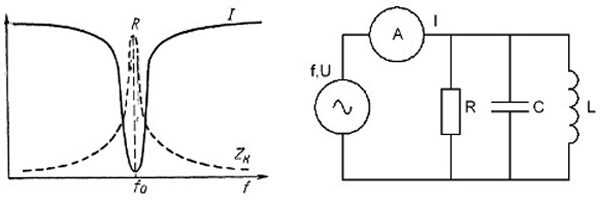
Параллельный контур
Свойства такого включения компонентов используются в заграждающих фильтрах различного назначения, пропускающих все частоты, кроме резонансной, при последовательном включении с сопротивлением нагрузки. При параллельном подключении контур не оказывает влияния на напряжение резонансной частоты. Если нагрузка обладает индуктивным сопротивлением, как асинхронный электродвигатель, то с параллельно включённым конденсатором они образуют колебательный контур. Если собственная его частота совпадает с частотой питающей сети, возрастает ток через нагрузку.
Резонанс напряжений
Подключение последовательного контура к генератору переменного напряжения частотой, равной собственной частоте контура, вызывает резонанс напряжений, при котором возрастают напряжения на индуктивности и ёмкости, с увеличением потребляемого тока от источника.
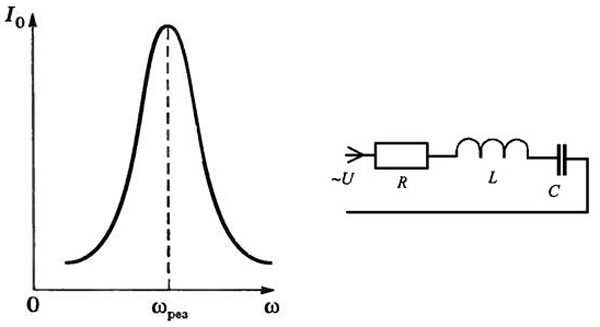
Последовательный контур
Сопротивление устройства на частоте резонанса минимально, что применяется в радиоприёмниках для настройки на частоту станции с помощью конденсатора переменной ёмкости. Как и при резонансе токов, последовательный контур применяется в фильтрах для подавления или пропускания определённых частот. В некоторых случаях возникновение резонанса напряжений приводят к нежелательным последствиям: кабель достаточной длины обладает значительной ёмкостью и индуктивностью и образует колебательный контур, при совпадении частоты сети и резонансной частоты кабеля возможен неконтролируемый рост напряжения с дальнейшим пробоем изоляции. В отдельных случаях последовательное включение конденсатора позволяет увеличить напряжение на индуктивной нагрузке – такая схема используется для запуска электродвигателей (пусковой конденсатор).
Условие резонанса любого типа возникает только при совпадении периодичности внешних воздействий с частотой собственных колебаний системы, на которую оказывается воздействие.
Явления резонанса применяются во множестве электронных и электротехнических устройствах. Магнетрон любой микроволновой печки – это резонатор, работающий как генератор колебаний СВЧ, феррорезонансный стабилизатор напряжения использует свойства параллельного колебательного контура.
Видео
Оцените статью:elquanta.ru
Условие резонанса напряжений
Поиск Лекций+: XL = XC
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XL = 1 Ом равно
+: Z = √5, φ = arctg1/2
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 2 Ом равно
+: Z = √13, φ = arctg2/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 1 Ом, XL = 2 Ом равно
+: Z = √5, φ = arctg2
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XL = 2 Ом равно
+: Z = 2√2, φ = arctg1
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XL = 3 Ом равно
+: Z = √13, φ = arctg3/2
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 3 Ом равно
+: Z = 5, φ = arctg3/4
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 4 Ом равно
+: Z = 5, φ = arctg4/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XL = 4 Ом равно
+: Z = √41, φ = arctg4/5
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 5 Ом равно
+: Z = √41, φ = arctg5/4
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XL = 5 Ом равно
+: Z = √61, φ = arctg5/6
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XL = 6 Ом равно
+: Z = √61, φ = arctg6/5
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XL = 7 Ом равно
+: Z = √85, φ = arctg7/6
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 2 Ом равно
+: Z = √20, φ = arctg1/2
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 5 Ом равно
+: Z = √41, φ = arctg5/4
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 1 Ом равно
+: Z = √17, φ = arctg1/4
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 1 Ом равно
+: Z = √10, φ = arctg1/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XL = 2 Ом равно
+: Z = √29, φ = arctg2/5
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XL = 2 Ом равно
+: Z = √40, φ = arctg2/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XL = 3 Ом равно
+: Z = √34, φ = arctg3/5
Модуль Z и фаза φ полного комплексного сопротивления при R = 1 Ом, XL = 7 Ом равно
+: Z = √50, φ = arctg7
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XC = 1 Ом равны
+: Z = √5, φ = arctg(-1/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 1 Ом, XC = 2 Ом равны
+: Z = √5, φ = arctg(-2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XC = 2 Ом равны
+: Z = √13, φ = arctg(-2/3)
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XC = 3 Ом равны
+: Z = √13, φ = arctg(-3/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 4Ом, XC =3 Ом равны
+: Z = 5, φ = arctg(-3/4)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XC = 4 Ом равны
+: Z = 5, φ = arctg(-4/3)
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XC = 4 Ом равны
+: Z = √41, φ = arctg(-4/5)
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XC = 5 Ом равны
+: Z = √50, φ = arctg(-1)
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XC = 5 Ом равны
+: Z = √61, φ = arctg-(5/6)
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XC = 6 Ом равны
+: Z = √61, φ = arctg(-6/5)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XC = 1 Ом равны
+: Z = √10, φ = arctg1/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 1 Ом, XC = 3 Ом равны
+: Z = √10, φ = arctg(-3)
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XC = 2 Ом равны
+: Z = 2√5, φ = arctg(-1/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XC = 4 Ом равны
+: Z = 2√5, φ = arctg(-2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XC = 2 Ом равны
+: Z = √39, φ = arctg(-2/5)
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XC = 5 Ом равны
+: Z = √39, φ = arctg(-5/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XC = 1 Ом равны
+: Z = √37, φ = arctg(-1/6)
Модуль Z и фаза φ полного комплексного сопротивления при R = 1 Ом, XC = 6 Ом равны
+: Z = √31, φ = arctg(-6)
Модуль Z и фаза φ полного комплексного сопротивления при R = 6 Ом, XC = 4 Ом равны
+: Z = √52, φ = arctg(-1/3)
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XC = 6 Ом равны
+: Z = √52, φ = arctg(-3/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 2 Ом, Xc = 1 Ом равны
+: Z = √10, φ = arctg1/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 3 Ом, Xc = 1 Ом равны
+: Z = 2√5, φ = arctg1/2
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 1 Ом, Xc = 3 Ом равны
+: Z = 2√5, φ = arctg(-1/2)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 1 Ом, Xc = 2 Ом равны
+: Z = √10, φ = arctg(-1/3)
Модуль Z и фаза φ полного комплексного сопротивления при R = 2 Ом, XL = 2 Ом, Xc = 1 Ом равны
+: Z = √5, φ = arctg1/2
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 3 Ом, Xc = 3 Ом равны
+: Z = 9, φ = arctg4/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 0 Ом, XL = 4 Ом, Xc = 3 Ом равны
+: Z = 1, φ = arctg1
Модуль Z и фаза φ полного комплексного сопротивления при R = 4 Ом, XL = 2 Ом, Xc = 5 Ом равны
+: Z = 5, φ = arctg(-3/4)
Модуль Z и фаза φ полного комплексного сопротивления при R = 3 Ом, XL = 5 Ом, Xc = 1 Ом равны
+: Z = 5, φ = arctg4/3
Модуль Z и фаза φ полного комплексного сопротивления при R = 5 Ом, XL = 2 Ом, Xc = 3 Ом равны
+: Z = √26, φ = arctg(-1/5)
Полное сопротивление пассивного двухполюсника Z при заданных действующих значениях напряжения U и тока I равно
+:
С увеличением частоты при неизменном действующем значении приложенного напряжения U действующее значение напряжения ###
+: увеличивается
Если известны полное сопротивление Z пассивного двухполюсника и угол φ сдвига фаз между напряжением u(t) и током i(t) на входе цепи, то комплексное сопротивление определяется выражением ###
+:
Комплексная амплитуда тока i(t)=1,41sin(314t -π/2) А составляет ###
+:
poisk-ru.ru
VI. Резонансные явления в электрических цепях Резонанс напряжений
Резонанс напряжений (или последовательный резонанс) может наблюдаться в электрической цепи, содержащей последовательно соединённые участки с разным характером реактивности. Название объясняется тем, что при резонансе оказываются равными друг другу по величине реактивные составляющие напряжений на указанных выше участках с разным характером реактивностей.
Резонанс напряжений может наблюдаться, к примеру, в цепи рис. 1.Найдём условие резонанса в этой цепи. Для этого участки R1 L и R2 C заменим эквивалентными (рис. 2).
Рис. 1
Как известно:
Если X’L окажется больше X’C, то цепь рис. 2 (а вместе с тем и цепь рис. 1) будет иметь активно-индуктивный характер и резонанс невозможен. Если X’L < X’C, то цепи рис. 1 и рис. 2 имеют активно-емкостной характер и резонанс также невозможен. При X’L = X’C цепи имеют чисто активный характер, следствием чего оказывается совпадение по фазе напряжения U и тока I, т.е. резонанс в цепи рис. 1.
Рис 2
С учётом (1) и (2) условие резонанса принимает вид:
Соотношение (3) приводит к уравнению третьей степени относительно частоты ω. Единственный положительный корень этого уравнения определяет так называемую резонансную частоту:
где – характеристическое сопротивление цепи.
Векторная диаграмма для цепи рис. 1 на резонансной частоте показана на рис. 3. Из диаграммы видно, что при резонансе, действительно, равны реактивные составляющие напряжений U1 и U2 .
U1p = U2p
Рис. 3
Рассмотрим интересный частный случай цепи рис. 1 при условии . Комплексное сопротивление такой цепи равно:
Таким образом, выяснилось, что комплексное сопротивление указанной цепи на всех частотах чисто активно. Это означает, что резонанс в данной цепи наблюдается на любой частоте.
Резонанс токов
Резонанс токов (или параллельный резонанс) может наблюдаться в электрической цепи, содержащей параллельно соединённые участки с разным характером реактивностей.
Название в этом случае объясняется тем, что при резонансе оказываются равными друг другу по величине реактивные составляющие токов указанных выше участков с разным характером реактивностей.
Резонанс токов может, к примеру, наблюдаться в цепи рис. 4
Условие резонанса для данной цепи можно найти аналогично тому, как это делалось для цепи рис. 1.
Рис. 4
Это условие имеет вид:
Решая это уравнение (5) относительно ω, найдём резонансную частоту:
Векторная диаграмма для цепи рис. 4 на резонансной частоте показана на рис. 5. Из неё видно, что при резонансе токов, действительно, равны по величине реактивные составляющие токов I1 и I2 .
I1p = I2p
Рис. 5
Точно так же, как и в предыдущем случае, можно доказать, что комплексное сопротивление цепи рис. 4 при условии
на любой частоте и равно: Z = R.
Это и означает, что и в этой цепи резонанс имеет место на всех частотах.
studfiles.net
Условие резонанса
Электроника Условие резонанса
просмотров - 808
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение является формулой Томсона, определяющей зависимость собственной частоты колебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f0. Вследствие потери колебания в контуре будут затухать, время затухания зависит от значения возникших потерь.
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 10.
Признаки резонанса напряжений:
а) сопротивление цепи Z=R минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которойтем больше, чем меньше потери в цепи.
Рис. 10. Векторная диаграмма и резонансная
кривая последовательного контура
Характеристики резонанса:
1) Волновое сопротивление контура
2) Добротность контура
3)Резонансная кривая характеризует способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот (рис. 10, б).
4) Полное сопротивление цепи при резонансе
На рис. 11 показана зависимость реактивного сопротивления Х=ХL -Хсот частоты источника f. Анализ этого графика показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При частотах, близких к fo, реактивное сопротивление мало и ток контура велик.
Рис. 11
Резонанс напряжений широко используется врадиотехнике и электронике для выделения сигналов заданной частоты.
Читайте также
При резонансе напряжений частота источника равна собственной частоте колебаний контура. Выражение является формулой Томсона, определяющей зависимость собственной частоты колебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура... [читать подробенее]
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭКСПЕРЕМЕНТА РЕЗОНАНС ТОКОВ Лабораторная работа №6 Цель работы: изучение условий возникновения резонанса токов в параллельных цепях, содержащих индуктивность и емкость, исследование влияния величины емкости на параметры... [читать подробенее]
oplib.ru